[will be published as: Dannenberg, R. B., Desain, P., & Honing, H. (1997). Programming language design for music. In G. De Poli, A. Picialli, S. T. Pope, & C. Roads (eds.), Musical Signal Processing. Lisse:Swets & Zeitlinger.]
Programming Language Design for Music
Roger B. Dannenberg, Peter Desain, and Henkjan Honing
Music invites formal description. There are many obvious numerical and structural relationships in music, and countless representations and formalisms have been developed. Computers are a great tool for this endeavor because of the precision they demand. A music formalism implemented as a computer program must be completely unambiguous, and implementing ideas on a computer often leads to greater understanding and new insights into the underlying domain.
Programming languages can be developed specifically for music. These languages strive to support common musical concepts such as time, simultaneous behavior, and expressive control. At the same time, languages try to avoid pre-empting decisions by composers, theorists, and performers, who use the language to express very personal concepts. This leads language designers to think of musical problems in very abstract, almost universal, terms.
In this chapter, we describe some of the general problems of music representation and music languages and describe several solutions that have been developed. The next section introduces a set of abstract concepts in musical terms. The following section, "computing with music representations," describes a number of computational issues related to music. Then, we begin to describe two languages we have developed that address these issues; the section "shared framework of Nyquist and GTF" introduces several important ideas that are common to our work and that of others. "The Nyquist language" describes a language for sound synthesis and composition; and "the GTF representation language" presents a music language emphasizing combination and transformation. The final section treats a number of implementation issues for music languages.
Representing Music
The domain of music is full of wonderfully complex concepts whose precise meaning depends on the context of their use, their user (be it composer, performer, or musicologist), and the time in history of their usage. It is difficult to capture these meanings in clear, formal representations that can be treated mechanically, but still reflect as much as possible of the richness of the domain constructs and their interplay. Studying prototypical examples of musical concepts and their natural, intuitive behavior is a good starting point for the recognition of the properties that representations for music should exhibit. Once representations can be designed that on the one hand do not reduce music to simplistic and rigid constructs, but on the other hand can be defined clearly and formally such that their behavior is predictable and easy to grasp, then their use in composition systems, analysis tools and computational models of music perception and production will be quite natural.
Continuous Versus Discrete Representations
One of the interesting representation problems in music is that musical information can be either discrete or continuous. Data is called discrete when it can take on a value or set of values that occur at some instant in time. For example, a musical note is often represented by a set of values for its attributes (pitch, loudness, instrument, duration, etc.) at a particular starting time. Data is said to be continuous if its value represents a function of time that has a well-defined value everywhere within some time interval or set of intervals. An example of this is a note whose pitch follows a contour evolving through time.
The distinction between continuous and discrete is not always clear-cut, and it may alternate between levels of representation; for example, a note may be represented by a discrete description at the specification level, a continuous audio signal at the realization level, and a discrete set of sample values at the signal-processing level. Sometimes the distinction is arbitrary. A trill, for example, can be described as one note with an alternating control function for its pitch, or it can be described as a discrete musical object consisting of several notes filling the duration of the trill. Both descriptions must add more elements (periods or notes) when stretched.
The Drum Roll or Vibrato Problem
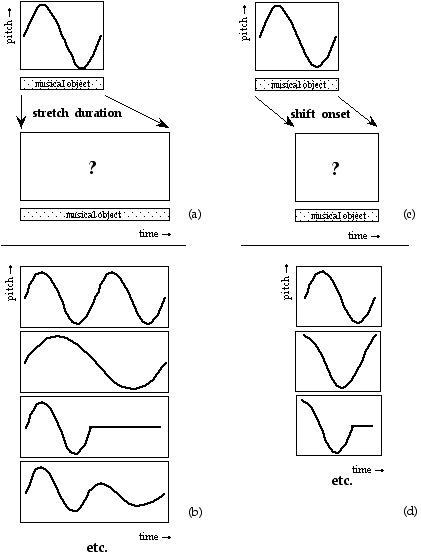
A well-known problem called the vibrato problem occurs when a representation of a musical note with a continuously variable pitch is transformed. In Figure 1a, such a continuous (control) function is shown. The difficulty is in how to obtain the proper shape or form of the pitch contour when it is used for a longer note, or, equivalently, when the note is stretched. In the case of its interpretation as an simple sinusoidal vibrato, some extra vibrato cycles should be added to the pitch envelope (see first frame in Figure 1b). When interpreted as an sinusoidal glissando, the pitch contour should be elasticity stretched (see second frame in Figure 1b). All kinds of intermediate and more complex behaviors should be expressible as well (see other examples in Figure 1b). A similar kind of control is needed with respect to the start time of a discrete object (see Figure 1c); what should happen to the contour when it is used for an object at a different point in time, or, equivalently, when the note is shifted? Again a whole range of possible behaviors can be thought of, depending on the interpretation of the control function&endash;the kind of musical knowledge it embodies. For instance, when multiple voices synchronize their vibrati, shifting a note may not alter the phase of the vibrato relative to global time.
insert Figure 1 around here
The drum roll problem is the discrete analog to the vibrato problem&endash;what happens when a drum roll is stretched? If the representation of the roll consists of audio samples, a simple resampling at a different rate will make the frequency spectrum lower and the drum strokes slower. If the roll is described in terms of drum stroke events only, each stroke can be easily made to sound roughly the same, but the strokes are slower. By convention, a stretched drum roll should maintain the same stroke rate and contain more strokes, so not only continuous data, like a vibrato control function, needs to embody musical knowledge, but also discrete musical objects, like a drum roll or a trill.
In more realistic situations, these continuous functions and discrete musical objects form layers of multiple, nested descriptions of continuous and discrete data (Honing 1993). For instance, Figure 2 illustrates the specification of an object with several of these alternating levels, and one can imagine that stretching such an object is not equivalent to simply stretching the resulting wave form. Instead, "to stretch" is some sort of abstract operation that involves more oscillations, changing amplitude contours, added cycles for the vibrati, and so on.
insert Figure 2 around here The Necessity of Planning and Anticipation
Traditional music is full of examples where a simple hierarchical structure is not rich enough to give a full account of performance behavior. Ornaments which precede the starting time of a structure are a good example. In order to play a note on a downbeat with an attached grace note, one must anticipate the starting time slightly to allow time for the grace note.
In order for humans to perform ornaments and transitions, there must be some amount of anticipation and planning. At any given time, the actions are at least partly a function of what is coming next. Most computer systems make the simplifying assumption that processing for an event at time t can begin at time t. Since computers are often fast enough, usually this strategy works fine. However, the anticipation problem illustrates that processing must sometimes precede the starting time, i.e., it has to be anticipated.
Anticipation is necessary in other contexts as well. In a music performance, a performer will alter the way a note ends and the way the next note begins depending upon overall phrase markings and the nature of the two notes. An instrumentalist may separate two notes with a very slight pause if there is a large leap in pitch, or a singer may perform a portamento from one note to the next and alter the pronunciation of phonemes depending upon neighboring sounds. The transition problem characterizes the need for language constructs that support this type of information flow between musical objects.
Many synthesizers implement a portamento feature. It enables glissandi between pitches to be produced on a keyboard. But the glide can only be started after its direction and amount is known, i.e. when a new key is pressed. This is different from, for instance, a singer who can anticipate and plan a portamento to land in time on the new pitch. Modeling the latter process faithfully can only be done when representations of musical data are, to a limited extent, accessible ahead of time to allow for this planning.
Even for a simple isolated note, the perceptual onset time may occur well after the actual (physical) onset. This is especially true if the note has a slow attack. To compensate, the note must be started early. Here again, some anticipation is required.
The Complex Nature of Structural Descriptions
Discrete structural descriptions in music form a rich class of constructs. Structural descriptions of various kinds (phrase, meter, voice, harmony, ornamentation, etc.) can be imagined that overlay the surface material (the notes) in an entangled, web-like way. Let us consider part-of relations, with which compound musical objects can be decomposed into their elements. Such a decomposition can take place on several levels, giving rise to nested structural units, for example, a hierarchy of phrases and sub-phrases. Sometimes these substructures behave almost homogeneously, at least for a portion of the hierarchy. Then the behavior at one level resembles behavior on a higher level closely and a recursive description is quite natural, for example, in defining the timing patterns linked to the levels of the metrical subdivision. Sometimes structural descriptions can be ambiguous, for instance, when different analyses of the same piece are available&endash;an ambiguity that may be kept intact and even communicated in a performance. Even more difficult to deal with formally are part-of relations that do not form a strict hierarchy, as is the case in two phrases that overlap, the end of the first being the beginning of the second. Part-of relations of various kinds are in general mutually incompatible, too&endash;a phrase may end in the middle of a bar.
Next to part-of relations, some parts can be considered more essential than others that are more of an ornamental nature. Some musicological analyses and, conversely, some regularities found in performance are based on ornamental distinctions. Another structural coupling between parts is the associative link between, for example, a theme and its variation.
There are other kinds of links than structural ones that can be made between concrete sets of events in a piece. Between abstract musical concepts&endash;such as between an A minor chord, a chord and a cluster&endash;there is a complex system of dependencies that can be modeled to a reasonable degree of accuracy with a set of is-a definitions and refinements thereof.
Context Dependency
Once musical structural descriptions are set up, the further specification of their attributes depends upon the context in which they are placed. Take for instance the loudness of a musical ensemble. The use of dynamics of an individual player cannot really be specified in isolation because the net result will depend on what the other players are doing as well. To give a more technical example, an audio compressor is a device that reduces the dynamic range of a signal by boosting low amplitude levels and cutting high amplitude levels. Now, imagine a software compressor operation that can transform the total amplitude of a set of notes, by adjusting their individual amplitude contours. This flow of information from parts to whole and back to parts is difficult to represent elegantly. We will refer to it as the compressor problem.
A comparable example is the intonation problem, where a similar type of communication is needed to describe how parallel voices (i.e., singers in a choir) adjust their intonation dynamically with respect to one another (Ashley 1992).
The Relation between Sounds and Instruments
Composers may think about notes as independent sounds or as directives for a single performer. In a pointillistic passage notes are distinct, and whether two notes emerge from the same clarinet or two is not important. The main entity here is the note. In contrast, a legato solo phrase of ten notes could not be played by ten violins, each playing one note. The main entity here is the solo violin. In most cases, composers think about both notes and instruments, and the existence of both entities is important. Thus, the note has dual nature; it is both an independent entity and an instrument control signal. The instrument problem refers to the challenge of modeling sound-producing resources (instruments) and their relationship to sound instances (notes).
The general problem is not restricted to a two-level hierarchy of notes and instruments. Consider that a violin note can be played on a choice of strings, and violins may be organized into sections. Other instruments also exhibit complex structures; a piano has a separate hammer for each string but a single damper pedal. A polyphonic synthesizer has a limited degree of polyphony, and modulation controls often apply to all notes. In the new physical modeling approach to sound synthesis (Smith 1992), finding general ways to represent these issues becomes a major challenge (Morrison and Adrien 1993).
Computing with Music Representations
We have presented a number of specific problems in music representation. In this section we will discuss how representations can be manipulated computationally, solving some of these problems. A few central constructs from computer science will turn out to be useful in describing the appropriate behavior.
Behavioral Abstraction or Context-sensitive Polymorphism
In order to get the desired isomorphism (strict correspondence) between the representation and the reality of musical sounds, a music representation language needs to support a property that we will call "context-sensitive polymorphism" or "behavioral abstraction" (we cannot agree on a single term). "Polymorph" refers to the fact that the result of an operation (like stretching) depends on its argument type, e.g., a vibrato time function behaves differently under a stretch transformation than a glissando time function. "Context-sensitive" indicates that an operation is also dependent on its lexical context. As an example of the latter, interpret the situation in Figure 1c as two notes that occur in parallel with one note starting a bit later than the other. The behavior of this musical object under transformation is now also dependent on whether a particular control function is linked to the object as a whole (i.e., to describe synchronized vibrati; see second frame in Figure 1d), or whether it is associated with the individual notes (e.g., an independent vibrato; see first frame in Figure 1d). Specific language constructs are needed to made a distinction between these different behaviors.
The term "behavioral abstraction" refers to the process of taking a specific behavior (anything that varies as a function of time) and abstracting it&endash;providing a single representation for a multitude of possible instances. An abstract behavior (such as vibrato) is abstract in two senses&endash;first, it regards certain properties as separate from the rest, e.g., the duration and starting time of vibrato may be considered to be particular details of vibrato. Second, a behavioral abstraction draws a distinction between a concept and any particular instance or realization.
Note that the vibrato problem is in fact a general issue in temporal knowledge representation&endash;an issue not restricted to music. In animation, for example, we could use similar representation formalisms. Think, for instance, of a scene in which a comic strip character walks from point A to point B in a particular way. When one wants to use this specific behavior for a walk over a longer distance, should the character make more steps (as in vibrato) or larger steps, or should it start running?
In-time, Out-of-time and Real-time
Music representations are intimately connected with time. Borrowing the terminology of Xenakis (1971), time-based computation can be in-time, meaning that computation proceeds in time order, or out-of-time, meaning that computation operates upon temporal representations, but not necessarily in time order. When in-time computations are performed fast enough, the program is said to be real-time&endash;the physical time delay in responding and communicating musical data has become so small that is not noticeable.
An example of in-time data is a MIDI data stream. Since MIDI messages represent events and state changes to be acted upon immediately, MIDI data does not contain time stamps, and MIDI data arrives in time order. When the computers, programs and synthesizers are fast enough (such that MIDI never overflows) a MIDI setup can be considered real-time. An example of out-of-time data is the MIDI representation used in a MIDI sequencer, which allows for data to be scrolled forward and backward in time and to be edited in an arbitrary time order.
"Out-of-time" languages are less restricted, hence more general, but "in-time" languages can potentially run in real time and sometimes require less space to run because information is processed or generated incrementally in time order.
Programs that execute strictly in time order are said to obey causality because there is never a need for knowledge of the future. This concept is especially important when modeling music perception processes and interactive systems that have to respond to some signal that is yet unknown&endash;for example, a machine for automatic accompaniment of live performance.
The situation may become quite complicated when there is out-of-time information about the future available from one source, whereas for the other source strict in-time processing is required, such as in a score-following application where the full score is known beforehand, but the performer’s timing and errors only become available at the time when they are made (Dannenberg 1989a).
Another confusing situation arises when a system designed or claimed to calculate in-time cannot run in real-time because of hardware limitations, and is developed using a simulation of its working by presenting its input out-of-time. Strict discipline of the developer is then needed to maintain causality and refrain from introducing any kind of "listen-ahead."
Discrete Representations
Discrete information comes in many forms. One of these is discrete data such as notes, which are often represented as a data structure with a start time and various attributes. Other sorts of discrete data include cue points, time signatures, music notation symbols, and aggregate structures such as note sequences. The term "discrete" can also be applied to actions and transitions.
A step or action taken in the execution of a program is discrete. In music-oriented languages, an instance of a procedure or function application is often associated with a particular time point, so, like discrete static data, a procedure invocation can consist of a set of values (parameters) and a starting time point. The use of procedure invocation to model discrete musical events is most effective for in-time computation, such as in real-time interactive music systems, or for algorithmic music generation. This representation is less effective for complex reasoning about music structures and their interrelationships, because these relationships may exist across time, while procedure invocation happens only at one particular instant.
Another sort of discrete action is the instantiation or termination of a process or other on-going computation. The distinction between discrete and continuous is often a matter of perspective. "Phone home" is a discrete command, but it gives rise to continuous action. Similarly, starting or stopping a process is discrete, but the process may generate continuous information.
Discrete data often takes the form of an object, especially in object-oriented programming languages. An object encapsulates some state (parameters, attributes, values) and offers a set of operations to access and change the state. Unlike procedure invocations, an object has some persistence over time. Typically, however, the state of the object does not change except in response to discrete operations.
Object-based representations are effective for out-of-time music processing because the state of objects persists across time. It is therefore possible to decouple the order of computation from the order of music time. For example, it is possible to adjust the durations of notes in a sequence to satisfy a constraint on overall duration.
Even within an object-based representation system, there is computation, and computation normally takes place in discrete steps, actions, or state transitions. Object updates, for example the so-called message passing of object-oriented programming languages, is another form of discrete event. Often, in music processing languages, object updates are associated with discrete time points, adding a temporal component to the operation.
As we have seen, the term "discrete" can apply to many things: data, program execution, state transitions, objects, and messages. It is helpful to have a generic term for all of these, so we will use the term discrete event or simply event when nothing more specific is intended.
Continuous Representations
Continuous data is used to represent audio signals, control information such as filter coefficients or amplitude envelopes, and other time-varying values such as tempo. Continuous data can be a "first-class" data type, an attachment to discrete data, or an even more restricted special type of data.
The most general possibility is to treat continuous data as a "first class" data type or class of object. For example, in the Nyquist language (which will be described in more detail below), continuous data is a data type that can be used for audio signals, control signals, or other time-varying values. In the GTF representation (see below), continuous data may exist as attachments to discrete structures at any level. Several language systems have been constructed where continuous functions serve strictly as transformations in time and in other controls. For example, tempo curves are continuous functions that provide a transformation from beat time to real time. Functions in Formula (Anderson and Kuivila 1986) provide tempo, duration, and other variables as a way to control expressive timing, articulation, and phrasing. The power of continuous representations is well illustrated by the fact that one composition system (Mathews and Moore 1970) embraced this format as its one and only representation of musical signals.
Anticipation
Representing transitions well is difficult because it requires that independent behaviors be joined in some way. FORMES (Cointe and Rodet 1984; Rodet and Cointe 1984) is perhaps the best example of a system that has specific mechanisms for transitions. In FORMES, a transition behavior is achieved by modifying the start and end times of the behaviors involved in the transition and interpolating between the behaviors. In FORMES, behaviors are implemented by objects organized in a tree structure, and the transition behavior requires several passes over the object tree, including some non-causal look-ahead. Language support for a more real-time "anticipation window" to support ornaments and transitions is an interesting area for future research.
With respect to ornaments, this is either non-causal (e.g., because we need to go back in time from the downbeat to the time of the grace note), or we need to complicate matters at some other level by designating the starting time of the pair of notes as before the downbeat. Many computer systems compute information with a time advance in order to achieve more accurate timing (Vercoe 1985; Anderson and Kuivila 1986) but it is unusual to allow observation of future events in order to modify current behavior (Loyall and Bates 1993).
Context Dependency
Why is modeling a compressor difficult? The problem is that a global amplitude function must depend upon local amplitude functions, and these local functions in turn depend upon starting times and durations (just as in the case of vibrato). It may not be possible to determine the amplitude of a note without instantiating the note in context, and even then, it may not be possible to identify and extract an envelope. Furthermore, in some languages, information can flow from a global function to a sequence of nested notes, but information cannot flow from a note attribute to a global function. (Note that this type of transformation can only be realized when musical objects are available after definition, e.g., when they are accessible data structures.)
One area where the distinction between causal and non-causal programming is the most obvious is the handling of duration. The problem with duration is that it is often nice to know in advance how long a note will last; the shape of the amplitude envelope, the exact frequency of vibrato, the dynamic level, and many other details may depend upon the length of a note. In a non-causal system, notes can be manipulated as abstract objects. For example, notes may be shifted, stretched and reorganized. After the organization is in place and durations are fixed, the details can be added with full knowledge of the note duration.
In the causal case, duration can be determined in various ways. In the simplest case, the duration may be specified at the time the note is started. This would be typical in a programming language where evaluation proceeds top-down from high-level procedures to the innermost low-level procedures. High-level procedures compute the details of each note including starting time, pitch, and duration. Even in this case, the duration of a phrase is the sum of the durations of its components, and all of these durations may not be known when the phrase begins.
Portamento is intimately connected to duration. Advanced knowledge of duration enables the anticipation of the ending time of a note, and anticipation allows the portamento to begin before the end of the note. Otherwise the portamento will be late.
Abstract Musical Structure vs. Instrument Structure
The resource-instance model (Dannenberg, Rubine, and Neuendorffer 1991) makes a distinction based on how discrete data or events are handled. In the first case, discrete information (either a data object or a function application as described above) denotes a new instance of some class of behaviors or objects. In the Music N family of languages (Mathews 1969) for example, each note in the score language denotes an instance (a copy) of an instrument computation described in the orchestra language.
In the second case, discrete information is directed to a resource (e.g., an instrument), where the information is used to modify the behavior of the resource. For example, a pitch-bend message in MIDI is directed to a channel resource, affecting the tuning of all notes sounding on that channel (either now or in the future).
A language or representation may be either instance-based, resource-based, or some combination of the two. In the combined case, discrete information is used to designate the instantiation (creation or allocation) of new resources. (This supports the instance model.) Once instantiated, a resource may receive updates that modify the behavior or instantiate sub-behaviors. (This supports the resource model.)
In the resource-instance model, one might create and play a virtual guitar by first instantiating a guitar resource. Next, updates are sent to this guitar resource, requesting the instantiation of six strings. Finally, updates are sent to stop the strings at particular frets and to strum the strings, making sound. The ability to instantiate new resources and to update the state of existing resources is very powerful because it provides a natural representation for addressing the instrument problem defined above.
The resource-instance model also provides flexibility. A composer can choose to instantiate a guitar for each note, to share the guitar but instantiate a new string for each note, or to play every note on the same string. These choices give rise to different sounds, and the model helps to clarify the available choices.
Structure
Music representations and languages support varying degrees and types of structure, ranging from unstructured (flat structure) note-lists to complex recursive hierarchical (tree-like) and heterarchical (many-rooted) structures.
Two-Level Structure
A simple two-level structure is found in the Music N languages such as Music V (Mathews 1969), Csound (Vercoe 1986), and cmusic (Moore 1990). In these languages, there is a "flat" unstructured list of notes expressed in the score language. Each note in the score language gives rise to an instance of an instrument, as defined in the orchestra language. Instruments are defined using a "flat" list of signal generating and processing operations. Thus, there is a one-level score description and a one-level instrument description, giving a total of two levels of structure in this class of language.
The Adagio language in the CMU MIDI Toolkit (Dannenberg 1986a, 1993a) and the score file representation used in the NeXT Music Kit (Jaffe and Boynton 1989) are other examples of one-level score languages. These languages are intended to be simple representations that can be read and written easily by humans and machines. When the lack of structure is a problem, it is common to use another programming language to generate the score. This same approach is common with the score languages in Music N systems.
Nested Discrete Structures
Rather than resort to yet another language to generate scores, it is possible to augment the score language with additional structure so that a separate language is not necessary. Typically, functions (or macros, or procedures) represent musical behaviors or collections of musical events. By invoking the function in multiple places, several instances of the behavior can be obtained, and by using nested functions, a hierarchical structure can be described. The section "shared framework of Nyquist and GTF" (below) will explore this idea further.
Recursive Structures
In addition to nested, hierarchical structures, languages can support true recursion. Consider the following prescription for a drum roll, "to play a drum roll, play a stroke, and if you are not finished, play a drum roll." This is a recursive definition because the definition of "drum roll" is defined using the "drum roll" concept itself. This definition makes perfectly good sense in spite of the circularity or recursion. Recursion is useful for expressing many structures.
Non-hierarchical structures
It is often not at all clear how specific knowledge about a particular kind of music should be represented, and "wiring-in" assumptions at a low level of the representation language can make it useless for applications for which the assumptions do not hold. When there is need for a general "part-of" relation between structural units, without the usual restriction to single strict hierarchical structure (e.g., representing overlapping phrases), it is important to represent this capability on a low level, with as little knowledge about music as possible, not relying on ad-hoc opinions about specific musical concepts. A solution that supports a general part-of relation with names that function as "hooks" to link in specific musical knowledge proved successful in POCO (Honing 1990), a workbench for research on expressive timing. Non-hierarchical structures are also found in representation work by Brinkman (1985) and Dannenberg (1986b).
Ornamental relations
Ornaments often have their specific behavior under transformation, e.g., a grace note does not have to be played longer when a piece is performed slower. In a calculus for expressive timing (Desain and Honing 1991) and in Expresso, a system based on that formalism (Honing 1992), ornamental structures of different kinds are formalized such that they maintain consistency automatically under transformations of expression (for instance, lowering the tempo or exaggerating the depth of a rubato). In this application one cannot avoid incorporating some musical knowledge about these ornaments and one has to introduce, for example, the basic distinction between acciacatura and appogiatura. (time-taking and timeless ornaments).
Shared Framework of Nyquist and GTF
We can now present more concrete proposals for representation and programming languages for music that are aimed at addressing the issues introduced above. One formalism (referred to as ACF, for "Artic, Canon and Fugue") evolved in a family of composition languages (in historic order, Arctic, Canon, Fugue, and Nyquist&endash;Dannenberg 1984; Dannenberg, McAvinney and Rubine 1986; Dannenberg 1989b; Dannenberg and Fraley 1989; Dannenberg, Fraley, and Velikonja 1991, 1992; Dannenberg 1992b, 1993b) and found its final form (to date) in the Nyquist system. The second formalism (called GTF, for "Generalized Time Functions") originated from the need to augment a composition system with continuous control (Desain and Honing 1988; Desain and Honing 1992a; Desain and Honing 1993). Their similarities and differences were discussed in Dannenberg (1992a) and Honing (1995). Here we will first describe the set of musical objects, time functions and their transformation that is shared by the ACF and GTF systems. We use the Canon syntax (Dannenberg 1989b) for simplicity. The examples will be presented with their graphical output shown as pitch-time diagrams.
In general, both the ACF and GTF systems provide a set of primitive musical objects (in ACF these are referred to as "behaviors") and ways of combining them into more complex ones. Examples of basic musical objects are the note construct, with parameters for duration, pitch, amplitude and other arbitrary attributes (that depend on the synthesis method that is used), and pause, a rest with duration as its only parameter. (Note that, in our example code, pitches are given as MIDI key numbers, duration in seconds, and amplitude on a 0-1 scale). These basic musical objects can be combined into compound musical objects using the time structuring constructs named seq (for sequential ordering) and sim (for simultaneous or parallel ordering). In Figure 3 some examples are given.
insert Figure 3 around here
New musical objects can be defined using the standard procedural abstraction (function definition) of the Lisp programming language, as in,
;; This is a comment in Lisp.
;; Define a function called "melody."(defun melody ()
;; that produces a sequence
;; of three sequential notes.;; note takes arguments pitch, dur, amp
(seq (note 60 .5 1)
(note 61 .5 1)
(note 62 .5 1)))
Figure 4 shows an example of the use of the melody abstraction, playing it twice sequentially.
insert Figure 4 around here
Both ACF and GTF provide a set of control functions or functions of time, and ways of combining them into more complex ones. We will give two examples of basic time functions: a linear interpolating ramp and an oscillator generating a sine wave.
There are several possible ways to pass time functions to musical objects. One method is to pass a function directly as an attribute of, for instance, the pitch parameter of a note (see Figure 5). When using this parameterization method for building complex musical objects, it has to be known in advance which parameters can be controlled from the outside&endash;he encapsulation of the musical object needs to be parameterized. For example, when building a chord function it may be parametrized naturally by the pitch contour of the root, but it has to be known in advance whether at some time in the future we will want to de-tune one specific note of the chord. Once foreseen, it is easy to write a chord function with an extra parameter for this capability, but in general it is hard to decide on the appropriate amount of encapsulation in defining compound musical objects for general use. (This is also one of the reasons why we believe in composition systems in the form of general programming languages with their capabilities of abstraction; there are so many styles of music composition that any pre-wired choice of the designer of a composition system is doomed to be wrong for some composer at some time.)
An alternative method to specification by parameterization is to make a musical object with simple default values and to obtain the desired result by transformation. For instance, a transposition transformation applied to a simple note with constant pitch yields a note with a specific pitch envelope. When using this method for specifying a complex musical object the transformation is in principle applied to the whole object and cannot differentiate its behavior with regard to specific parts.
insert Figure 5 around here
In one context the first method will be more appropriate, in another the latter. The following examples show the equivalence between specification by means of transformation and by parameterization (their output is as shown in Figure 5a and 5b, respectively):
;; specification by parameterization
(note (ramp 60 61) 1 1))
;; specification by transformation
(trans (ramp 0 1) (note 60 1 1))
;; specification by parameterization
(note (oscillator 61 1 1) 1 1))
;; specification by transformation
(trans (oscillator 0 1 1) (note 61 1 1))
Finally, both systems support different types of transformations. As an example of a time transformation, stretch will be used (see Figure 6a). This transformation scales the duration of a musical object (its second parameter) with a factor (its first parameter). As examples of attribute transformations we will use one for pitch (named trans), and one for amplitude (named loud). These transformations take constants (see Figure 6b, 6c and 6d) or time functions (see Figure 6e and 6f) as their first argument, and the object to be transformed as their second argument.
insert Figure 6 around here The Nyquist Language
Nyquist is a language for sound synthesis and composition. There are many approaches that offer computer support for these tasks, so we should begin by explaining some advantages of a language approach. A key problem in sound synthesis is to provide detailed control of the many parameters that are typically required by modern digital sound synthesis techniques. As described above, it is very difficult to anticipate the needs of composers; often, the composer wants to fix a set of parameters and focus on the control of a few others. A programming language is ideal for describing customized instruments that have only the parameters of interest and that behave according to the composer's requirements. In other words, the composer can create his or her own language that is specific to the compositional task at hand.
Composition itself can benefit from a programming language model. Musical information processing can range from the automation of simple mechanical tasks all the way to computer-based composition where all aspects of a composition are determined by a program. Whatever the approach, it is a great advantage to have a close link between the compositional language and the synthesis language. With Nyquist, one language serves both composition and signal processing, and blurs the distinction between these tasks.
Nyquist is based on Lisp, which has several advantages for music. First, Lisp is a very high-level language, with many built-in functions and data types. Second, Lisp is a good language for symbol processing, which is a common task when manipulating musical information. Finally, Lisp provides an incremental, interpreted programming environment which is ideal for experimental and exploratory programming.
Nyquist adds a few capabilities to Lisp to make it more suitable for sound synthesis and music composition. First, Nyquist adds a new data type called a SOUND, which efficiently represents audio and control signals. Second, Nyquist provides new control constructs that deal with time, including the sequential (seq) and parallel (sim) behaviors introduced above. Third, Nyquist supports various kinds of temporal and musical transformations such as transposition (trans), tempo change (stretch), and loudness (loud) control, that we defined above.
In the sections that follow, we will examine the new concepts and constructs that Nyquist adds to Lisp. It will be seen that a small number of new constructs are required to create a very flexible language for music.
The SOUND Data Type
A Nyquist SOUND is a time-varying signal. As is common in signal processing systems, the signal is represented by a sequence of samples denoting the value of the signal at regularly spaced instants in time. In addition to samples, a SOUND has a designated starting time and a fixed sample rate. Furthermore, a SOUND has a logical stop time, which indicates the starting time of the next sound in a sequence. (Sequences will be described later in greater detail.)
Multi-channel signals are represented in Nyquist by arrays of SOUNDs. For example, a stereo pair is represented by an array of two SOUNDs, where the first element is the left channel, and the second element is the right channel. Nyquist operators are defined to allow multi-channel signals in a straightforward way, so we will not dwell on the details. For the remainder of this introduction, we will describe SOUNDs and operations on them without describing the multi-channel case.
SOUNDs in Nyquist are immutable. That is, once created, a SOUND can never change. Rather than modify a SOUND, operators create and return new ones. This is consistent with the functional programming paradigm that Lisp supports. The functional programming paradigm and the immutable property of sounds is of central importance, so we will present some justifications and some implications of this aspect of Nyquist in the following paragraphs.
There are many advantages to this functional approach. First, no side-effects result from applying (or calling) functions. Programs that contain no side-effects are often simple to reason about because there are no hidden state changes to think about.
Another advantage has to do with data dependencies and incremental processing. Large signal processing operations are often performed incrementally, one sample block at a time. All blocks starting at a particular time are computed before the blocks in the next time increment. The order in which blocks are computed is important because the parameters of a function must be computed before the function is applied. In functional programs, once a parameter (in particular, a block of samples) is computed, no side effects can change the samples, so it is safe to apply the function. Thus, the implementation tends to have more options as to the order of evaluation, and the constraints on execution order are relatively simple to determine.
The functional style seems to be well-suited to many signal-processing tasks. Nested expressions that modify and combine signals provide a clear and parsimonious representation for signal processing.
The functional style has important implications for Nyquist. First, since there are no side-effects that can modify a SOUND, SOUNDs might as well be immutable. Immutable sounds can be reused by many functions with very little effort. Rather than copy the sound, all that is needed is to copy a reference (or pointer) to the sound. This saves computation time that would be required to copy data, and memory space that would be required to store the copy.
As described above, it is possible for the Nyquist implementation to reorder computation to be as efficient as possible. The main optimization here is to compute SOUNDs or parts of SOUNDs only when they are needed. This technique is called lazy evaluation.
In Nyquist, the SOUND data type represents continuous data, and most of the time the programmer can reason about SOUNDs as if they are truly continuous functions of time. A coercion operation allows access to the actual samples by copying the samples from the internal SOUND representation to a Lisp ARRAY type. ARRAYs, of course, are discrete structures by our definitions.
Functions as Instruments and Scores
In Nyquist, Lisp functions serve the roles of both instrument definitions and musical scores. Instruments are described by combining various sound operations; for example, (pwl 0.02 1 0.5 0.3 1.0) creates a piece-wise linear envelope, and (osc c4 1) creates a 1-second tone at pitch C4 using a table-lookup oscillator. These operations, along with the mult operator can be used to create a simple instrument, as in,
;; Define a simple instrument with an envelope.
(defun simple-instr (pitch dur)
(mult (pwl 0.02 1 0.5 0.3 dur)
(osc pitch dur)))
Scores can also be represented by functions using the seq and sim constructs described earlier. For example, the following example will play a short melody over a pedal tone in the bass,
;; Define a simple score function.
(defun simple-score ()
;; bass note
(sim (simple-inst g2 8);; melody simultaneous with bass
(seq (pause 1)
(simple-inst b4 1)
(simple-inst a4 2)
(simple-inst e4 1)
(simple-inst d4 3))))
Nyquist also supports transformation functions for modifying pitch, duration, loudness, and other parameters. The functions are applied using special transformation operators. For example, the following expression would play simple-score transposed up a fifth and accelerated to 0.8 times the normal duration,
(trans 7 (stretch 0.8 (simple-score)))
Transformations may also be continuous functions of time, in which case a SOUND type is used to specify a function. All of the operators available for synthesis can also be used to specify transformation functions.
Behavioral Abstraction
In Nyquist, a behavior is implemented by a function that returns a sound. Supporting the idea that abstract behaviors denote a class of actual behaviors, Nyquist behaviors take parameters. These parameters consist of both conventional function arguments of Lisp, and a set of implicit parameters called the environment. The environment contains transformation attributes that normally affect pitch, loudness, time, articulation, and tempo. The environment is dynamically scoped, meaning that the environment of a "parent" function is passed to each "child" function called. In normal usage, the environment is passed from top-level functions all the way down to the lowest-level built-in functions, which implement the transformations contained in the environment. A function can however override or modify the environment at any time to achieve behaviors that differ from the default.
The expression (osc c4) for example, is a simple behavior that computes a sinusoid lasting one second. The stretch operation normally affects the duration of a behavior, so that,
(stretch 2 (osc c4))
creates a two-second sinusoid. Suppose we wanted to create an "inelastic" behavior that did not stretch? The following will do the job,
(stretch-abs 1 (osc c4))
The stretch-abs operation modifies the environment by replacing the stretch factor by some value (in this case 1). In the following expression, the outer stretch has no effect, because it is overridden by the stretch-abs operation.
(stretch 2 (stretch-abs 1 (osc c4)))
Figure 7 illustrates the information flow in the interpretation of this expression.
insert Figure 7 around here
To give a more concrete example, imagine the problem of a short grace note of fixed length followed by a "stretchable" note. The sequence might be described as follows.
(seq (grace-note) (ordinary-note))
The implementation of grace-note will look something like,
(defun grace-note () (stretch-abs 0.1 (a-note)))
(To keep this definition as simple as possible, we have assumed the existence of a function called a-note, which in reality might consist of an elaborate specification of envelopes and wave forms.) Note how the knowledge of whether to stretch or not is encapsulated in the definition of grace-note. When a stretch is applied to this expression, as in,
(stretch 2 (seq (grace-note) (ordinary-note))
the environment passed to seq and hence to grace-note will have a stretch value of 2, but within grace-note, the environment is modified as in Figure 7 so that a-note gets a stretch value of 0.1, regardless of the outer environment. On the other hand, ordinary-note sees a stretch value of 2 and behaves accordingly.
In these examples, the grace note takes time and adds to the total duration. A stretch or stretch-abs applied to the preceding or succeeding note could compensate for this. Nyquist does not offer a general solution to the ornament problem (which could automatically place the grace note before the beat), or to the transition problem (which could terminate the preceding note early to allow time for the grace note).
In a real program, pitches and other information would probably be passed as ordinary parameters. Here is the previous example, modified with pitch parameters and using the note object with duration, pitch, and amplitude parameters,
;; Define and demonstrate a grace-note function.
(defun grace-note (pitch)
(stretch-abs 0.1 (note 1 pitch 1)))
(stretch 2 (seq (grace-note c4) (note 1 d4 1)))
As these examples illustrate, information flow in Nyquist is top down from transformations to behaviors. The behaviors, implemented as functions, can observe the environment and produce the appropriate result, which may require overriding or modifying the environment seen by lower-level functions. This approach is essentially a one-pass causal operation&endash;parameters and environments flow down to the lowest-level primitives, and signals and stop times flow back up as return values.
The next section will describe the GTF representation language, after which we will discuss implementation issues related to this kind of system in detail.
The GTF Representation Language
GTF (Generalized Time Functions) is a representation language for music. The central aim of its development was is to define constructs that make it easy to express musical knowledge. This would be very useful as the underlying mechanism for a composition system, but at the moment we are only using it for exploring new ideas about music representation. The system uses a mixed representation&endash;some aspects are represented numerically by continuous control functions, and some aspects are represented symbolically by discrete objects. Together, these discrete musical objects and continuous control functions can form alternating layers of information. For example, a phrase can be associated with a continuous amplitude function, while consisting of notes associated with their own envelope function, which are in turn divided into small sections each with its specific amplitude behavior. The lowest layer could even be extended all the way down to the level of discrete sound samples (see Figure 2).
With respect to the continuous aspects (e.g., the vibrato problem), control functions of multiple arguments are used&endash;the so called "time functions of multiple times" or generalized time functions (GTF). These are functions of the actual time, start time and duration (or variations thereof) and they can be linked to any attribute of a musical object to describe the value of that parameter as an envelope evolving over time.
insert Figure 8 around here
If we ignore for the moment the dependence of time functions on absolute start time, they can be plotted as three-dimensional surfaces that show a control value for every point in time given a certain time interval, as in Figure 8. Similar plots could be made to show a surface dependent on start time. A specific surface describes the behavior under a specific time transformation (e.g., stretching the discrete object to which it is linked). In Figure 8, this surface is shown for a simple sinusoidal vibrato and a sinusoidal glissando. A vertical slice through such a surface describes the characteristic behavior for a certain time interval&endash;the specific time function for a musical object of a certain duration (Figure 9).
insert Figure 9 around here
There are also ways of combining basic GTFs into more complex control functions using a set of operators&endash;compose, concatenate, multiply, add, etc.&endash;or by supplying GTFs as arguments to other GTFs. In these combinations the components retain their characteristic behavior.
There are several pre-defined discrete musical objects (such as note and pause) They have standard ways of being combined into compound ones (e.g., using the time structuring functions S and P &emdash;similar to seq and sim in ACF).
All musical objects (like note, s[equential], or p[arallel]) are represented as functions that will be given information about the context in which they appear. The latter supports a pure functional description at this level using an environment for communicating context information (Henderson 1980). Musical objects can be freely transformed by means of function composition, without actually being calculated (see the "lazy evaluation" discussion below). These functions are only given information about their context at execution time, and return a data structure describing the musical object that, in turn, can be used as input to a musical performance or graphical rendering system.
To integrate these continuous and discrete aspects, the system provides facilities that support different kinds of communication between continuous control functions and discrete musical objects. They will be introduced next.
Passing Control Functions to Attributes of Musical Objects
As presented above, there are at least two ways of passing time functions to musical objects. One method is to pass a function directly as an attribute to, for instance, the pitch parameter of a note&endash;specification by parameterization. An alternative method is to make a musical object with simple default values and to obtain the desired result by transformation&endash;specification by transformation. When using the parameterization method, a GTF is passed the start-time and the duration of the note that it is linked to as attribute. For the transformation method, a GTF used in a transformation is passed the start-time and the duration of the compound object it is applied to. Thus, to give it the same power as the transformation method, one needs a construct to "wrap" a control function "around" a whole musical object, and apply it as parameter to the different parts. The example below shows the natural use of the transformation style in applying an amplitude envelope to a compound musical object. It produces output as shown in Figure 10. Note that amplitude, s and p in GTF are similar to loud, seq and sim in ACF, respectively; keyword/value pairs are used to specify a note’s parameters, as in (:duration 2).
;; Apply an amplitude envelope to a phrase of two notes.
(amplitude (ramp 0 1)
(s (note :pitch 60 :duration 2 :amplitude 1)
(note :pitch 61 :duration 1 :amplitude 1)))
The next example shows the alternative specification (see the output in Figure 10). The construct with-attached-gtfs names the amplitude envelope for later reference in parts of a discrete compound musical object and links it (for the time behavior) to the whole object.
;; Attach an amplitude envelope to a phrase.
(with-attached-gtfs ((envelope (ramp 0 1)))
(s (note :pitch 60 :duration 2 :amplitude envelope)
(note :pitch 61 :duration 1 :amplitude envelope))insert Figure 10 around here
Passing Control Functions Between Musical Objects
Once control functions are incorporated into musical objects as attributes, it is interesting to allow later access to them from other musical objects (i.e., the transition problem). The construct with-attribute-gtfs supports this notion, taking care that transformations on attributes of musical objects propagate their effects properly when outside reference to these attributes was made. Control functions are only defined for the duration of the object to which they are linked, but when they can be referred to from musical objects at other time positions, it is useful to be able to evaluate them at other times. This enables extrapolation, for instance, needed in describing what happens in a transition between notes. In Figure 11, a simple example of such a transition transformation is shown. It applies to two notes, derives the pitch control function from both, and calculates an interpolation between them (using the cross-fade GTF operator).
One should note that it is easy to write the example above using a "top-down" communication, defining the control functions in advance, before they are referred to. However, this communication has to be planned, and general encapsulation of musical objects cannot always be maintained. In contrast, allowing access to attributes of musical objects after their instantiation does not discourage abstraction.
;; Define a transition to operate between two notes.
(defun transition (note-a note-b)
(with-attribute-gtfs (((pitch-a :pitch) note-a)
((pitch-b :pitch) note-b))
(s note-a
(note :duration .75 :pitch (cross-fade pitch-a pitch-b))
note-b)))(defun note-1 () (note :pitch (oscillator 62 1 1)))
(defun note-2 () (note :pitch (oscillator 61 3 1)))insert Figure 11 around here
Passing Control Functions Upward
Sometimes a global transformation of an attribute needs to refer to the attribute values of the parts of a complex musical object to which it is applied. This "bottom-up" communication is needed, for instance, when one wants to compress the loudness of musical object (the compressor problem mentioned above). This is an amplitude transformation that needs access to the amplitude of the parts of the object. The total amplitude at any time depends on the sum of the amplitudes of parallel parts, so the amplitude transformation of a specific note relies on its parallel context. Figure 12 shows the type of communication that is needed to write a compressor transformation. The overall amplitude is calculated by summing amplitude contours for parallel sub-structures and concatenating them for sequential ones. This resulting overall amplitude function for the compound musical object can then be compressed&endash;in this simple example by inverting it&endash;and communicated down to each basic musical object by an amplitude transformation.
;; Define an object that can be used with the compress function.
(defun musical-object ()
(p (note :amplitude .1 :pitch 62)
(s (note :duration .75 :amplitude .1 :pitch 61)
(note :amplitude (ramp 0 .8) :pitch 64))
(note :amplitude (ramp 0 .8) :duration .5 :pitch 60)))
;; Define a dynamic range compressor.
(defun compress (musical-object)
(with-attribute-gtfs
(((amp :amplitude #'concatenator #'summer)
musical-object))
(amplitude (gtf-/ 1 amp) musical-object)))insert Figure 12 around here
Implementation Issues
Unfortunately not all work is done when good representations and computational ways of dealing with them are designed. Computer music systems, and especially real-time applications, put a heavy burden on computation resources, and only a wise management of both computation time and memory can help a system that is formally correct to become practically useful too. Luckily, several techniques have emerged for efficient implementation that do not destroy the higher abstract levels of language constructs. These techniques allow the casual user to ignore lower level implementation mechanisms.
Control and Information Flow
A subtle aspect of language design is the nature of control and information flow. This is often critical to the design and implementation of a language and a key to understanding its powers and limitations. We will consider a variety of possibilities.
Top-Down Information Flow
As a first example, consider a typical procedural language such as C or Pascal, with a library of procedures that generate MIDI data. Program evaluation is performed in the usual manner, evaluating inner procedures as they are encountered, using a stack to save the intermediate state of outer (calling) procedures until the inner (called) procedure returns. If all parameters are passed by value (by copying values from the caller to the callee), and if no results are returned from functions, then the information flow is purely top-down. Control flow is depth-first; the structure implied by procedural nesting is traversed in a depth-first order. This means that the next program statement is not evaluated until the current program statement is fully evaluated, including all nested procedures.
Depth-First Information Flow
If functions return values, then the control flow remains depth-first, but the information flow is both top-down and bottom-up. Since information flows to a procedure instance when the procedure is called, and information flows out of the procedure only when it returns, there is essentially a one-pass information flow through the structure as shown in Figure 13.
insert Figure 13 around here Lazy evaluation
While it is natural to organize a program to reflect musical structure, this does not always result in a natural order of execution. For example, if there are two parallel behaviors, a melody and a harmony, a normal depth-first order of evaluation would compute one behavior in its entirety before executing the other behavior. Thus, the "natural" structure of a procedural program does not result in any parallel behavior. In non-real-time programs, this problem can be solved by sorting the output into time order. Alternatively, the procedures that output notes may insert them directly into a sorted note list structure or even into a digital audio sound file as in Cmix (Lansky 1987). The point is that the execution order may not correspond to the time order of the behaviors involved.
The fact that normal execution order and time order are not the same has some important consequences. First, it is not possible to build real-time programs if the execution does not proceed in time order. This limits procedural, normal execution order programs to "out of time" composition tasks. Second, information flow between parallel behaviors can be at best one-way (from the first behavior executed to the second). It is not possible to have two-way or ensemble-like communication because each behavior, for example each voice of an ensemble, is computed in sequence.
One way out of this dilemma is to resort to more elaborate programming models. For example, multiple processes can be used to perform concurrent computation. A good example of a process-based language is Formula (Anderson and Kuivila 1990). Programming with concurrent processes does however require special care if processes share data, communicate, and synchronize.
Alternatively, an "active object" approach can be used to perform interleaved computations. FORMES is an early example of the active object approach (Rodet and Cointe 1984). Active objects are simpler to use than a process-based approach, but still require sophisticated programming techniques.
Perhaps the simplest way to achieve concurrent behavior is with the approach used in "Moxie," a language designed by Douglas Collinge (1985; Collinge and Scheidt 1988) and re-implemented in the CMU MIDI Toolkit (Dannenberg 1986a, 1993a). Here, procedure calls can be deferred to some time point in the future. A periodic process-like behavior results if a procedure performs an action and then calls itself with a delay. These procedural approaches to concurrency deserve a chapter of their own (in fact, many books are written about programming with processes), but we will leave this subject and return to more functional approaches.
An alternative to procedural approaches uses "lazy evaluation," where computation proceeds according to the demand for data. Consider a nested expression: (a • b) + (c • d), where a, b, c and d are signals. In the "normal" order of execution, we would multiply a and b in their entirety. Then we would multiply c and d. Finally, we would add the two products. Note that this order of operation would require space for the intermediate products and the final sum. Since these are signals, the space could be quite large. For example, 16-bit audio at a 44.1KHz sample rate requires 88.2KB of memory per second of audio.
Alternatively, lazy evaluation delays the execution of expressions until the value is needed. This is accomplished by creating a "place-holder" for the expression that can be invoked later to produce the final value. In the case of (a • b), a structure (usually called a suspension) is created to "remember" the state of the operation&endash;that a and b are to be multiplied. Lazy evaluation systems often support the incremental evaluation of expressions. This means that a signal could be computed one sample or one block of samples at a time, leaving the remainder of the computation in suspension.
The Nyquist implementation uses lazy evaluation. In Nyquist, all signals are represented using suspensions that are activated as needed to compute blocks of samples. The expression (a • b) + (c • d), when first evaluated, will create the structure shown in Figure 14. If the beginning of the signal is needed, the "+" suspension requests a block from the first "•" suspension. This suspension in turn requests a block from each of a and b, which may activate other suspensions. The blocks returned from a and b are multiplied and returned to the "+" suspension. Then, the second "•" suspension is called to compute a block in a manner similar to the first one. The two product blocks are added and the sum is returned from the "+" suspension.
insert Figure 14 around here
Lazy evaluation results in a computation order that is not simply one pass over the program structure. Instead, a pass is made over the structure of suspensions each time additional samples are required from the expression. This results in a time-ordered interleaving of a, b, c, and d. A similar technique is used in Music N languages so that samples will be computed in time order with a minimal use of memory for sample computation.
Neither Nyquist nor Music N languages require the programmer to think about data structures, suspensions, or even lazy evaluation. The programmer merely writes the expression, and the implementation automatically transforms it into a lazy structure. This can lead to a very clean notation even though the run-time behavior is quite complex.
Lazy evaluation is a powerful and important technique for music systems because it can automatically convert from an execution order based on musical and program structure to an execution order that corresponds to the forward progress of time. Since the semantics are unchanged by the transformation, however, programming languages based on nested functions (such as Nyquist) still have the limitation that information flow is strictly top-down through parameters and bottom-up via results. To get around this one-pass restriction, more elaborate language semantics are required (the compressor problem).
Constraints, Rules, and Search
Because Nyquist and GTF are rooted in functional programming, most of our examples have considered information flow based on function semantics; information flows from actual to formal parameters and values are returned from a function to the function application site. This is adequate for many interesting problems, and the functional style can lead to elegant notation and simple semantics, but there are also many alternatives. One is procedural or object-oriented programming where data structures are modified as the program executes. Programs can follow links between data objects, resulting in almost arbitrary data flow and data dependencies. One of the main problems with this style, in fact, is the difficulty of maintaining intended relationships and invariant properties among data elements.
To illustrate the problem, consider computing the sum of two signals, A and B. Suppose that MA and MB are memory locations that store the current values of A and B. Computing the sum of A and B at the current time is implemented by computing content(MA) + content(MB). The problem is knowing when the contents of MA and MB are current. If A depends upon several other variables, it may be inefficient to recompute MA every time one of the several variables changes. An alternative is to compute MA from the dependencies only when MA is required, but if there are several points in the program that require a value for MA, it is inefficient to recompute it upon every access. Furthermore, the values on which MA depends may not always be available.
A solution to this dilemma is the use of constraint-based programming (Levitt 1984). In this paradigm, the programmer expresses dependencies as constraints directly in the programming language and the underlying implementation maintains the constraints. For example, if the constraint C = A + B is specified, then any access to C will yield the same value as A + B. The details that achieve this can largely be ignored by the programmer, and the implementor is able to use sophisticated algorithms to maintain constraints efficiently. Since the bookkeeping is tedious, constraint-based systems can automate many programming details that would be necessary in procedural and object-oriented systems.
Another possibility for constraint-based systems is that constraints can be bidirectional. In the previous example, if C and A are given, then a system with bidirectional constraints can compute B = C &emdash; A. This is quite interesting because it means that information flow is determined by the problem instead of the programming language. This would be useful to us in computing durations. Sometimes a sequence must be of a certain duration, in which case the durations of the elements of the sequence are computed from the desired total duration. In other cases, the duration of the sequence is not specified and must be computed as the sum of the durations of the sequence components. This type of flexibility is difficult to achieve in most music programming languages without programming the dependencies and setting the direction of information flow in advance.
Another situation where information flow is extremely flexible is rule-based systems, where a set of rules are applied to a working memory. Rules are usually of the form,
if condition then action
where condition tests the working memory for some property and action performs some modification to the working memory. Rule-based systems are often used for expert systems and ill-structured problems where no straightforward step-by-step algorithm is known. The conventional wisdom is that rules encode units of knowledge about how to solve a problem. By iteratively applying rules, a solution can be found, even though the path to the solution is not known in advance by the programmer. In these situations, the information flow and dependencies between memory objects is very complex.
Both constraint-based systems and rule-based systems can use search techniques to find an evaluation order that solves the problem at hand. The search for a solution can be very costly, though. One of the drawbacks of constraint-based systems and rule-based systems is that they inevitably incur extra overhead relative to a functional program (where execution order is implied by the programming language semantics) or a procedural program (where execution order is given explicitly by the programmer). With constraints and rules, the implementation must compute what to do in addition to doing it. If the problem demands this flexibility, a constraint-based system or rule-based system can perform well, especially if the system has been carefully optimized.
Duration
The duration of a musical object does not always have to be represented explicitly in that object; the time when the object has to end could be specified by a separate stop event. MIDI, a real-time protocol, uses separate note-on and note-off messages to avoid specifying duration before it is known. If this approach is taken, the internal details of the note cannot depend upon the total duration, and some extra mechanisms are needed to decide which start-event has to be paired with a specific stop-event
Even when the duration of an object is handled explicitly, several approaches are possible. In a top-down approach, the duration of a musical object is inherited by the object&endash;an object is instructed to last for a certain duration. In contrast, many musical objects have intrinsic or synthesized durations, including sound files and melodies. In that case the object can only be instructed to start at a specific time, and its duration only becomes available when the object is actually played to its end. A third possibility is to use representations of musical objects that pass durations "bottom up," so that each instance of a compound object computes a duration in terms of its components and returns it.
In Nyquist, durations are intrinsic to sounds. The sound data structure carries a marker indicating the logical stop time for the sound. When a sequence of behaviors is to be computed, the first behavior is instantiated to compute a sound. At the logical stop time of the first sound, the second behavior is instantiated. At the logical stop time of the second sound, the third behavior is instantiated, and so on. An interesting aspect of logical stop times in Nyquist is that high-level events such as the instantiation of a new behavior can depend upon very low-level signal processing behaviors. In contrast, many systems, especially real-time systems, try to separate the high-level control computation from the low-level signal computation. This is so that the high-level control can run at a coarser time granularity, allowing time-critical signal processing operations to proceed asynchronously with respect to control updates. Nyquist does not attempt this separation between control and signal processing. It is convenient to have intrinsic durations determine the start of the next element in a sequence, but this direction of information flow adds noticeable overhead to signal-processing computations.
In GTF, primitive musical objects can be given explicit durations. Compound musical objects constructed directly with the time ordering operations out of these primitive objects then calculate their durations bottom-up. It is possible, though, to write functions that expect a duration argument and construct a compound musical object with an arbitrary time structure&endash;e.g., elongating a fermata instead of slowing down the tempo as a way of making the melody have a longer duration.
Events as Signals
Continuous signals usually carry information from a source to one or more destinations. The output of an instrument may be connected to the input of a mixer for example. In contrast, discrete data does not necessarily have a specific source or destination. In Music N languages, discrete note events are listed in the score language, so there is no specific note source. Each note denotes an instance of an instrument computation, so there is no specific destination either. We could say that the source is the score and the destination is the orchestra, but since there is only one score and one orchestra, this is not very meaningful.
This Music N model, in which events denote an instance of a behavior, is simple but limited. (Nyquist and GTF share this limitation.) Suppose, for example, that we wish to model two MIDI streams, each one connected to a different synthesizer. This is not so simple because each MIDI stream will contain indistinguishable Note-On events, so there is no way to say which stream the Note-On comes from, and there is no destination other than a global behavior named Note-On.
On the other hand, signals do not pose similar problems. If we write a reverberation function called revb in C, then we can apply reverberation to several inputs as follows.
output_1 := revb(input_1);
output_2 := revb(input_2);
output_3 := revb(input_3);
This example contains the germ of an idea. By analogy, we should be able to write
output_1 := synth(input_1);
output_2 := synth(input_2);
But in this case, input_1 and input_2 are MIDI streams, not signals.
Having seen the form of the solution, we need to find language semantics that make this possible! A new data type is required to represent event streams (such as MIDI in this example). The data type consists of a sequence of "events," each consisting of a time, a function name, and a set of actual parameter values. Like signals, event streams may be infinite. We call these "timed streams" to distinguish them from streams in languages like Lucid (Ashcroft and Wadge 1977) where events are accessed by position (first, second, third, ...) rather than time.
It now makes sense to have event stream operators. For example, merge(E1, E2) computes the union of events in streams E1 and E2, and gate(S1, E1) acts as an "event switch" controlled by a Boolean function of time S1. When S1 is true, events pass through, and when S1 is false, events are discarded.
It must also be possible to define new operators involving both signals and event streams. We will not go into great detail here, but imagine something like an object-oriented language class definition. An instance of a user-defined operator on event streams is just an instance of this class, and each event is a message to the instance object. For example, here is C-style pseudo-code for the merge operation that handles only Note-On and Note-Off events.
merge(E1, E2) is [
handle
event E1.NoteOn(c, p, v) is [ send NoteOn(c, p, v) ];
event E1.NoteOff(c, p, v) is [ send NoteOff(c, p, v) ];
event E2.NoteOn(c, p, v) is [ send NoteOn(c, p, v) ];
event E2.NoteOff(c, p, v) is [ send NoteOff(c, p, v) ];
]
Notice the send command, which places a message such as NoteOn(c, p, v) in the output event stream. Also notice that input "messages" come only from event stream parameters. This is markedly different from object-oriented programming systems where messages come from anywhere and message sends always specify a receiver object. Remember also that message streams are values that can be assigned to variables and passed as parameters (such as E1 and E2) to other operations.
The concept of timed streams is not a new one, although the concept has not been studied systematically. Many software systems for MIDI use a stream model for routing MIDI messages among application programs. The NeXT Music Kit (Jaffe 1989) and the programming language Max (Puckette 1991) also allow connections that carry discrete data between software objects. The approach outlined in this section is different in that event streams are immutable values just like signals.
Resource Updates as Signals
The idea of streams is relevant to the resource-instance model. In a pure instance model, every discrete event denotes an instantiation, so it is not necessary to have a specific source or target for the events. In the resource model, the resource (instrument) becomes a destination for a stream of updates, so the idea that discrete events are organized into streams is a natural one.
The event-stream concept is interesting and powerful, especially because many event-transforming operators are possible, including transposition, conditional selection, delay, stretching, and dynamic level changing. Treating events as elements of a stream also clarifies data dependencies (destinations depend upon sources), which in turn relates to the scheduling or ordering of computation.
Conclusion
Languages are a measure of our understanding. Our ability to design good languages for a particular domain (such as music) depends upon our ability to clearly describe the terms, conditions, and concepts of the domain. So far, we have mastered some of the concepts and provided good support for them in a number of music representation languages. Other concepts are not yet well understood, and are not well-supported by languages. The anticipation problem, for example, where current behavior is a function of both the current state and future intensions, is quite interesting. How does one represent and operate upon future plans?
These, and other problems, hopefully make clear that the representation of music still poses a major challenge to language design. We hope that this chapter will lead to a greater understanding of existing languages and will motivate others to find new solutions to the problems we have raised. Perhaps a greater awareness of these issues will also help other language designers to incorporate existing knowledge about language design for music.
Summary
We have surveyed a number of problems in music representation, including the vibrato problem, transitions and anticipation, continuous vs. discrete data, and the link between descriptions of sounds and descriptions of instruments. These problems and the search for their solution influence the design of music representation and programming languages. Some of the language concepts motivated by musical concerns are: behavioral abstraction (or context-sensitive polymorphism); in- and out-of-time processing; various forms of discrete and continuous data; and hierarchical and heterarchical structure. The Nyquist and GTF languages are examples of languages that incorporate many of these concepts while remaining fairly broad in their application. A number of interesting implementation issues arise in music languages, including lazy evaluation, timed event streams, information flow, and duration.
Acknowledgments
This first author would like to thank the School of Computer Science at Carnegie Mellon support in many forms. Part of this work was done during a visit of the last two authors at CCRMA, Stanford University on kind invitation of Chris Chafe and John Chowning, supported by a travel grant of the Netherlands Organization for Scientific Research (NWO). Their research has been made possible by a fellowship of the Royal Netherlands Academy of Arts and Sciences (KNAW).
References
Anderson, D. P., and R. Kuivila. 1990. "A System for Computer Music Performance." ACM Transactions on Computer Systems 8(1): 56-82.
Ashcroft, E. A., and W. W. Wadge. 1977. "Lucid, A Nonprocedural Language with Iteration." Communications of the ACM 20(7): 519-526.
Ashley, R. D. 1992. "Modelling Ensemble Performance: Dynamic Just Intonation." Proceedings of the International Computer Music Conference 1992. San Francisco: International Computer Music Association, pp. 38-41.
Brinkman, A. 1985. "A Data Structure for Computer Analysis of Musical Scores." Proceedings of the 1984 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 233-242.
Cointe, P., and X. Rodet. 1984. "Formes: an Object and Time Oriented System for Music Composition and Synthesis." In 1984 ACM Symposium on LISP and Functional Programming. New York: Association for Computing Machinery, pp. 85-95.
Collinge, D. J. 1985. "MOXIE: A Language for Computer Music Performance." Proceedings of the I984 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 217-220.
Collinge, D. J., and D. J. Scheidt. 1988. "MOXIE for the Atari ST." Proceedings of the 14th International Computer Music Conference. San Francisco: International Computer Music Association, pp. 231-238.
Dannenberg, R. B. 1984. Arctic: "A Functional Language for Real-Time Control." In 1984 ACM Symposium on LISP and Functional Programming. New York: Association for Computing Machinery, pp. 96-103.
Dannenberg, R. B. 1986a. "The CMU MIDI Toolkit." Proceedings of the 1986 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 53-56.
Dannenberg, R. B. 1986b. "A Structure for Representing, Displaying, and Editing Music." Proceedings of the 1986 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 130-160.
Dannenberg, R. B. 1989a. "Real-Time Scheduling and Computer Accompaniment." In M. V. Mathews and J. R. Pierce, eds. 1989. Current Directions in Computer Music Research. Cambridge, Massachusetts: MIT Press, pp. 225-262.
Dannenberg, R. B. 1989b. "The Canon Score Language." Computer Music Journal 13(1): 47-56.
Dannenberg, R. B. 1992a. "Time Functions," letter. Computer Music Journal, 16(3), 7-8.
Dannenberg, R. B. 1992b. "Real-Time Software Synthesis on Superscalar Architectures." In Proceedings of the 1992 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 174-177.
Dannenberg, R. B. 1993a. The CMU MIDI Toolkit. Software distribution. Pittsburgh, Pennsylvania: Carnegie Mellon University.
Dannenberg, R. B. 1993b. "The Implementation of Nyquist, A Sound Synthesis Language." Proceedings of the 1993 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 168-171.
Dannenberg, R. B., and C. L. Fraley. 1989. "Fugue: Composition and Sound Synthesis With Lazy Evaluation and Behavioral Abstraction." Proceedings of the 1989 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 76-79.
Dannenberg, R. B., C. L. Fraley, and P. Velikonja. 1991. "Fugue: A Functional Language for Sound Synthesis." IEEE Computer 24(7): 36-42.
Dannenberg, R. B., C. L. Fraley, and P. Velikonja. 1992. "A Functional Language for Sound Synthesis with Behavioral Abstraction and Lazy Evaluation." In Denis Baggi, ed. 1992. Readings in Computer-Generated Music. Los Alamitos, California: IEEE Computer Society Press, pp. 25-40.
Dannenberg, R. B., P. McAvinney, and D. Rubine. 1986. "Arctic: A Functional Language for Real-Time Systems." Computer Music Journal 10(4): 67-78.
Dannenberg, R. B., D. Rubine, and T. Neuendorffer. 1991. "The Resource-Instance Model of Music Representation." Proceedings of the 1991 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 428-432.
Desain, P., and Honing, H. 1991. "Towards a Calculus for Expressive Timing in Music." Computers in Music Research, 3, 43-120.
Desain, P., and H. Honing. 1988. "LOCO: A Composition Microworld in Logo." Computer Music Journal 12(3).
Desain, P., and H. Honing. 1992a. "Time Functions Function Best as Functions of Multiple Times." Computer Music Journal, 16(2). Reprinted in Desain and Honing 1992b.
Desain, P., and H. Honing. 1992b. Music, Mind and Machine, Studies in Computer Music, Music Cognition and Artificial Intelligence. Amsterdam: Thesis Publishers.
Desain, P., and H. Honing. 1993. "On Continuous Musical Control of Discrete Musical Objects." Proceedings of the 1993 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 218-221.
Henderson, P. 1980. Functional Programming. Application and Implementation. London: Prentice-Hall.
Honing, H. 1990. "POCO: an Environment For Analysing, Modifying, and Generating Expression in Music." Proceedings of the 1990 International Computer Music Conference. San Francisco: Computer Music Association, pp. 364-368.
Honing, H. 1992. "Expresso, a Strong and Small Editor for Expression." Proceedings of the 1992 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 215-218.
Honing, H. 1993. "Issues in the Representation of Time and Structure in Music." In I. Cross and I. Deliège, eds. 1993. "Music and the Cognitive Sciences." Contemporary Music Review. 9, 221-239. Preprinted in Desain and Honing 1992b.
Honing, H. 1995. "The Vibrato Problem, Comparing Two Solutions." Computer Music Journal, 19(3): 32-49.
Jaffe, D., and L. Boynton. 1989. "An Overview of the Sound and Music Kit for the NeXT Computer." Computer Music Journal 13(2): 48-55. Reprinted in S. T. Pope, ed. 1991.The Well-Tempered Object: Musical Applications of Object-Oriented Software Technology. Cambridge, Massachusetts: MIT Press.
Lansky, Paul. 1987. CMIX. Software distribution. Princeton, New Jersey: Princeton University.
Levitt, D. 1984. "Machine Tongues X: Constraint Languages." Computer Music Journal 8(1): 9-21.
Loyall, A. B, and J. Bates. 1993. "Real-time Control of Animated Broad Agents." Proceedings of the Fifteenth Annual Conference of the Cognitive Science Society, Boulder, Colorado: Cognitive Science Society.
Mathews, M. V. 1969. The Technology of Computer Music. Cambridge, Massachusetts: MIT Press.
Mathews, M. V. and F. R. Moore. 1970. "A Program to Compose, Store, and Edit Functions of Time." Communications of the ACM 13(12): 715-721.
Moore, F. R. 1990. Elements of Computer Music. New York: Prentice-Hall.
Morrison, J. D. and J. M. Adrien. 1993. "MOSAIC: A Framework for Modal Synthesis." Computer Music Journal 17(1): 45-56.
Puckette, M. 1991 "Combining Event and Signal Processing in the Max Graphical Programming Environment." Computer Music Journal 15(3): 68-77.
Rodet, X., and P. Cointe. 1984. "FORMES: Composition and Scheduling of Processes." Computer Music Journal 8(3): 32-50. Reprinted in S. T. Pope, ed. 1991.The Well-Tempered Object: Musical Applications of Object-Oriented Software Technology. Cambridge, Massachusetts: MIT Press.
Smith, J. O. 1992. "Physical Modeling Using Digital Waveguides." Computer Music Journal 16(4): 74-91.
Vercoe, B. 1985. "The Synthetic Performer in the Context of Live Performance." Proceedings of the 1984 International Computer Music Conference. San Francisco: International Computer Music Association, pp. 199-200.
Vercoe, B. 1986. Csound: A Manual for the Audio Processing System and Supporting Programs . Cambridge, Massachusetts: MIT Media Lab.
Xenakis, I. 1971. Formalized Music. Bloomington, Indiana: Indiana University Press.
Figure Captions
Figure 1. The vibrato problem&endash;what should happen to the form of the contour of a continuous control function when used for a discrete musical object with a different length? For example, a sine wave control function is associated with the pitch attribute of a note in (a). In (b) possible pitch contours for the stretched note, depending on the interpretation of the original contour, are shown. Second, what should happen to the form of the pitch contour when used for a discrete musical object at a different point in time (c)? In (d) possible pitch contours for the shifted note are shown. There is, in principle, an infinite number of solutions depending on the type of musical knowledge embodied by the control function.
Figure 2. The specification of a musical object is shown here in the form of alternating layers of continuous and discrete representation, each with its own time-stretching and shifting behavior.
Figure 3. Examples of basic and compound musical objects in ACF and GTF are given in Lisp and graphical pitch-time notation&endash;a note with pitch 60 (as a MIDI key number, = middle C), duration 1 (second or beat), and maximum amplitude (a), a sequence of a note, a rest and another, shorter note (b), and three notes in parallel, each with different pitches and amplitudes (c).
Figure 4. A sequence of a user-defined musical object (a melody) repeated twice.
Figure 5. Two examples of notes with continuous pitch attribute are illustrated here. A interpolating linear ramp with start and end value as parameters is shown in (a), and a sine wave oscillator with offset, modulation frequency and amplitude as parameters is given in (b).
Figure 6. This figure shows several examples of transformations on musical objects: a stretch transformation (a), an amplitude transformation (b), a pitch transformation (c), a nesting of two transformations (d), a time-varying pitch transformation (e), and a time-varying amplitude transformation (f).
Figure 7. Information flow showing how Nyquist environments support behavioral abstraction. Only the stretch factor is shown. The outer stretch transformation alters the environment seen by the inner stretch-abs transformation. The stretch-abs overrides the outer environment and passes the modified environment on to the osc function. The actual duration is returned as a property of the sound computed by osc.
Figure 8. Two surfaces showing functions of elapsed time and note duration for different stretch behaviors are shown here. In the case of a sinusoidal vibrato, one needs to add more periods for longer durations (a), but a sinusoidal glissando stretches along with the duration parameter (b).
Figure 9. This shows a more complex function of time and duration. The appropriate control function to be used for an object of a certain duration is a vertical slice out of the surface.
Figure 10. Continuous attributes of compound musical objects can be obtained either by transformation or parameterization (see text for the program code).
Figure 11. A sequence of two notes with continuous time functions associated with their pitch attributes can be seen in (a), and the result of applying a transition transformation in (b).
Figure 12. Two notes in parallel with different amplitude envelopes are shown in (a), and the result of applying a compressor transformation to this in (b).
Figure 13. When nested procedures or functions are evaluated in the usual depth-first order, information is passed "down" through parameters and "up" through returned values. The information flow over the course of evaluation is diagrammed here. Note that in conventional stack-based language implementations, only portions of this tree would be present at any one instant of the computation.
Figure 14. The expression (a • b) + (c • d), when evaluated lazily, returns a suspension structure as shown here rather than actually performing the computation.
Figures

Figure 1.
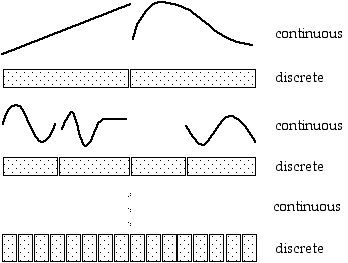
Figure 2.
(note 60 1 1) Þ
(seq (note 62 1 1)
(pause 1)
(note 61 .5 1)) Þ
(sim (note 62 1 .2)
(note 61 1 .8)
(note 60 1 .4)) Þ
Figure 3.
(seq (melody) (melody)) Þ
Figure 4.
(note (ramp 60 61) 1 1) Þ
 (a)
(a)
(note (oscillator 61 1 1) 1 1) Þ
 (b)
(b)
Figure 5.
(stretch 2 (melody)) Þ
 (a)
(a)
(loud -0.4 (melody)) Þ
 (b)
(b)
(trans 2 (melody)) Þ
 (c)
(c)
(trans 2 (loud -0.4 (melody))) Þ
 (d)
(d)
(trans (ramp 0 2) (note 60 1 1)) Þ
 (e)
(e)
(loud (ramp 0 -1) (note 62 1 1)) Þ
 (f)
(f)
Figure 6.
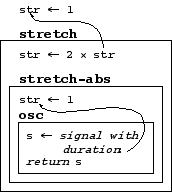
Figure 7.
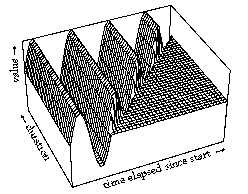 (a)
(a)
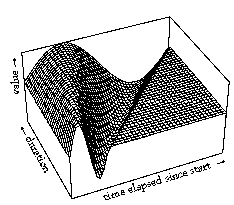 (b)
(b)
Figure 8.
Figure 9.
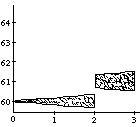
Figure 10.
(s (note-1) (pause :duration .75) (note-2)) Þ
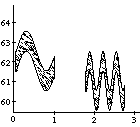 (a)
(a)
(transition (note-1) (note-2)) Þ
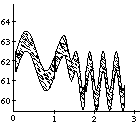 (b)
(b)
Figure 11.
(musical-object) Þ
 (a)
(a)
(compress (musical-object)) Þ
 (b)
(b)
Figure 12.
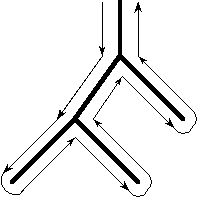
Figure 13.
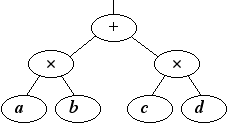
Figure 14.