We found all kinds of references in the literature and read a lot that evening. It was amazing to find how much work actually was done on a problem that we had thought was not a problem at all. We became a little bit more conscious of the whole thing. It looked as if P's hobby horse, psychology, had to be given a chance. He explained that the perception of time had been modelled postulating a certain (often exponential) relation between objective time and experienced time. But this research had all been done with impoverished stimulus material, often consisting of just one time interval marked-off with two clicks. `Other research,' P added, `found that duration judgment depends on the way the interval is filled with more or fewer events, so unfortunately these simple laws cannot be directly applied to more complex material like real music.' Even P was disappointed with the results of his beautiful science. `But psychology has something to offer to us here', he spoke in a defensive tone. `Take a look at all the articles that present timing or tempo measurements in the form of continuous curves instead of just a scattergram of measurements. These curves more or less imply an independent existence, apart from the rhythmic material where they were measured from. But psychological research has shown that one cannot perceive timing without events carrying it.' He found this convincingly argued in an article by the psychologist James J. Gibson called "Events are perceivable but time is not". `Can you imagine perceiving a rubato without any notes carrying it?' P asked. `And vise versa: "filling up" time by adding an event between two measured points is problematic, isn't it?' There seemed to be no possible argument.
Glossary on Subjective Time, Duration and Tempo Magnitudes.
We decided to do the acid test using a feature of the sequencer program. In this program it was possible to copy tempo tracks from one piece to the other. We applied the tempo track of the original performance of the theme (see Figure 2) to the score of the first variation. [play] The result was poor; even we could hear that. The timing made sudden jumps, like a beginner sight-reading and hesitating at unexpected points because of a difficult note. The expressive timing pattern found in the theme did not "fit" the variation. Our friend's performance of the variation was much smoother and had gestures on a larger scale, as far as we were able to judge (Figure 4). Also, the other way around, taking the timing data from the variation and applying it to the score of the theme had the same awkward effect. [play] It seemed impossible to just add or remove notes using these stepwise tempo curves. We felt stupid again for having assumed that the independence of tempo tracks in the sequencer made musical sense. But it made us look in the literature for alternatives.

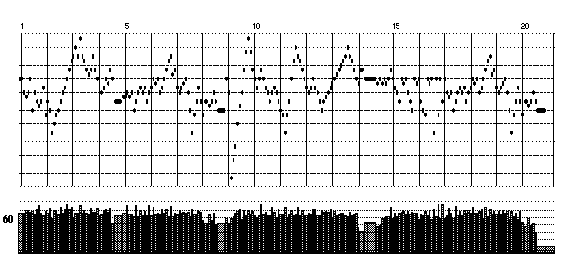
Figure 4. Tempo deviations in the performance of the variation at tempo 60.
The answer was not far away. In the field of computer music research continuous rubato curves were used almost by default. We decided to take the path of the continuous timing functions, hoping it would get rid of this awkward "jumpiness". Thus M's hobby horse was brought out again. `Functions are far easier to handle. One can calculate, given the right kind of function, a good timing curve for every piece,' M argued convincingly. This combined approach of formality (in the mathematical sense) and pragmatics reminded us of a method developed by David Jaffe of CCRMA to model the timing of different parts of a computer orchestra. Jaffe wanted the different instruments to have their own timing, but they had to synchronise at specific points as well. By using a time map, instead of tempo changes, coordination and synchronization became possible. `What he actually does is to specify the timing for each event by means of a function from score time to performance time,' M explained, `a blatantly simple idea indeed: to integrate velocity or one-over-tempo, as Jaffe calls it, to get time. This of course restrains the possible functions one can use to make up such a time map; they have to increase monotonously and one must be able to calculate a first derivative.' This was again a method, among many others, in which different authors presented their ideas of tempo curves (see Figure 5). We tried to bring some order to the ways the different representations were used.
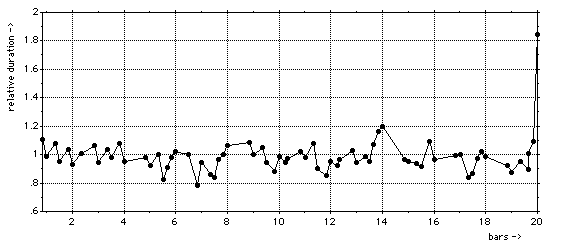
Figure 5. A typical so called "Tempo Curve", with duration factors for each note as a function of metrical time.
Soon M gave up, stating that it was a hopeless mess; no two authors used the same dependent and independent variables and measurement scales. And while in the end all the information needed could be extracted from most presentations, it was a difficult job, the more so because of the confusion in terminology. We decided to return to the practical application of the time map. We adapted the sequencer's tempo track to contain a time map (composed of line segments) instead of the discrete tempo changes we had used before. We then applied this continuous curve to the variation and had our pianist judge it. [play] He thought it was much better than the direct application of the discrete curve of the theme to the variation. The interpolation (with line segments) did improve the smoothness of the timing, but he still complained about the sudden tempo jumps at the junctions of the curve. M remarked that one could restrict the allowed tempo map functions further or smooth the existing function, for instance, with splines. This brought us to an article describing work done at IRCAM by David Wessel and others, which indeed proposes the use of splines. We took an algorithm we had lying around that did splines and added it to our tempo track algorithm. And there it was: with some twiddling of the parameters we could interpolate the timing pattern of the theme for its use on the variation. We almost thought that with this interpolation we had proven Gibson wrong. There was a smooth sense of timing in between events, and if one is smart enough one can tap it and hook new events onto it in a reasonable way. But our musical friend did not agree `Reasonable?' he reacted angry, `it sounds reasonable, yes, but your numerical calculations have nothing to do with the way I played it, whatsoever. The musical structure, my dear friends, remember the musical structure. How often do I have to repeat this. Timing is related to structure!' We suggested to him a cup of tea, in the hope that this would calm him down.