[Published as: Desain, P., & Honing, H. (1994). Rule-based models of initial beat induction and an analysis of their behavior. In Proceedings of the 1994 International Computer Music Conference. 80-82. San Francisco: International Computer Music Association.]
In this paper a family of rule-based beat induction models is described (Longuet-Higgins & Lee, 1982; Lee, 1985; Longuet-Higgins, 1994), and introduces a new analysis method that goes beyond evaluating the models on a small set of carefully chosen musical examples.
Longuet-Higgins & Lee (1982) propose a rule-based model of beat induction that was unique, at the time, because of its incremental nature and its focus on the initial stages of beat induction. In this respect the theory is complementary to models that assume an initial beat has already been established (Longuet-Higgins, 1976), or deal with infinite (cyclic) patterns (Povel & Essens 1985; Parncutt, 1994).
In this paper we will compare the Longuet-Higgins & Lee (1982) model to two recent refinements of the original, i.e., Lee (1985) and Longuet-Higgins (1994). They will be referred to as LHL82, L85, and LH94. Related rule-based models are described in Lee (1991) and Scarborough, Miller & Jones (1992), but we will not discuss them here.
LHL82 describes a beat induction theory with a collection of musical examples and computation traces, along with a clear description of the rule-set that made up the original program. Some rules where not described in a formal way, and interactions between the rules were not made explicit, and had to be rationally reconstructed. The original program that was used to generate the output was not available anymore.
L85 describes a "paper and pencil" model of beat induction -it was never implemented. Several unformalized aspects, as well as interactions between the rules unforeseen by the author (Lee, personal communication) had to be filled-in, to be able to produce an implementation that could replicate the examples given in L85. Furthermore, this model has the awkward characteristic -from a perceptual standpoint-, that the UPDATE rule sometimes has to wait forever until it can execute its action.
L94 is a refinement of LHL82, in the sense that some rules were combined and unformalized parts were made explicit. A small computer program in POP-11, describing the model, was made available by its author. The (modified) theory behind the program is not yet published.
Note that in these programs some rules have the same name (e.g., UPDATE) but a completely different definition.
All three models take note duration values as input (expressed as integral multiples of a 16th-note) rather than, for example, attempting to identify the note onsets in an expressive real-time performance. They initially assume the beat to be equal to the time interval between the first two onsets, and then works their way through the incoming material, shifting, doubling and stretching the beat. All three theories make use of the notion of time-pointers (named t1, t2 and t3). They are moved by the rules -after initially pointing to the first and second onset-, to different positions in the pattern. t3 is defined as t2+(t2-t1), and is the predicted next beat.

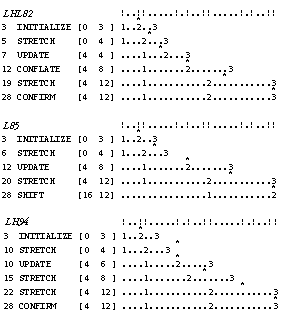
Figure 1. Computation traces for the three rule-based models. See text for details.
In both LHL82 and L85 traces were shown that aligned the specific rule that fired and the new proposed beat with the common music notation. Some rules, though, look further ahead in time than others. In our implementation of these models we inserted a temporal pointer into the computation traces that indicates how much material was available when the beat was updated. With this extension, the models can be interpreted as an algorithm for foot-tapping in real-time (i.e., controlling a mechanical shoe), and it is possible to calculate precisely how far ahead in time the output of a tap can be planned.
As a concrete example, consider the musical fragment in Figure 1. The traces are read left to right and top to bottom. The top line gives the input pattern in grid notation (with "!" for onset and "." for silence) and its equivalent in common music notation. A line describes, first, the time a rule fires (first column); this time position is indicated with a * in the preceding line aligned with the input pattern. Second, the resulting updated beat (second column) of the form [<start-time or "phase"> <beat-duration>]. Finally, the new position of the time-pointers with respect to the input pattern (shown as numbers aligned with the input pattern). For this specific fragment, all three models produce the same beat, but by a different combination and order of application of the rules. Space limitations keep us from discussing the definition of these rules and their differences here.
There are several difficulties that arise when interpreting these rule-based theories as models for foot-tapping. A first question that arises is, when is a beat a proper beat, and when just an intermediate state of computation? L94 makes this explicit and makes a distinction between un-confirmed beats (i.e., an ongoing, yet incomplete state) and confirmed beats (see Figure 1c, last line). After a beat is confirmed the processing stops. For LHL82 such a rule can simply be added, based on the observation that in certain states no other rule could ever fire anymore (i.e., the model becomes "deaf") and an implicit confirmation takes place (see Figure 1a, last line). L85 is special in the sense that it keeps processing its input; we interpreted the moments of moving the pointers to the next beat (i.e., without changing its phase and duration) as a temporary confirmation (see Figure 1b, last line).
These confirmed beats where taken as the output of the respective models, and were used in the analyses described below.
In contrast to the example used in Figure 1, many temporal patterns are treated differently by the three models and yield a different beat. It is hard to get firm conclusions about the behavior of the models by studying the detailed workings of the rules on a small set of musical examples since the interaction between the rules is too complex to reason about. We chose to study the global behavior of the models in a rough statistical way, by characterizing the behavior of each model as the partitioning of the set of all possible inputs into classes of patterns that yield the same result and comparing these partitions. We searched good graphical representations of these analyses, examples of which will be presented here.
The universes of temporal patterns that we used are a collection of nested, abstract sets that are combinatorially complete (we only mention two of them here), and one large corpus of composed rhythms. The first test-set is the universe of all grid-based temporal patterns of a certain duration. This set is almost completely free of assumptions about musical knowledge and structure and will encompass, next to rhythms that can be easily remembered and performed musically, many examples that will be hard to interpret rhythmically at all. Removing all patterns from the previous set that cannot be generated from a simple metrical grammar (using only binary and tertiary subdivisions) gives us the subset of strictly metrical sequences. These patterns have a simple metrical interpretation in which each durational interval fits one level of a metrical hierarchy directly. The patterns are strictly metrical in the sense that there is no syncopation nor tied notes. Furthermore, all patterns start at the begin of a bar -there are no pickups. These patterns form a set of highly structured, simple musical rhythms. Note that they can still be ambiguous -some patterns can be generated from different meters. Finally, to stay in line with the beat induction literature that shows a preference for musical ditty's, we decided to include a set of composed material: a corpus of national anthems (Shaw & Coleman, 1960). And although nationalism is contrary to world-wide collaboration in beat-finding research -the pieces were composed to strongly induce a frame of mind, if not a beat, and as such the set has its merits.
Theoretically the full test sets could be fed into the models and the exact size of each class of same-beat patterns calculated. However, the enormous size of the sets prohibits this (e.g., the size of the set of all grid-based temporal patterns of duration n is in the order 2n). We used a practical way to yield reasonable estimates by Monte Carlo simulation: sampling the sets in a fair way and counting the response categories that arose (the estimates used here are within a 5% error margin). This makes us fully equipped to undertake a global statistical characterization of the behavior of the models. We will first tackle the questions about the consequences of the slightly different rules in the three models.
The first simulation sampled patterns from the sets and categorized the answers of the models into four classes: the class of patterns for which the three models agreed on the same beat, the class of patterns that resulted in three different answers, and the three classes of patterns for which two models agreed. We allowed a multiplication of the beat duration by a power of 2 to still count as an identical beat.
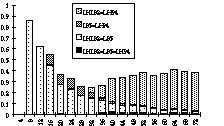
Figure 2. The agreement between the models for the set of all patterns (proportion vs. pattern duration).
Figure 2 shows the fraction of all grid-based patterns that yield a confirmed compatible beat (as defined above) in different models versus the pattern duration. The full height of a bar represents the fraction of patterns for which as least two models agree. The black part of each bar shows the proportion of patterns that are assigned the same beat in all three models. For example, it can be seen that the fraction of patterns, on which the three models agree unanimously, is almost zero. The agreement between LHL82 and L85 is very high for short patterns but decreases toward zero for long ones, whereas the agreement between LHL82 and LH94 increases (towards .4) for longer patterns. Some more conclusions from these analyses for the other universes of patterns are given later.
The next simulation probed the speed of the beat induction in the three rule-based models. Figure 3 shows it in the form of the fraction of confirmed beats versus the pattern duration, for the set of all grid-based patterns. It can be seen that for longer patterns, LHL82 confirms all, L85 70% and L94 about 40% of all patterns, with L85 confirming relatively fast and LH94 confirming relatively slow.
Because it is quite natural to need more time to establish a beat of a longer time interval, a different, and possibly fairer representation of the same data is made by expressing the time needed for confirmation relative to the duration of the beat found. In general, most patterns need about twice the beat length to confirm a beat.

Figure 3. Speed of beat induction for the set of all patterns (proportion vs. pattern duration).
Given that a model came up with a confirmed beat, one might wonder in what range the beat durations and phases are, and whether there are any preferences regarding these. In Figure 4 this distribution -the beat space- for L85 is given for the set of all long patterns (of duration 70). Each bar represents the fraction of patterns that was assigned a certain beat duration, it is subdivided in regions for each phase. It is surprising that the distribution of durations is almost continuous, considered the symbolic, discrete notion of the system. Furthermore, it can be seen that the model has no preference for a specific phase. Other conclusions that can be made from this kind of analysis are given later.
For some of the subsets the question about the correctness of the results of the models can be answered. For the set of strictly metrical patterns, correct beats can be defined to be those that fit one of the metrical levels of one of the generating meters. For the set of national anthems, a correct beat can be defined as a beat that is compatible with the meter notated in the score. The results of these analyses are gathered in the next paragraph.
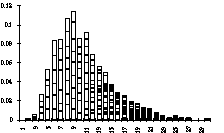
Figure 4. Beat space for L85 (proportion vs. beat duration).
From the analysis of agreement of the three models on the different sets of patterns the following observations can be made. While the set of all rhythms resulted in almost no unanimous agreement, the set of strictly metric patterns gave rise to about 10% and the set of anthems to 20% identical answers. This may reflect the increased amount of musical structure in the latter two pattern sets.
From the analysis of the confirmation speed, the conclusion can be drawn that for the set of strictly metrical patterns the proportion of confirmations increases, compared to the set of all patterns. For the anthems set similar behavior can be observed. In general, for all three models most patterns need twice the beat lengths to confirm a beat, which is amazingly fast compared to, e.g., statistical models.
The beat spaces of the different models are quite different. For LHL82 beat durations longer or equal than 16 are preferred and for both LHL82 and LH94 there is a clear preference for beats with zero phase, i.e., an interpretation without upbeats.
The preliminary results of the correctness analysis for the set of strictly metrical patterns (of duration 70) are 40% for LHL82, 30% for L85, and 50% for LH94. For the national anthems, 59% are correct for LHL82, 37% correct for L85, and 68% correct for L94.
We hope to have showed that these methods are a promising way of characterizing the behaviour of computational models of beat induction in general terms. Our plans are to extend this method to families of models that are based on alternative formalisms.
Special thanks to Christopher Longuet-Higgins for his contribution in several discussions, and providing access to his programs. Part of this work was done while visiting CCRMA, Stanford University on kind invitation of Chris Chafe and John Chowning, supported by a travel grant of the Netherlands Organization for Scientific Research (NWO). The research of the authors has been made possible by a fellowship of the Royal Netherlands Academy of Arts and Sciences (KNAW).