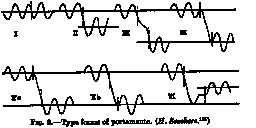
Figure 1. Types of Portamento used in singing (from Seashore, 1967, p. 272).
Peter Desain (NICI) & Henkjan Honing (ILLC)
[Published as: Desain, P., & Honing, H. (1995). Towards algorithmic descriptions for continuous modulations of musical parameters. In Proceedings of the 1995 International Computer Music Conference. 393-395. San Francisco: ICMA. ]
Abstract: A workbench is presented to help in modeling the regularities found in continuous parameter changes of music performance. In modeling these continuous aspects algorithmically, we hope to get a better understanding of their anatomy. The initial focus is on pitch changes: vibrato and portamento, and on the regularities that can be found in their performance.
Most of the research in the psychology of music dealing with expression is concerned with the discrete aspects of music performance, and mainly concentrates on the study of piano music. In these studies only the time of attack of individual notes (and possibly the release time) is studied as carrier of musical expression. However, in wind instruments and most notable in voice, that what happens during and in between the notes is sometimes more relevant then the realization of the note onsets themselves (Strawn, 1989), but this issue is not often addressed in music psychology. A noteworthy exception is the work of Seashore (1967) who pointed at the musical and perceptual importance of the continuous aspects in music performance. He and his colleagues studied, for instance, the use of vibrato in violin playing and of portamento in singing. The musical parameters were analyzed through so-called "performance scores" in which, next to the conventional music notation, pitch and dynamic contours where notated (extracted from sonograms). Musicians achieve a high level of control and systematic consistency over the fine details of pitch and amplitude contours in their performances. Large perceptual differences in how, e.g., a particular vibrato ends at a certain phase and glides from one note to another, indicate that this type of control is essential in music performance. See, for example, Figure 1, showing hand-drawn idealizations of the use of portamento in singing, derived from sonograms.

Figure 1. Types of Portamento used in singing (from Seashore, 1967, p. 272).
It is remarkable that, since these early exploratory studies, this field received little attention (exceptions are, e.g., Chafe, 1989; Clynes, 1987), even though this type of analysis can be made far more easily with current techniques. A reason for this could be the relative inaccessibility for psychologists and musicologists of the data processing techniques needed. However, from the domain of signal processing and computer music several synthesis and analysis methods are available at present. Recent techniques combine Short Time Fourier transforms with "intelligent" peak-tracking (Quatieri & McAulay, 1985; Serra, 1989) and form a solid basis for the analysis and synthesis of these modulation signals. Another reason for the neglect of this field is the amount of information present in these modulation signals. Compared to discrete data there are many more degrees of freedom to explain. And finally, direct experimentation without a model rarely gives results that go beyond the exploratory studies of Seashore and his colleagues.
However, while the availability of current signal processing techniques makes the modulation signals (of pitch or dynamics) easier to extract, their shape is still quite complex. It is difficult to analyze and model them directly. We propose to first decompose these measured modulation signals into idealized components, whose behavior under different temporal conditions can then be studied separately.
As a concrete example, consider measured transitions between two notes with a vibrato, like those depicted in Figure 1. From visually inspecting these curves, the hypothesis may arise that such a transition (Figure 2a) can be decomposed into an additive combination of a periodic signal (the vibrato for each note; see Figure 2b) with a certain development over time (frequency and depth), and a monotonic transition function (e.g., a sigmoid; see Figure 2c) which describes the path from the pitch from the first to the second note. In turn, the vibrato (Figure 2b) can be modeled as a sine wave, parametrized with a decreasing linear ramp for its frequency (Figure 2d) and a decreasing amplitude (Figure 2e).
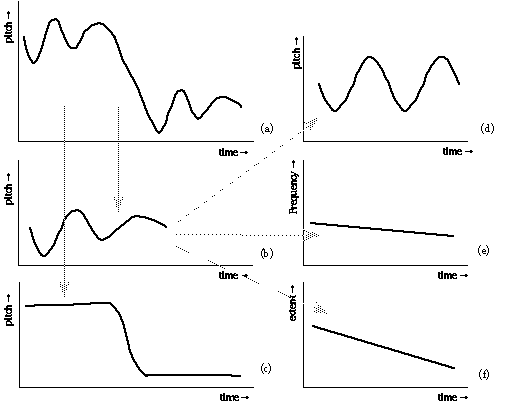
Figure 2. Decomposition of a transition between two notes.
This proposed decomposition can be formalized and verified using a workbench, named Trico, that is designed for the construction of control functions for sound synthesis. It facilitates the composition of abstract control functions based on a formalism named GTF (Desain & Honing, 1992, 1993; Honing, 1995). The user can build the mathematical model of the proposed decomposition helped by the availability of a library of basic functions and standard ways of combining them and by a graphical and aural user-interface for evaluating the first results. The Trico system provides tools to estimate the best parameter settings for the function, optimizing the fit between synthesized and measured data, using methods like simulated annealing (Otten & van Ginneken, 1989) that can be used to minimize the error of the residual. In this way a reasonable algorithmic description of individual note transitions can be obtained. For example, the transitions I to V in Figure 1 can be described by the one compound GTF control function with six parameters (using the decomposition shown in Figure 2).
To move from an idiosyncratic formal model of one specific transition, Trico supports model fitting to multiple instances at once, be they repeated performances of the same transition, repeated occurrences of the same musical material, or even transitions in which, for example, the duration of the notes differ. The basic functions in GTF have access to multiple notions of time (start-time, duration and absolute time), which makes it possible to express abstract temporal behavior non-procedurally. With temporal behavior we mean here how a function changes when it is applied to, for instance, a longer or a later time interval. For example, a vibrato adds more cycles when applied to a longer duration, while a glissando stretches elastically when allowed to take more time. Thus one abstract function might be constructed that models the behavior of a larger class of transitions. This allows the definition of a much more general description of the phenomenon and brings out the regularities observed by all instances.
Of course, the generality of the thus constructed descriptions depends on the availability of data from different conditions. For example, when the ending of a vibrato can be studied for notes of different durations, and in different contexts of subsequent material, a constraint on the end of the vibrato function may be found (e.g., always complete a vibrato cycle before moving to the next note) and when studying transitions over different pitch intervals a regularity observed by Clynes (1987) may be found (i.e., the point of deepest vibrato is dependent on the direction of the subsequent pitch-leap). These regularities can be much easier assessed in such a model-driven approach.
The aim of this study is to proceed beyond the identification of perceptual differences and informal discussions of continuous aspects in music performance. In modeling the these computationally we hope to gain a better understanding of their anatomy. When a good model for a specific instrument and playing style is achieved, it forms a computational description of the rules and structural regularities contributing to our understanding of music performances. Moreover, it can be used to drive sound synthesis models for generating computer music pieces (e.g., Serra, 1989; Smith, 1992), in which these continuous aspects have been brought under direct, but high-level, control of the composer.
Chafe, C. (1989) Simulating performance on a bowed instrument. In M. Mathews & J. Pierce (eds.) Current Directions in Computer Music Research. Cambridge, MIT Press. 185-198.
Clynes, M. (1987) What can a musician learn about music performance from newly discovered microstructure principles (PM and PAS)? In A. Gabrielson (ed.) Action and Perception in Rhythm and Music, Royal Swedish Academy of Music, No. 55.
Desain, P., & Honing, H. (1992). Time functions function best as functions of multiple times. Computer Music Journal, 16(2), 17-34.
Desain, P., & Honing, H. (1993). On Continuous Musical Control of Discrete Musical Objects. In Proceedings of the 1993 International Computer Music Conference. San Francisco: International Computer Music Association.
Honing, H. (1995). The vibrato problem, comparing two solutions. Computer Music Journal, 19(3)
Otten, R.H.J.M. & L.P.P.P van Ginneken (1989) The Annealing Algorithm. Boston: Kluwer
Quatieri, T.F. and R. J. McAulay (1985). Speech Analysis/Synthesis Based on a Sinusoidal Representation. Technical Report 693. Cambridge: MIT.
Seashore, C. E. (1967) Psychology of Music. New York: Dover. (Originally published in 1938).
Serra, X. (1989). A system for sound analysis/transformation/synthesis based on a deterministic plus stochastic decomposition. Department of Music Report No. STAN-M-58, Ph.D. dissertation, Center for Computer Music Research in Music and Acoustics, Stanford University.
Smith, J. O. (1992). Physical Modeling Using Digital Waveguides. Computer Music Journal, 16(4)
Strawn, J. (1989) Approximations and Syntactic Analysis of Amplitude and Frequency Functions for Digital Sound Synthesis. In C. Roads (ed.) The Music Machine. 671-692