The central purpose of the investigation is both to elaborate further the methodology for computational modeling and to show how this method can be instrumental in the understanding of the structure of musical knowledge and the processes involved in music cognition.
The study builds upon three disciplines: musicology, psychology and computer science. By starting from the margins where these approaches overlap, it aims at discovering innovative ways in which solutions can be found for problems which have proven so far to be unsolvable in a mono-disciplinary approach.
In computational modeling, theories are formalized in such a way that they can be implemented as computer programs. As a result of this process, more insight is gained into the nature of the theory, and theoretical predictions are, in principle, much easier to develop and assess. With regard to computational modeling of musical knowledge, the theoretical constructs and operations used by musicologists are subjected to such a formalization. Conversely, with computational modeling of music cognition, the aim is to describe the mental processes that take place when perceiving or producing music, which does not necessarily lead to the same kind of models.
Surprisingly, one of the main problems in computational modeling is its success: there is a huge number of models proposed for many tasks in the form of working computer programs. But the psychological validation of these models, their implication for theoretical constructs, their generalizability, and the relationship between different models is often left obscure. Thus, the success of the method is only apparent and a new approach is necessary. Recently a methodology has been emerging in which a working computational model is seen much more as the starting point of analysis and research, than as an end product. This approach needs further elaboration, because it promises a way out of the present stagnation.
Music is an excellent domain for experimenting with this methodology: knowledge about the domain is available at many levels (psycho-acoustic, music-theoretic, historic), and formalization is not as far removed from music itself as commonly thought: consider, for example, the extensive music notation system that has evolved. In human culture, music is as widespread a phenomenon as language, and although the variety of musics of different societies and cultures as well as their continually changing character appears to refute the possibility of formalization, there are reasons to believe that there are basic mechanisms that underlie human perception and performance which facilitate and constrain the genesis of a music, much as they may do in language.
However, music is not an easy domain for developing computational models. Some of the characteristic problems include: mutually incompatible overlying structural descriptions, the combination of discrete and continuous types of information, and the incremental nature of processing that often relies on a combination of both bottom-up and top-down mechanisms. These problems, though, make music a fruitful domain of research, the outcome of which is beneficial to other fields as well.
This proposal concerns the computational modeling of temporal structure in musical knowledge and music cognition. The research is interdisciplinary by its very nature. It not only depends on contributions from different disciplines, but its main objective is to link theoretical as well as practical work from computer science, psychology, and musicology. These disciplines have all been successful in explaining some phenomena of music cognition, although often in ways useful only within that specific discipline. Because they stand so far apart and employ such widely divergent approaches and theoretical constructs, it is hard to have one benefit the other. (N.B. Some terms used in this document have a different meaning in the various disciplines. However, it will be clear from the context which is intended). However, the past decades have shown progress and there is a tradition in the computational modeling of music cognition on which we can build. The work of H. C. Longuet-Higgins, for instance, reflects a successful attempt to cross the boundaries of two of the disciplines involved, namely music theory and AI (Longuet-Higgins, 1987). The availability of implementations of his theories allows other researchers to experimentally test, refine and extend these models in ways formerly impossible.
The aim of our research is to elaborate the scientific instruments, methods, hypotheses and findings that originated in one discipline, in such a way that they become accessible in the other disciplines. The central means, the language, that can make such an undertaking a successful one, is computational modeling. In our work, a computational model is thus not an aim unto itself, but a viable means to compare and communicate theories across different research communities. And although computational modeling is an already well-established method in many fields (e.g., Pylyshyn, 1984; Partridge & Wilks, 1990), the innovative aspect of our research lies in postulating new ways to fulfill the potential of this powerful methodology: to narrow the gap between the disciplines involved.
In music cognition research we are still a long way from fulfilling the promise of computational modeling. Let us start by considering the contributions of the individual disciplines.
First, computational models stemming from cognitive psychology have a clear advantage over verbal psychological theories in that they model cognitive functions in the explicit form of a computer program. These computational models are open to immediate testing, and provide a strong framework for validation or falsification. Unfortunately, these models are often formalized (i.e. programmed) in such a style that formal methods from computer science (e.g., equivalence proofs and formal semantics, e.g., Stoy, 1977) cannot be appropriately applied. However, after a reformalization of the program code (e.g., using meaning-preserving program transformations; Friedman, Wand & Haynes, 1992), many important programs (or models) can be brought within reach of these methods of analysis and can profit from the advantages of computational modeling. More recently, the use of computational models has also become more prevalent in music cognition research (e.g., Bharucha, 1991; Gjerdingen, 1994). This work arose out of a relatively long tradition of research in the experimental music psychology (Deutsch, 1982; Dowling & Harwood, 1986; Sloboda, 1985; Krumhansl, 1990; Fraisse, 1982) in which computational models were less of an issue.
Second, psycho-physics is a research discipline that mainly deals with the peripheral mechanisms for the perception of sound. A vast number of formal models and empirical data is available providing valuable insights in the basic mechanisms of e.g. time perception (van Noorden, 1975; Handel, 1989; Nakajima, ten Hoopen, Van der Wilk, 1991). However, the stimuli used in experiments are often restricted to impoverished data - as seen from the music cognition perspective (see Bregman, 1990; McAdams & Bigand, 1993). The challenge here is to relate the models of psycho-physics to the richer context of music perception and to the models of higher level cognitive processes.
Third, Artificial Intelligence provides another important view on music cognition by constructing working computer models that are well-formalized, and of which the architecture and the behavior are open to analysis. These models address issues that are usually not touched by the other disciplines (e.g., the importance of real time processing, anticipation and planning), and provide important guidelines for successful "real-world" models (e.g., Dannenberg, 1988). However, while algorithms originating from the field of AI often work well (according to their input-output specification), in the program code it is not made explicit where modeling stops and implementation details begin. This makes it difficult to test these algorithms as cognitive models using experimental methods.
Fourth, musicology and music theory provided music cognition research with the theoretical concepts and structural description of the domain of music itself. Here as well, formal theories are being developed (e.g., Cooper & Meyer, 1960; Forte, 1973; Lewin, 1987) that are good starting points for further evaluation and extension. But like before, some characteristics of this discipline make an interpretation in the other disciplines difficult. First of all, programs stemming from musicology usually do not address the incremental nature of processing musical material (they consider a composition as a whole) and evade the problems caused by the interaction of the mechanisms postulated in isolation (like rhythm, meter and global tempo) (see e.g., Balaban, Ebcioglu & Laske, 1992). Furthermore, besides historical studies, musicology mainly concentrates on material as written in a score, ignoring music performance. Although more recently, there is a growing interest in the actual act of making music (building on work from ethno-musicology) and in the use of a more formal framework (Lerdahl & Jackendoff, 1983; Narmour, 1992), the computational aspects often do not rise above the level of tools that support traditional score-based analysis methods. A shift of focus from score to performance can have a major impact on music research, opening the possibility for a more formal and perceptually oriented musicology (see, e.g., Kramer, 1988; Epstein, 1994).
In conclusion, we can see that often one field of research served as inspiration for another (e.g., theories from musicology functioned as a starting point for the formation of hypotheses in experimental psychology, and findings from psychology have had an influence on the design of in Artificial Intelligence programs). But these interdisciplinary influences generally do not extend beyond the level of generating hypotheses and motivation.
In the past ten years, we conducted a number of studies in which a truly interdisciplinary approach was developed (Desain & Honing, 1992a). Although the research covers a range of topics, the central theme in our work on music performance and perception is the relationship between timing, tempo and temporal structure - one cannot be properly modeled without the others. As an example, a motor program that is relationally invariant with respect to global tempo, as is brought forward in studies of motor behavior (Heuer, 1991) and proposed as an explanation for music performance (Repp, 1994), cannot accurately explain the systematic temporal variations (i.e. timing) found when performers play at different rates (i.e., global tempo). We have shown that such a non-structured mental representation falls short in explaining the timing variations observed in music performance (Desain & Honing, 1994b). Our observations led to the exploration of an alternative in which several simple overlying syntactic structural descriptions of the music each contribute to the temporal aspects of a performance (Desain & Honing, 1991b). Our subsequent work found support for the hypothesis that expressive timing is used to communicate the structure of the music to the listener - an underlying theme of all our research. For example, the work showed how the process of meter induction can make use of expressive timing information, an aspect that has never before been modeled (Desain & Honing, 1994a).
In various studies, whenever there were algorithms available, we have investigated the relationship between them and their validity as a model. This required the development of new methods (Desain, 1993; Desain & Honing, 1995), especially when the different computational formalisms used differed widely (e.g., rule-based vs. neural net vs. complex dynamics).
From this work in music cognition a fruitful methodology is now emerging, evolving into a research paradigm, the findings of which have a far wider applicability than the study of music alone. This methodology makes use of a collection of techniques for analyzing and comparing existing computational models, like rational reconstruction and extraction techniques, object-oriented techniques for factoring knowledge, visualizations of abstract qualities of computational models, formal specification of and reasoning about algorithms and meaning-preserving program transformations.
The success of this approach to computational modeling has been recognized internationally and has resulted in several collaborations with researchers from different disciplines in an attempt to make their theories accessible to other disciplines. Our plans are to fully embrace the emerging paradigm, to make it more explicit and to develop it further as a coherent set of scientific instruments.
The proposed studies are grouped according to their perspective on the research: the computational modeling methodology, the music domain itself, and applications of the findings (for a brief overview, see "Summary of the Studies").
Firstly, the paradigm, its methods, tools and problems, will be the topic of explicit methodological studies. They deal with the theoretic and pragmatic aspects of computational modeling.

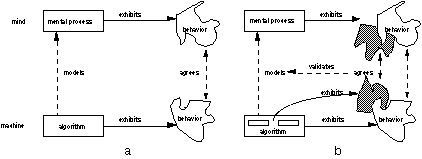
Figure 1. Psychological validation of a computational model.
Before describing the studies themselves, we will sketch the conceptual framework of computational modeling and the constructs involved.
We are interested in the behavior of a human subject (e.g., listener, performer or composer) involved in some task. The subject exhibits behavior, i.e. an observable relation between stimuli and responses (see Figure 1a top). This behavior can be studied (as in experimental psychology) showing relations between the factors involved. Although this approach tells us which factors in the stimulus are relevant for the response, and it can test in which way they influence behavior, it cannot provide a direct explanation of the cognitive process.
In order to find out more about the cognitive process that achieves the task, in the computational modeling approach, an algorithm is constructed that exhibits similar behavior. This turns out to be a difficult task which often consumes most of the research effort. But, in principle, after the construction of a computational model, its behavior can be related to that of the human subject (see Figure 1a). This leads, however, to an interpretation problem: the input and output representation has to be related to the stimuli and responses of the human subject, and reductions and assumptions have to be made because the behavior of the subject is not formalized in itself (Ringle, 1983). But even assuming that a reasonable mapping exists between input and output of the model and that of the human subject, and assuming that the model builder has succeeded in creating an algorithm that exhibits behavior which agrees with the empirical data, we cannot say much about the architecture of human cognition. The fact that the behavior of the two systems agree does not, in itself, validate the algorithm as a model of the mental process. For example, the model builder might have implemented a large lookup table and listed all the stimuli patterns and the appropriate responses. This null-architecture does not explain anything, but it produces the desired behavior.
Therefore, we have to "open up" the program to check what is inside, i.e. look for the congruence of the model and the human subject at a finer scale - a comparison based on global input/output behavior (i.e. functional equivalence) is too coarse to make substantial claims about the psychological validity of the model. If we want to make statements about the architecture of human cognition, we have to somehow relate the architecture of the program to that of the human subject. Take for example an algorithm that decomposes a task in two sub-processes (see Figure 1b). If the program is claimed to be a cognitive model, this architecture is taken to reflect a similar subdivision in the mental processes of the subject. Since it was shown,, in principle, that such an architecture is a viable one (because the program performs well), we now have to show that it is psychologically valid. Unfortunately, we cannot asses this directly (apart from case studies of brain-injured subjects and from brain-scan techniques, which both work only for relatively coarse descriptions of behavior), nor should we aim to proof that the mental processes have a similar modularity. To show this strong equivalence (Pylyshyn, 1984) is, in most cases, not a realistic objective. Since the descriptions are at such a high abstraction level, we can only claim that our model is a psychologically plausible decomposition of the mental processes to some degree and we can show this only in an indirect way.
First, we extend the definition of behavior of the model (see Figure 1b, bottom). For example, incorporating the evolution of internal state over time, amount of input needed before responses can be given, or the complexity of the task for different stimuli measured in calculation steps in accordance with the chosen modularity. Then, we try to define a similar extension of the definition of behavior of the subject (see Figure 1b, top), for example, the response when only part of he stimulus is presented, the time before a response is given, etc. And finally, we have to check the agreement between these extended definitions of the behavior. If the model predicts this extension well, this can be taken as evidence of the adequateness of the model as a description of mental processes. This is especially so, if the predicted behavior is critically related to the proposed decomposition, an issue which is better understood when more models with a conflicting modularity are available for study. In this indirect way, evidence for the psychological validity of the design of a computational model at a certain level of modularity can be collected.
When the modularity of an algorithm is shown to be consistent with the extended behavior, we can proceed to break down the next level of architecture and see if there are ways to verify those empirically. However, a computer program can be broken down into extremely fine building blocks, levels of descriptions of behavior which were not intended by the modeller to reflect anything in human cognition. From the program itself, it is not often clear which aspects of modularity were and which were not intended to reflect the architecture of cognitive processing (the grain-problem; see Pylyshyn, 1979). An important part of our contribution to the computational modeling methodology is to define extensions of programming languages in which these issues can be expressed by the model builder, such that the role of the program as a model can be formalized as well, and predictions are much easier to be made. The results of this first and central methodological study will help in assessing the psychological validity of the individual programs.
Furthermore, we will address the issue of model-model comparisons. The analyses mentioned above will make the relations between different models, and the consequences of the difference in their architecture, clearer. The large variety of incompatible models of music cognition and the representation of musical knowledge, and the unclear link between them, is a real problem in the present state of cognitive science. This problem is aggravated whenever the models are expressed in incompatible computational formalisms. This is a situation found in many domains of cognitive science (see, e.g., Jacobs & Grainger, 1994 for a discussion on models of visual word recognition). Current proposals for models based on continuous (sub-symbolic/numerical) and discrete (symbolic/structural) processing and knowledge representations are almost always studied in isolation, in their respective research communities (e.g., neural net and complex non-linear dynamics vs. rule-based and other symbolic AI). In music cognition research this is common as well (see, e.g., studies on beat induction (this proposal), or tonality). In such a situation, it will remain unclear what a particular paradigm contributes to the ease of expressing the model, whether it is essential to the model's description, or whether it can be considered merely an implementation choice. Such unclarity hampers the progress of cognitive science, that, in the end, needs to make claims about human cognitive processes itself, not to only develop programs implemented in one or the other computational paradigm. It is our experience that the development of an abstract formal representation of the behavior of systems that can be applied across paradigms, yields direct insight on their differences (often smaller than expected) and similarities (Desain, 1993). Once the relations between these types of knowledge and between the paradigms are understood better, divisions into research camps will become less necessary and new progress can be made. These issues will be explicitly addressed in the second methodological study on subsymbolic vs. symbolic processing. It aims at finding ways to describe the internal structure and behavior of these computational models from different paradigms such that they still can be compared.
Sometimes the computational model's modularity is based on constructs outside the realm of cognitive processes, like physical masses and forces. A third methodological study will address the use of metaphor in models of timing, tempo and temporal structure. It focuses on models that give descriptions of musical phenomena based on the metaphor of physical movement. Although these models form a viable alternative to a wholly mentalistic approach, it seems that they sometimes give reasonable descriptions, but no proper explanations of the phenomena modeled. Some areas where this approach can be shown to work, will be elaborated; for others a critique of, and alternatives to, this approach will be given. We hope that this will yield a better insight in the evaluation and validation of models in which the computational machinery is not necessarily an abstract computing device.
In music theory and computer music, the methodology used to express new theoretical constructs or composition principles is often to design a programming language for music (see Loy, 1988). These languages provide relatively complex constructs that deal with, for instance, real-time control, parallelism, and data structures for temporal constraints. However, the underlying syntax and semantics are often developed intuitively (i.e. not in a formal way), which inevitably results in inconsistencies and other problems. A proper and early analysis of programming language constructs (Desain & Honing, 1993a; Honing, 1995) could have prevented these errors, and could have simplified the effort of the music theorist or composer using it. A fourth methodological study aims at identifying the areas where computer music needs special programming languages and constructs (and where it can be avoided because existing languages can be used), and study the existing proposals and their problems. The aim is not so much to design a new language, but to make proposals for improvements and to bring forward general constructs with proper formal semantics, that can be used for existing or new programming languages for music. We will aim to stay as close as possible to recent developments in theoretical computer science (e.g., Abelson & Sussman, 1985; Friedman, Wand & Haynes, 1992; Tennent, 1981; Kiczales, des Rivières & Bobrow, 1991; Winskel, 1993) and make use of that body of research.
Although all methodological studies will build on previous work regarding music cognition (Dannenberg, Desain & Honing, in press; Desain, 1990, 1991, 1992b; Desain & Honing, 1993a; Desain & Vos, 1990 ; Honing, 1993a, 1993b, 1995), the results will now be useful for modeling efforts outside the musical domain (like visual perception, psycho-linguistics and motor behavior) and in general help to provide pragmatic solutions to one of the fundamental problems of present cognitive science.
Domain-studies form the second component of our plan, i.e., developing further the topics of research previously initiated, as well as addressing yet untouched research questions. These studies will deal with the empirical basis and the construction and validation of computational models of music cognition.
The research will mainly focus on the domain of (the perception and production of) musical time and temporal structure (see e.g., Michon, 1975; Povel, 1977; Rasch, 1979; Michon & Jackson, 1985; Vos & Handel, 1987; Handel, 1992; van Noorden, 1975; Ross & Houtsma, 1994)
Temporal structure is a collective term for a number of temporal aspects that play a central role in the cognition of music. We will describe them here, ordering them according to the relationship between time intervals upon which the structure is founded.
In the most general case, we consider the logical structure of time intervals for which only the inclusion relation is defined. This hierarchical part-of relation is used in modeling the organization of memory in so-called "chunks". This level of description is used to open our work to theories of coding and musical analysis. It is impossible to derive any information about time duration here. Furthermore the role or function of a part in a whole is not represented.
Another type of temporal structure arises when the ratio of time interval durations can be decided - on a rational scale. On this time scale, rhythms can be described (independent of the actual performance tempo and devoid of expressive timing). Models of rhythmic coding, beat and meter induction are often defined for data on this (score) time scale.
Temporal structure can also be described on an interval scale, a scale on which the time intervals have real durations. This is the level where performances can be represented and perceived and duration, timing and tempo is studied.
Yet another aspect of temporal structure comes into play when there is a causal relation between time intervals, as is the case in describing mental representations for time keepers and the timing of motor programs.
The different temporal aspects are interdependent and a central aim of the domain-studies is to find out how they relate and interact, and how they can be combined in explanatory models.
We think that temporal aspects in themselves can be modeled relatively well in isolation. That does not mean that perception of music can ignore the interaction of time and rhythm with other parameters, but we will assume that the interaction is organized through quite narrow channels. Other musical processes can provide information in the form of, e.g., chunking based on, a harmonic or melodic analysis. In that sense, we can abstract -for the moment- from what these other processes precisely are, while being able to make use of their output. In the design of computational models we will anticipate possible input from other, non-temporal, musical analyses. We will also open up existing models for non-temporal aspects. For instance, existing models of beat induction based only on temporal sequences and their perceived accentuation (Povel, 1981) will be extended to deal with other kinds of (perceived) accent based on, for instance, loudness or melodic structure.
Because temporal aspects form such a rich domain in themselves and the incorporation of the study of other aspects of music would make this project unmanageable in breath, we decided in favor of this restriction, which will be alleviated somewhat because, as stated, after the study of temporal aspects in isolation, there are ways to link the resulting computational models to modules processing other aspects of music.
Another restriction is that, although performance is a central topic in these studies, we will not attempt to model the "ideal" performer, nor performance style, let alone the golden rule for making good music. Music is very diverse, with an enormous variety of styles. We are interested in the underlying mechanisms that facilitate the perception of timing and temporal structure in all these musics. And while "swing" or "drive" in pop or jazz music differs widely from the way in which the time signature in western classical music is expressed -even within each style expert performers have their own recognizable signature- all the performances rely on the listeners perceptual mechanism that can capture and appreciate the regularity of the expressive timing related to meter. This process is the aim of our modeling effort, and not so much the modeling of specific styles, although these might come out in some cases as specific parameter settings.
In each domain study a relatively isolated phenomenon of music will be studied using the methods and theories of the three disciplines, aiming at a much deeper understanding than would have been possible in a mono-disciplinairy approach. The following research topics will be treated in that way: the modeling of beat induction (this study will take an central place in this project), the internal structure and timing of musical ornaments, the separation of expressive timing into its structural components, and the expression carried by continuously changing parameters (e.g., vibrato and glissando) (Desain, 1992a; Desain & Honing, 1991a, 1991b, 1992c, 1993b, 1994a, 1994b; Honing, 1995).
Thirdly, we will actively pursue practical applications of the evolving theoretical framework. The availability of theories that adequately describe processes of human perception of music make it possible to design better tools for editing musical information in a practical studio or consumer environment. There is a whole range of applications that could benefit from knowledge about musical time and temporal structure - a good theory of music time perception will make possible a far more reliable and natural use of these technologies (in the section "Applications" examples are given). The music industry can benefit greatly from these innovations because all present interactive multi-media applications (a rapidly expanding market) are still based on low level non-structural descriptions of individual events, and exhibit far from intuitive, perceptually and musically sound behavior. And the availability of implementations of these theories makes the design of a product much easier to initiate.
Because practical experience in introducing this technology in products will, in turn, help evaluate (and show the limits of) the theoretical findings, the technological component of this research program is important for the scientific part as well.
The relevant areas of the music industry are: the producers of electronic music instruments (e.g., Yamaha, Roland), developers of music software for professional and home use (e.g., Opcode, DigiDesign), designers of professional recording and editing equipment (e.g., Studer, Polygram), and producers of interactive multi-media systems (e.g., Sony, Philips). Besides the music industry, our research is of relevance for the design of multi-media systems. In order to realize synchronization between image and sound, knowledge about timing, tempo and temporal structure is needed.
The development of applications does not have to wait until the first theoretical and empirical results are obtained in the Pionier project. There are a number of theories, available as programs from previous research, that can be developed into a prototype directly from the start of the project (e.g., Desain, 1986; Desain & Honing, 1988; Honing, 1990, 1992). These applications will be developed and financed outside the Pionier project. The developers, though, will function within the Pionier team and benefit from the expertise and facilities available. We will apply for funds by the Stichting Technische Wetenschappen (STW) and other programs that support transfer between research and industry (e.g., ESPRIT).
The first application is a system with which musical material can be retouched in the recording studio at the (high) level of musical concepts (like swing or rubato), rather than at the (low) level of the acoustical signal.
The second project is aimed at developing a rhythm lexicon. When new media (like CD-i) are used in music applications, the availability of theoretical constructs that allow navigation through huge amounts of data become crucial. For searching a rhythm in a large lexicon, a perceptual similarity measure is indispensable. The same is true in deciding which piece is played and tracking its score in a rehearsal session.
The third application is not a commercial one. The tools designed for our research in music cognition (Honing, 1990) proved to be of such practical value that, after they were provided to colleagues and made available on the Internet, they are now used throughout the research community. It is planned that all new developments will be made available as well. Furthermore, these tools will be extended for educational use in courses on music cognition.
In conclusion, we presented a new and challenging approach to the study of music cognition and the modeling of musical knowledge using three different perspectives. It relies on a close interdisciplinary interconnection between psychology, musicology and computer science. The approach is novel in its breadth and the use of computational modeling as the central methodology. We are convinced that this approach will break new ground in computational modeling, in the sense that it will alleviate the problems that are caused by the multitude of computational models brought forward in cognitive science, frequently presented in different computational formalisms (neural net, rule-based, complex dynamics, etc.). This multitude presently seems to hinder progress. Although starting in the margins of each scientific discipline, namely at the point where it overlaps with the others, the results will be of benefit to the core of the individual disciplines, mostly for psychology and musicology.
We expect that this novel approach to the evaluation and comparison of models of music cognition and musical knowledge will also cause a step forward in the construction of theories about temporal structure. The domain studies will each contribute to central problems in the temporal domain, and, using the techniques of computational modeling, yield generalized models and a better understanding of the issues.
The gains of this project will not be limited to purely scientific progress, as the application of the theories for the development of a better, more musical and perceptually based technology for multi-media will be actively pursued. Thus, the characteristics of the proposal conform with the strategic aims for research recently presented as the policy of NWO: the research is interdisciplinary and it explicitly addresses the development of applications in the development of, for example, multi-media systems.
It may be clear that the research envisioned calls for a large-scale effort. All work is closely intertwined and needs to be properly scheduled. The research needs contributions from musicologists, experimental and cognitive psychologists, computer scientists, and specialists in music technology.
In these studies the methodology of computational modeling is addressed. The issues range from global problems regarding the methodology of computational modeling to the detailed technical aspects of programming itself. Computational modeling of music cognition normally adheres to, and stays within one research paradigm - we will address the larger issue of the research paradigms themselves as well. This will enhance our understanding of the role these paradigms play in the construction of theory, and will yield theoretical constructs that can be used across paradigms.
From programming language to modeling language. This study aims at developing ways to express, in a formal sense, the relation of a computer program to the mental processes it is claimed to model, such that the predictions for empirical studies can be derived more directly from the programs themselves. Formal tools from theoretical computer science will be adapted for practical use in building computational models and in formally assessing their properties. The tools will be tested for the construction of a suite of computational beat induction models (described below "Beat induction").
Programming language design for music. This study deals with existing and new programming language constructs in composition systems and music representation languages, with a focus on the interplay of discrete and continuous data, the flow of data and control in real-time music processing, and the complex issues of the representation of musical knowledge.
Sub-symbolic vs. symbolic processing. The aim of this work is to demonstrate how scientific progress can still be made in (or even, can make use of) the situation where two very different paradigms exist: the connectionist and the symbolic. It will be shown how a theoretical construct of expectancy can function as a representation that enables detailed comparisons of behavior of computational models that go beyond functional equivalence.
Physical metaphors. This study questions the validity of a growing group of models that gives descriptions of musical phenomena based on the metaphor of physical movement. While these models sometimes form a viable alternative to a wholly mentalistic approach, in quite a number of other cases they bring forward only the illusion of explanations of the phenomena of timing, tempo and temporal structure. Critiques of, and alternatives to, this metaphorical approach will be given.
There are a number of domain studies planned (the study on beat induction has already started), for which the research goals and methods will be described. The beat induction study, can be considered the largest and most central undertaking. Starting point for all studies are constructs from music theory and performance practice that are approached using methods from AI and experimental psychology. All studies share the advantage gained from the interdisciplinary approach.
Beat induction. This study entails an elaboration and comparison of a large set of computational models for beat and meter induction stemming from different computational paradigms, an assessment of their psychological validity linked to the incremental nature of the process and the development of a model that treats the advanced issues of persistent syncopation and expressive timing in a better way.
Performance and perception of grace notes. This work's goal is the inference of a typology of grace notes from the dependency of their timing on global tempo, the influence of their existence on perceived local tempo, and the structure of mental timekeepers that control their production as deduced from co-varying time intervals. The typology will be formalized as an object oriented decomposition of behavior and will be compared to the music theoretical constructs.
Separating the components of musical expression. This research will result in a method to split the expressive signal into its structural elements based on a generalization of existing generative models. It will shed more light on the anatomy of expressive timing and dynamics, yielding ways to estimate optimal parameter settings for the models and to estimate the amounts of variation that can be attributed to the different musical structural descriptions.
Continuous modulations. This study focuses on modeling the regularities found in continuous parameter changes, especially in-between notes. The aim of this study is to proceed beyond the identification of perceptual differences and informal discussions of their structure: in modeling these continuous aspects in music performance computationally, we hope to lay down a basis upon which research assessing their role as carriers of musical expression can build.
Last, but not least, one of the advantages of computational modeling is the fact that a working program can find its application in commercial products. Stalled development of editing tools in music studio prompts for fresh solutions that consider the problems from another perspective. Some parts of our research would require a lot of development before products can be designed, but other parts can be applied more or less directly and applications are planned for development at the beginning of the Pionier project. For the first two, additional funding from industry will be necessary; the third is not aimed at commercialization.
Expresso, an editor for expression in the music studio. This system facilitates editing operations that are meaningful at a musical level, and with perceptually sound results. It is based on a calculus of expression that describes how different types of expression are linked to musical structure and how they can be manipulated while maintaining consistency.
Rhythm lexicon. This large database on CD-ROM and the Internet allows the exploration of the space of all possible short rhythmical fragments. The means for easy navigation of this space, based on theories from rhythm perception, are the crucial components. The patterns will be annotated with ethno-musicological information and possibly sound fragments.
POCO, a workbench for research on expression in music. Musical performance data often requires a lot of preprocessing, matching, filtering and tabulation before ,e.g., statistical analyses can be made. Complex processing is needed as well for the generation of musical stimuli and the manipulation of musical data. Tools for these operations are made available in a neat modular form all based on a shared representation of musical data in textual and MIDI file formats. A preliminary version of this system is already available for researchers and is used worldwide. Various parts of POCO will be developed further.
The relevance of the research proposed lies, first and foremost, in the elaboration of the connection among the disciplines. However, as we will describe below, the work will be of relevance to each individual discipline as well.
For psychology it is important that the method of computational modeling functions better in the context of theory building and psychological validation. The early promise of this method is not fulfilled and the gap between the cognitive work, that brings forward these models, and the experimental approach, that should validate them, is huge. In this proposal, several ways to improve methods of computational modeling are presented that will help strengthen the methodological foundations of cognitive science. They will be elaborated, made explicit, and made available in the form of practical tools for the model builder. A central study in this respect will aim at the understanding of how an algorithm can be described formally such that it is not solely a description of a computation, but also entails a formal specification of its interpretation as a partial model of another (mental) process implementing the same computation. Progress in this area will be of direct relevance to cognitive science at large.
Beside better ways to develop new computational models, the need to compare existing models is obvious. Progress in the understanding of psychological processes is, at the moment, hampered by the multitude of models proposed, often expressed in different formalisms. The solution, as we see it, is to progress towards descriptions of behavior that exhibit more detail than pure input/output specification. Expectancy is one such notion that, apart from its more or less traditional interpretation as a psychological factor, can function as a theoretical construct that allows the study of computational models across different formalisms and paradigms (i.e. abstracting from the incompatible state-space descriptions of the different formalisms). And in our view, any approach is worthwhile if it can possibly help prevent the fragmentation of the study of cognition.
Concerning the perceptual studies in the domain of temporal perception, those described in this proposal are relevant for the discipline because they build upon psycho-physical work done on extremely simple stimuli and aim at modeling processes of perception and production of material that is far more ecologically valid. And although we do not claim that the perception and production of full musical material can be addressed, and still make serious reductions as to the extent to which, for example, melody and timbre interacts with beat induction, we think we can propose ways to model phenomena above the level of strict mechanical temporal patterns.
Furthermore, even for music psychology, which has been quite an academic community, the time has come to see to what extent the theoretical findings can help in the development of products - or even give rise to completely new ones. It would be a pity to let the opportunities to participate in, and benefit from, the multi-media industry pass by, even when the primary aim is one of understanding of the wonderfully complex human mental capabilities needed to appreciate music.
For musicology the proposed research opens up a new line of inquiry, a basis for a new style of musicology where musical structure as expressed in performances is the central object of research, and not so much the musical structure of the score. Current developments in music theory (e.g., systematic musicology) indicate that the time has come for a musicology that is more perception and performance oriented. The fact that information about the musical structure can be extracted from performance information (e.g., Clarke, 1988; Palmer, 1989; Repp, 1990), makes it possible to support theoretical work with empirical findings from music psychology. We will proceed in this direction with two studies that relate expressive timing and musical structure. One domain study will show how different types of musical structure (phrase, meter, local) can be traced back from the expression in a music performance. The domain study on grace notes will show how the timing of these ornaments can be used to distinguish between the different music-theoretical roles they have. However, not all musics are made out of discrete note events, and the methods for studying of aspects like expressive timing, that have been developed for keyboard music, cannot be used. The expressive possibilities of instruments that allow continuous modulations in pitch, loudness and timbre are much more complex. The study on the continuous modulations in music performance provides way of systematically analyzing, formalizing and modeling them. It will contribute the tools (for use by, e.g., ethnomusicologists) that would make it possible to construct theories for expression carried by the continuous aspects of music. This is now a rather unexplored area, although it is generally agreed upon that dealing with both the discrete and continuous aspects of music is crucial in understanding its full complexity.
The studies on performance, mentioned above, will show how the theoretical constructs developed in musicology can find an empirical basis in music performance. But also the theoretical constructs themselves are the topic of investigation. Musicology has a strong tradition in building formal accounts of the structure of music. Presently, the generative theory of Lerdahl & Jackendoff (1983), inspired by the work of Noam Chomsky, and the cognitively motivated "implication-realization" theory of Narmour (1992) deal with the full complexity of notated music and describe musical analysis in the form of more or less formal sets of rules. However, these theories do not formalize all aspects of the analysis process (like the interactions between rules) to the extent that they could be called computational models and could run mechanically: a large role is left for the music analyst in interpreting and applying the theory. The second way in which this proposal is relevant to musicology lies in a refinement of the formal basis of these theories for some limited aspects of music. A joint study with Lerdahl on beat and meter induction will aim at a further formalization of this part of his theory, such that it will become a computational model. In general, the discipline will benefit from the new methods and analysis techniques that come with computational modeling, enabling the development of a mature computational musicology.
A third, more practical spin-off of our work will be the study of tools for composers and computer musicians, especially in the realm of algorithmic composition (where musical expression has been largely ignored) and real-time interactive composition (where cognitive theories can help in providing a solid basis for the design of listening machines). Although the direct development of these tools is not an aim in this project, the study of its foundations (in the study of programming language design for music) will contribute to a better scientific basis for this field.
Contributing in a fundamental way to computer science is not an aim of the project. However, besides the promotion of the use of tools and formal methods from computer science for application in the other disciplines, the studies may well contribute some fresh ideas to the science itself. The study in which this will be most visible is the development of programming language constructs for cognitive modeling. In technical computer science, whenever there is a system modeled (or simulated) by an algorithm, the relation of the parts of the algorithm to the parts of the physical system is often trivial, and the assessment of the validity of the algorithm as a model is not such a difficult problem as in modeling systems (mental processes) of which the structure and internal information flow is not observable. However, the idea to extend programming languages such that the interpretation of its architectural parts as a model of a calculation can be formally expressed (as described in the first of the methodological studies), might well have importance for computer science at large: it is not only in cognitive modeling that there are processes whose internal structure cannot be observed. In the study, we will build as much as possible upon existing (procedural-, data- and control-) abstraction mechanisms, and use formalisms for specification and typing from theoretical computer science, in order to facilitate an easy communication of the results back to this discipline.
The second study with direct relevance to computer science is the study on programming languages for music. There are many non-trivial problems in representing music and its processing (like multiple incompatible structural descriptions, real-time processing constraints). These problems are so difficult that their direct expression in a general programming language is beyond what we can ask of composers and musicians. Many proposals for programming languages for music (or extensions or libraries) have been proposed. Some are commercially available and widely used (Loy, 1988), and even serve as the main programming language in academic courses on computer music. However, since many of the constructs in these languages were designed on a more or less ad-hoc basis, they often exhibit semantic inconsistencies, e.g., in handling the intertwining of flow of data and of control, and in the design of binding and scoping regimes. Our study will undertake a critical evaluation of these languages, propose possible repairs, and make the coherent treatment of the design of programming language constructs for music explicit, which may well lead to proposals that will be beneficial to computer science at large.
Next to theoretical computer science, the project is relevant for information technology. In the rapid growth of multi-media applications there is a real demand for methods that can synchronize and fit pre-composed music to fixed video fragments. The automation of the recording studio asks for sophisticated methods to re-synchronize and edit independently recorded tracks of music. Modules that implement theories of musical expression in a robust way will contribute to these developments. The entertainment industry, and its use of virtual reality environments, will need proper methods of performance analysis to control and move objects and animated figures consistently to music. A good beat induction algorithm will be crucial to further these lines of technological development.
It may not be directly clear how the proposed studies are interconnected, apart from their common basis in our general approach to computational modeling and our focus on performance. Though, admittedly, these studies cover a wide range of topics, they have is a coherent structure, and we are sure that the links between them will strengthen the individual studies and that the width is essential to be able to realize the power of the proposed approach.
The long-term aim of the domain studies is to develop models and tools that could form the basis for a new type of musicology. A musicology where music performance is subject of research, not so much the score. The domain studies concentrate on just a few aspects of music performance and perception, they are carefully chosen to deal with independent topics: the analysis of discrete local structure (grace notes study), discrete global structure (like phrase and metrical structure in the separation of expressive components study), and structure in local continuous modulations, as well as mechanisms for inference of structure (beat induction study). But even here cross-connections exist, for example:
There are interdependencies between the methodological studies as well:
But the main interconnections are between the domain studies and the other ones (see Table 1).
Domain Methodological Applications
Modeling Program. (Sub)- Physical Expresso Rhythm POCO
language language symbolic metaphor lexicon
Beat 1 3 8 6 7
Induction
Grace 2 5 7
notes
Separating 4 5 7
expression
Continuous 2
modulations
Table 1. Main cross-connections between studies.
For scientists in general, it can be considered an obligation to make the results of the work (especially when funded by public money) accessible to a large audience, ranging from colleague researchers and students entering the field to interested laymen. The domain is extremely well suited to communicate the work done in cognitive sciences to the general public, since music is performed, composed, and appreciated by so many.
But let us start with the dissemination to the research community. Besides the normal scientific output in the appropriate journals, we plan to help colleague researchers use the tools provided in the POCO environment by organizing a small (2 day) workshop. The Pionier project seems a good opportunity to propose to organize one of the bi-annual Rhythm Perception and Production Workshops (from which our research has benefited so much in the past). The possibility of organizing a "Winterschool" on computational modeling at the KUN will be investigated as well.
Next to these activities for colleagues, we plan to prepare a number of books, directed towards students, which may need to start again at the introductory level when moving from their own discipline into this highly interdisciplinary domain. A book on Lisp programming and modeling is currently written as a textbook for students (Desain, in preparation). A book on the computational modeling of beat induction is planned for the last year of the project. It will collect the joint papers of the beat induction studies, generalizing from them and presenting all algorithms in easy accessible form for educational use. Whether the results of the methodological studies will reach such a mature form that they too can be bundled in a book on computational modeling for students in the cognitive sciences, is still an open question.
Aimed at again another audience, i.e. computer music composers and musicians, we plan to organize a specialized workshop on music composition languages in collaboration with Gaudeamus. Our work will be made available as well to this group via the infrastructure of usersgroups, workshops and software distribution set up by IRCAM (Paris, France).
Furthermore, we will disseminate the findings and results of the research through an Internet/World-Wide Web site dedicated to the computational modeling of musical knowledge and music cognition (a very first setup is currently accessible as http:/mars.let.uva.nl/honing/welcome.html). It will make software, articles, demonstrations and musical data directly accessible.
Finally, we will look for opportunities to present our work in educational context. For example, the Boston Computer Museum showed interest in putting our interactive installation to beat induction on display, such that visitors can play rhythms on a drumset, hear a variety of models respond, and learn about the process of beat induction. We will look for other opportunities as well to communicate the research to a larger audience (through television, radio or special presentations). A form that proved particularly well suited for this means is an overview article presented in the form of a story, as was tried in (Desain & Honing, 1993b). This exercise will be repeated for other topics as well.
In these studies the emergent methodology is made explicit. The issues addressed range from the fundamental problems of the methodology of computational modeling to detailed technical and practical solutions. The consequences of the underlying computational research formalisms and paradigms are addressed in a study on sub-symbolic vs. symbolic computation and in a study on the use of physical metaphors in modeling cognition.
Ideally, a computational model should form a bridge between AI and experimental psychology. On the AI side, the program would be developed to perform a certain task and within the field of psychology the same program would be interpreted as a model of human cognition and its mechanisms would be tested for psychological validity. Both sides have different aims. For technical AI, a computer program should perform well and even the use of an unintelligent tabular or exhaustive search method is not a priori excluded. For psychology, other objectives exist. It is desirable that the program has characteristics (other than input-output relations) that reflect the properties of human cognition as well. Since a formal model exists as a means of communication among the disciplines, and objective formal assertions can be made, one would think that the issues can be easily determined. However, this is not the case. The gap between AI and experimental psychology is huge, although some progress has been made in bridging it (Jacobs & Grainger, 1994; Newell, 1990; Kosslyn, 1994; but see also Brachman & Smith, 1980; Wilks, 1990).
We think the main reason for this gap is the fact that computational models tend to be expressed as a program in a general programming language, and no further formal description of its state as a model is available. A programming language is not a modeling language, and the availability of an implementation of a theory does not necessarily make it clear what predictions about human performance follow. From the program itself, it is generally not clear which aspects of modularity were and which were not intended to reflect the architecture of cognitive processing (the grain-problem; see Pylyshyn, 1979).
As an example of such under-specification, consider a neat and elegant program that is presented as a model for some cognitive task. Though the higher levels of this description may be intended to reflect mental information processing constraints, stating how different sources of knowledge are grouped and transformed in abstract terms, the lower levels unavoidably have to formalize low level details, which may not reflect any serious commitment to the nature of those kinds of processes in humans. Many choices have to be made at this low level (procedural vs. declarative, choice of data types, etc.) that are made on the basis of availability in certain languages, ad hoc efficiency concerns, serial nature of the underlying machine, and other reasons. In that sense a program could even be considered an over-specification.
We propose to develop constructs that would permit the expression of the fact that modeling stops below a certain level, and consider everything below that level implementation detail. This issue is generally not made explicit in computer programs. Measurements of, and reasoning about such variables as the computational complexity and memory load becomes useless when they are not abstracted from low level aspects. The elegant abstraction mechanisms developed in computing science (data-, procedural- and control abstractions) form the beginning of a solution. They can be annotated with assertions about their role in the interpretation of the program as a model.
Consider, for instance, the naive ease with which statements in a program are ordered sequentially, simply because that may be the only possible way in a specific programming language. This means that information is lost about the nature and dependencies of stages in the processing. Statements may indeed critically rely on computations done in order, and a sequential ordering is explicitly meant. But others may be logically independent, they don't need information computed by predecessors and could be assumed to happen in parallel when interpreted as a (mental) model. However, they may still be ordered sequentially because of implementation-dependent multi-process overhead costs. A simple annotation, allowing the author to express these differences, may suffice here.
Another problem that arises when using a program as a formal specification of a model is the modularity that enables a neatly factored and modular description of complex behavior may not be a realistic representation of mental processing, nor of an optimal algorithm. One needs to be able to annotate parts of programs stating that the modularity at that level of design is not to be taken seriously in predictions about, for example, computation load, and the intention is to freely allow any transformation (e.g., to merge computations from different modules) that leaves the program semantically invariant.
A related issue is the fact that sometimes processes can only be described by means of a constraint on the input-output behavior, but no detailed processing can be modeled. This is, for example, the case in models of beat-finding (Povel & Essens, 1985) that predict the metric mental framework that will be induced by a cyclic rhythmical pattern, but it is not intended to model the process of how that percept develops. Presently, we are not expressing these issues formally in our programs, all such information, critical to the interpretation and testing by experimental psychology, is missing. However, the formal specification languages developed recently (Partsch, 1990) could, in principle, provide solutions to this problem.
In SOAR (Newell, 1990; Laird, Newell & Rosenbloom, 1987), a cognitive modeling language that formalizes cognition as goal-directed problem solving, a solution to this problem is attempted. The design of SOAR supposedly reflects many characteristics of human cognition. ACT* (Anderson, 1983), a production system based on the assumption that knowledge is initially proprositional and procedures can be derived from these propositions, has a similar goal. Our proposal is, when compared to SOAR and ACT*, more open. While the aims are similar, we do not go so far as to postulate a fixed cognitive architecture but rather aim to develop formal constructs that can be added to existing programs to formalize their interpretation as a cognitive model.
In the first stage, an inventory of the needed constructs will be made and a semi formal language of annotations will be designed. Expressions in this language can be added as comments to existing programs. We will use a large suite of beat-finding algorithms from different computational paradigms that was developed in previous research (Desain & Honing, 1994d).
In the second stage the constructs will be integrated into the language itself (such that they can be checked for consistency, handled automatically, etc.). The Meta Object Protocol of the Common Lisp Object System (Kiczales, des Rivières & Bobrow, 1991) provides the means to do this easily. It will provide psychologists with an extended programming language in which modeling aspects can be expressed formally and added to the algorithm. In this way it becomes a bit easier to reason about (as well as derive predictions of) task complexity, reaction times, memory load, error rates, etc.
A second part of the research will explore the use of formal algebraic methods in the construction and verification of these computational models. One would expect that psychologist would welcome help from systems and formalisms that allow (automated) reasoning about computer programs. However, the programs proposed as computational models are often so unstructured and lack the use of abstraction mechanisms, that they are placed out of reach of the formal methods available for reasoning about algorithms. And it is a waste to not to make automated reasoning about programs possible. They can provide help in proofs of equivalence. And semantic equivalence is of course not only a practical issue. Often the question how different computational models really are can, in the end, only be answered by formal reasoning about them. They can also help with semantically invariant transformations, specification checks, automatic program construction, and optimization (Partsch, 1990; Rich & Waters, 1986).
As an example, consider the design of a program that checks whether the leaves of two trees are the same (e.g., the notes of two different music-analytic trees or the words in two syntactic structures). The most simple and elegant program would modularize the task into a "flattening" of the trees, and then compare the resulting lists. But this program is essentially inefficient: both trees are flattened completely before a difference in a first leaf may be detected. The program that avoids this inefficiency walks through both trees at the same time, maintaining an administration for both and effectively merging the flattening and equality test programs. This program would predict processing times that are much more closely related to the essential complexity of the problem at hand, and optimality can be proved. However, merged, non-modular programs are notoriously difficult to write and maintain. A third solution does require more knowledge of AI programming constructs. Instead of subjecting both trees to a flattening operation, a process (stream, generator) is created for each tree which can deliver the next leaf when asked to do so. These processes are asked to produce a leaf each and upon successful comparison the process is iterated. Now all three implementations are semantically equivalent; they will yield the same answer, but predictions on time and space complexity will differ. The complex algorithms can be derived (almost) automatically from, e.g., the simplest one when a proper programming style is used. So by programming in this style the model can, on the one hand, be a neatly factored and modular description of complex behavior, and on the other hand, be subjected to automatic reasoning that extracts essential characteristics of the complexity of a non-modular, optimal algorithm.
It will be investigated in which form tools from theoretical computer science (like program transformations) can be made available for psychologists modeling cognition. In some case the programs themselves can even be synthesized directly from their specification. This work will build upon leading-edge research done at Stanford (see Smith, 1990).
The tools will be made available in the Lisp CLOS environment. They can help in extraction or "micronization" of large published programs, a technique often used by us for understanding and comparing existing computational models and systems (e.g., Desain, 1991; Honing, 1995). They are especially useful when code has to be lifted from an obsolete language or implementation to a new one, as was the case in the study of a complex program brought forward by Longuet-Higgins as a parser for musical rhythms (Desain, 1991). The formal tools help in keeping semantics invariant while disentangling control structure, making binding and scoping regimes explicit, clarifying and stripping the code, separating implementation aspects from central representational notions, applying different types of abstraction and other modifications which can increase the modularity, transparency and parsimony. Of course, these methods are no cure for all models, and the application of a formal approach in general, is still difficult for large and unstructured programs. However, frequently a formal method, which cannot be applied in general to programs in a certain programming language, is applicable in the specific case of one program(part) that does not use all constructs of the language or happens to avoid the pathological cases.
In conclusion, both parts of this study aim at adopting current methods from computer science to further the construction of computational models in a style which helps in validating them as models of cognition and brings the tools for a formal treatment of them (in transformations and comparisons) within reach.
Music invites formal description. There are many obvious numerical and structural relationships in music, and countless representations and formalisms have been developed (e.g. Balaban, 1989; Mathews, 1969; Roads & Strawn, 1985; Roads, 1989). When a music formalism is implemented as a computer program it must be completely unambiguous, and implementing ideas on a computer often leads to greater understanding and new insights. Many programming languages were developed specifically for music (Loy, 1988). These languages strive to support common musical concepts such as time, simultaneous behavior, and expressive control. At the same time, languages try to avoid preempting decisions by composers, theorists, and performers, who use the language to express very personal concepts. The domain of music is full of wonderfully complex concepts whose precise meaning depends on the context of their use, their user (be it composer, performer, or musicologist) and the time in history of their usage. It is difficult to capture these meanings in clear, formal representations that can be treated mechanically, but still reflect as much as possible of the richness of the domain constructs and their interplay.
Languages are a measure of our understanding. Our ability to design good languages for a particular domain (such as music) depends upon our ability to clearly describe the terms, conditions, and concepts of the domain. Studying prototypical examples of musical concepts and their natural, intuitive behavior is a good starting point for the recognition of the properties that representations for music should exhibit (Dannenberg, Desain & Honing, in press; Honing, 1995). Once representations can be designed that, on the one hand, do not reduce music to some simplistic and rigid constructs, but, on the other hand, can be defined clearly and formally such that their behavior is predictable and easy to grasp, then their use in composition systems, analysis tools and cognitive models will be quite natural.
So far, we have mastered some of the concepts and provided good support for them in a number of languages (Dannenberg, Desain & Honing, in press). Other concepts are not yet well elaborated in music languages, and are only supported, if they are supported at all, in an inconsistent way. We think that these problems arose out of an unfamiliarity of the designers with formal semantics of programming languages (Stoy, 1977), and, in general, the more formal approaches to programming language constructs that have appeared (Cardelli & Wegner, 1985; Tennent, 1981; Watt, 1990, 1991). Still, these systems often embody a particular solution to a difficult representational or computational problem, that is worth making explicit.
As an example consider the need for data-flow languages constructs for real-time, asynchronous processing in real-time music composition systems as are proposed e.g. in Max, (Puckette, 1988; see Desain, Honing et al., 1993 for a critique). This language, though containing major inconsistencies in the intermingled flow of control and data, is used widely as a first course in programming in educational contexts. This poorly understood topic, and other problems, indicate that the representation of music still poses a major challenge to language design.
We will proceed from studying existing languages for music, like Max, to more general representational problems and address the issues as a search for good abstract programming language constructs that rise above the level of the individual languages. The proposed solution can then be used in the context of existing or new languages for music.
But first we need to start by gaining a thorough understanding of the musical programming language in question. However, since rarely a formal specification of syntax or semantics is given, it is not a trivial task to get a grip on the essential mechanisms and objects of these languages. Often these systems are documented and there are running versions of them available and sometimes even the source code of a compiler or interpreter is given. These can form an indirect entry into the study of the language itself. There are different computer science techniques available that can be used for the analysis of such relatively large programs. A method used in the evaluation of large artificial intelligence systems is rational reconstruction (see, e.g., Riche & Hanna, 1990). The idea is to reproduce a program's behavior with another program, which is constructed from descriptions of the important aspects of the original. The analyses can then be based on this re-formalized version of the system, which is often easier. The technique of micronization or extraction, making a micro-version program from a larger system, is an attractive alternative to a full reconstruction.
Such a micro-version or micro-world is a solid basis for further exploration. It defines a subset of the language, which forms in itself a relatively complete set, but small and easy to comprehend, of essential mechanisms. These stripped versions of the original languages and systems will enable the use of formal techniques, e.g., of programming language transformation techniques (see, e.g., Friedman, Wand & Haynes, 1992). Then a definition of the semantics of the programming language constructs can finally be formalized, possibly in purely functional terms (using the well-understood lambda calculus; Barendregt, 1981).
As an example, the debate on the ill understood syntactic and/or semantic differences between Nyquist and GTF (Dannenberg, 1992; Desain & Honing, 1992d) was solved by applying this method, which finally yielded a lambda calculus description of the different underlying binding regimes which are responsible for the differences in behavior (Honing, 1995). This showed that, again, in contrast to popular belief, a thorough formal definition will make it easier to propose an elegant syntax and intuitive description of the semantics even for layman users of the language (Hall, 1990; Bowen & Hinchey, 1995).
Next to analyzing existing programming languages for music and trying to repair their inconsistencies, the understanding of the issues involved (e.g., about the consistency of continuous and discrete information, the constraints of the body-instrument system, the representation of plans and anticipation of future input) will be used for the elaboration of new constructs directly - as was done for generalized time functions (Desain & Honing, 1992c) and stochastic composition processes (Desain & Honing, 1988). These results will be made available to a wide audience by incorporating them into the Patchwork environment of IRCAM, Paris (Laurson, Rueda, Duthen, 1993).
In collaboration with Gaudeamus, we will seek to disseminate the results obtained back to the community of composers and musicians who were the prime inventors and designers of the existing composition languages and systems. This will probably take the form of an intensive two-day workshop linked to one of the contemporary music festivals.
The so-called Good Old Fashioned Artificial Intelligence has been firmly established in the past decades as a research methodology. Its methods and tools are symbolic, highly structured representations of domain knowledge and transformations of these representations by means of formally stated rules. These rule-based theories can function (and are vital) as abstract formal descriptions of aspects of cognition. However, some authors go beyond that and claim that mental processes are symbolic operations performed on mental representations (see Fodor, 1975). Until the connectionist paradigm emerged there was no real alternative to that view. But now, in this new paradigm, the departure from reliance on the explicit mental representation of rules is central, and thus the conception of cognition is fundamentally different. Connectionism opened up the possibility to define models which have characteristics that are hard to achieve in traditional AI, in particular robustness, flexibility and the inherent possibility of learning (Rummelhart & McClelland, 1989). The popularity of the connectionist approach brought forth much interesting work, also in the field of music (Todd & Loy, 1991), although many researchers lost their objective attitude impressed by the good performance of some (prototypical) models. A connectionist model that "works" well, does not necessarily lead to scientific progress, when questions like the sensitivity to parameter changes, the scalability to larger problems and the dependency of the model on a specific input representation, cannot be answered. Against the background of the debate within AI and cognitive science on the role of connectionist models, careful examination of the weak and strong points of both symbolic and neuro-computing is still needed.
In previous research, this issue was explored by studying two systems for the quantization of performed temporal sequences (Desain, 1993). In that study, a symbolic parser (Longuet-Higgins, 1987) was compared to a connectionist quantizer (Desain & Honing, 1989b). Through the use of abstract descriptions of behavior (and visualizations thereof), it could be shown how the models differed. This line of research will be continued in the beat induction study for a symbolic model (Longuet-Higgins & Lee, 1982) and a sub-symbolic one (Desain & Honing, 1994c). The general approach taken in these studies will be made explicit and applicable to other domains. With the possibility of a comparison of the behavior of these different models, the precise role of the choice of formalism might become clear. Is it central to the description of a computational description of the process or simply an implementation choice? In this study, it will be investigated which notions that abstract from the particular formalism (e.g., from its input/output format, control and data structures) can give insight into this question. It seems that the computational notion of `expectancy' is a good candidate that allows a more abstract description of behavior. This notion formalizes how the internal state built up in the system while processing part of the input (be it the position in a symbolic search tree or the set of activation levels of the cells in a neural network) influences the treatment of new data. Expectation is a function of the input and its result is stated in terms of the input and output format as well. It is a characterization that, on the one hand, probes deeper in the model than simple input-output characteristics and percent-correct scores do, while, on the other hand, states this knowledge in terms of the input and output and not in terms of the states themselves (which are incomparable for models from different paradigms). Furthermore, it allows formalization of the incremental, temporal nature of models of processing. This approach has already proved successful in quantization (Desain, 1993), but it has to be formalized and extended as a more general method.
Ultimately, the big challenge in this theoretical study is to find abstract descriptions of behavior that can be applied across paradigms, and even to find ways to unify and generalize existing, partially successful theories that exist in these different paradigms.
In music theory, when one talks about rhythm, timing and tempo, often the analogy with physical motion is made. For example, in comparing tempi one uses terms like walking or moving. And to characterize the progression of music (be it harmonic, melodic, rhythmic or timing wise) the notion of motion or flow is frequently used. In music psychology the physical metaphor is abundant as well, and has inspired new theoretical results. For example, in the work of Large (Large & Kolen, 1994) the human ability to track the tempo has been modeled as a resonator, using the theory of non-linear coupled oscillators. Apart from a reasonably performing model, this introduces new ways to describe the behavior of these models mathematically. Still, the predictions of the model have to be checked for psychological validity and compared to the behavior of other models (as proposed in the study on beat induction).
But indeed, the wholly mentalistic approach to music perception and production that AI researchers often tend to take, i.e. modeling the process as an abstract parsing or generation process based on explicit mental syntactic representations, needs to be complemented by theories that are much more based on the physical properties of the human body in interaction with a musical instrument. This direction views human movement and gestures in music performance as embodiment of musical thought (Clarke, 1993; Davidson, 1991) and thus views the similarity between musical expression and human movement as necessity - not a metaphor-and in that way proposes a healthy alternative to the abstract mentalistic approach. Furthermore, physical constraints can be observed in the performance signal. The restrictions that the system of musician and instrument impose on a performance (e.g., the influence of distances between string positions in guitar playing), and the effort involved to get the desired result are audible. It might well be that the hypothesis that musical expression is communicating abstract musical structure, needs some amending in which the body-instrument expression is recognized as well as a source of music appreciation. Note that the abstract and often inaccessible nature of computer generated music may well be caused, at least partly, by ignoring these constraints - there is no sense of an instrument being played. And it is the same lack of appropriate constraints that will give away a studio musician who tries to imitate a guitar on a keyboard synthesizer. The results of the few composers who have tried to capture these aspects in their composition algorithms, however unsystematic, have proven to be immediately effective (e.g., Garton, 1992). We will explore these aspects using a generative approach as well. In the study on a programming language for music, a formal language will be developed that enables the expression of these constraints in a systematic way and that allows retrofitting to existing composition systems. In this language, we will assume that allocation of body and instrument recourses is known and given (e.g., fingering, choice of strings and bow direction) and find ways to express how these cause deviations in expressive musical attributes.
Although the physical metaphor can be very useful, as argued above, we have to be cautious as well. The attractiveness of the analogy (e.g., it directly fits a large amount of the terminology used in music theory and performance practice) and the "naturalness" of the explanation, may fool the investigator. The fact that a model has such a basis does not in itself make it a better model. It may give a good description of the data, but it, in principle, does not teach us anything about the underlying mechanisms. A good approximation is not necessarily a good explanation. And to either validate or falsify these models as models of the underlying perceptual mechanisms, more data and arguments need be brought to bear than has been done by the proponents of the physical motion theory.
Sundberg & Verillo (1980), for instance, make the analogy between the performance of a final ritard (the typical slowing down at the end of a piece) in piano music as alluding to stopping after running. Based on a model of a physical mass under constant deceleration, parabola-curves are fitted through measured tempi in piano performance of pieces from the baroque period. Kronman & Sundberg (1987), Feldman, Epstein & Richards (1992) and Sundberg & Verillo (1995) make the same parallel between musical performance and physical motion. Feldman, Epstein & Richards (1992) measured beats in recordings of music from a wide range of periods and styles. They propose a model of musical "motion" in which the progression of music over time is conceived of as being controlled by the mental analog of a mechanical force. Todd (1993) even relates expressive timing directly to the functioning of the vestibular system, the human sense of acceleration that stems from a small organ located in the ear. He argues that "the reason why expression based on the equations of elementary mechanics sounds natural is that the vestibular system evolved to deal with precisely these motions" (Todd, 1992).
In this paradigmatic study we will clarify these questions and evaluate how far this family of physical motion models go in providing a real explanation by reinterpreting earlier studies and empirical data (e.g., Sundberg & Verillo, 1980). Because these models form a subclass of all models that use some sort of global continuous description of timing, independent of rhythm and global tempo, we will first bring to bear the methods of testing the psychological validity of continuous tempo curves developed in earlier studies (Desain & Honing, 1994b). Secondly, we will look at proper physical motion theories and re-evaluate the data for which they been proven to form a reasonable approximation. For these examples, we will provide methodological critique and alternative explanations.
For these parts of the study we will restrict the analyses to studies of the final ritard. We suspect aspects not addressed by the physical motion models play a key role in the nature of the ritard; we expect a dependency between the structure (rhythmical and metrical) of the material, the global tempo and the shape of the ritard.
Considering the rhythmic structure, a ritard of many notes of equal (score) duration can have a deep rubato, while a ritard of a few notes, with possibly a more elaborated rhythmical structure, will be less deep. This is a necessary consequence of the need to leave the rhythmic interpretation intact (not to break the rhythmic categories) while decelerating fast. Models of tempo tracking and rhythmic quantization (e.g., Desain & Honing, 1989b; Longuet-Higgins, 1976) will necessarily predict at least the borderline case for which the rhythmical structure can still be perceived. Apart from explaining the dependency of a ritard on the material played, this will yield a constraint on the form of ritards. Such restrictions are not made by a physical motion model, since any metaphorical mass, force and amount of deceleration is equally likely. We expect the final ritard to only coarsely resemble a parabola, the detail depending heavily on the rhythmical material in question. This may yield an explanation for the common musician's intuition that music from different composers and style periods require different final ritards to work well musically (Clynes, 1987).
Considering the metrical structure, these perceptual models may very well predict a more or less stepwise deceleration, directly linked to the meter of the piece - a phenomenon that has been observed informally (Clynes, 1987) but that could have never been predicted by a physical motion model.
Considering the global tempo, the course of evolution of a physical motion model is fully described by its parameters (mass, deceleration force) and its initial condition (velocity), and therefore these models predict a simple relationship between the shapes when ritards are started at different points in the piece and at different initial tempi. Because their internal state is much more complex, models based on, for example, rhythmic expectancy predict different forms depending on the initial tempo and the starting point. The Beethoven data collected for (Desain & Honing, 1994b) is well suited for an investigation of this relationship.
Although this study has an empirical part, it is aimed at clearing the confusion caused by this popular paradigm. While a physical motion metaphor is perfectly acceptable as a concept for a musician in talking and thinking about music, there are limitations of these models as to the explanation of music perception and production, and sometimes better alternatives exist. These alternative explanations may be complementary to the physical motion theories, because they explain properties of music performance directly from the musical material and the perceptual processes themselves. We are convinced that music is based on, plays on, and makes use of the architecture of our perceptual systems, and that perceptual theories, in principle, can go quite far in bringing forward explanations of the many subtleties involved in the performance of music. However, it is sensible to use the physical motion approach wherever it can contribute to our understanding of musical expression, and to precisely investigate the consequences of the claims made by the proponents of this approach. Finding appropriate terminology and ways of debating these issues, is another aim of this study - the issue is too important to be blurred by paradigmatic battles based on misunderstandings.
The domain studies deal with the empirical basis and the construction and validation of computational models of music cognition, concentrating on the perception and production of musical time and temporal structure. They aim at the development of models and tools that could form the basis for a new type of musicology: a musicology where music performance is the subject of research, and not so much the score. The starting point for all the studies are constructs from music theory and performance practice that are approached using methods from AI and experimental psychology. All studies share the advantage gained from the interdisciplinary approach.
The following topics will be described: the modeling of beat induction, the internal structure and timing of musical ornaments, the separation of expressive timing into its structural components, and the expression carried by continuously changing parameters.
Beat induction is the process in which a regular isochronous pattern (the beat) is activated while listening to music. This beat, sometimes tapped along by musicians, is a central issue in time keeping in music performance. But also for non-experts the process seems to be fundamental to the processing, coding and appreciation of temporal patterns. The induced beat carries the perception of tempo and is the basis of temporal coding of temporal patterns (Povel, 1981). Furthermore, it determines the relative importance of notes in, for example, the melodic and harmonic structure. Meter adds hierarchical subdivisions of time above and below the beat level. Some of the models address the full issue of meter induction, others focus on the beat level only. We will use the term beat induction loosely referring to both aspects.
There are a number of aspects that make beat induction a process that is hard to model computationally. Beat induction is a fast process. Only after a few notes a strong sense of beat can be induced (a "bottom-up" process). Once a beat is induced by the incoming material it sets up a persistent mental framework that guides the perception of new incoming material (a "top-down" process). This process, for example, facilitates the percept of syncopation, i.e., to "hear" a beat that is not carried by an event. However, this top-down processing is not rigidly adhering to a once established beat-percept, because when in a change of meter the evidence for the old percept becomes too meager, a new interpretation is induced. This duality, where a model needs to be able to infer a beat from scratch, but also to allow an already induced beat percept to guide the organization of more incoming material, is hard to model. This might be an explanation for the wide variety of computational formalisms that have been used to capture the process. In Table 2 an overview of the approaches is given.
Progress in beat induction research is stagnating because the proposed models are described in a variety of formalisms, which makes them difficult to compare. Another problem is that the models implicitly address different aspects of the beat-induction process. For instance, some models explain the formation of a beat concept in the first moments of hearing a rhythmical pattern (initial beat-induction), some model the tracking of the tempo once a beat is given, and others cover beat induction for cyclic patterns only. To stimulate exchanges between these approaches, we organized an Email platform (Desain & Honing, 1994e) and a special paper session on beat induction at the ICMC 1994 to which several of the researchers mentioned above contributed.
In this broad study, which builds upon these contacts, we will aim at achieving a better understanding of the beat induction process by ordering and reformulating the different models and the subprocesses involved. Because there is such a large body of work upon which we can build here, we have designed the beat induction study around collaborative projects with the main contributors in this field. We will compare approaches first within, then between families, and address hitherto untouched aspects of beat induction modeling (recurrent syncopation, use of timing information). Finally, we will link them to empirical data, both existing and new. Before the projects will be described, we will describe how this experimental data is obtained.
Rule-based
Optimization
Search
Control and Complex Dynamics
Distributed
Minskian
Neural net
Statistical
Musicological
Table 2. Formalisms used in the modeling of beat-induction
(1) Evolution of the beat percept over time. For tracing the evolution of a beat percept over time, we will conduct an experiment in which subjects are presented initial fragments of different lengths of a pattern, i.e., using a gating paradigm. The proper task (e.g., tapping the beat, judging the goodness of fit of a presented probe beat, or detecting stimuli with contrasting attributes) will be decided upon on the basis of pilot studies. Assuming that a form of response can be found that reliably measures a beat percept, the responses will be grouped such that the evolution of that percept can be tracked over time. Two sets of stimuli will be used: the initial fragments of a set of national anthems and a combinatorially complete set of patterns. The analysis will give answers to the following general questions: how fast is initial beat induction, how much past information is used in updating the beat percept, how persistent is a formed beat percept, how does tempo influence beat induction, and is there a preference for beat durations and phases? The above questions can be answered globally without relying on a specific model. However, the different models predict much more detailed hypotheses about the process (e.g., the Longuet-Higgins & Lee (1982) model predicts that it takes between two and three beats worth of material to induce a beat). The use of the data of this experiment in the study of the different models is presented later.
(2) Synchronizing to the beat through tempo changes. In beat induction one has to track the tempo of the performer, which may vary widely. The human capability to synchronize with changes in tempo in isochronous patterns has been systematically studied by Michon (1967). More informal data on accompanists tracking tempo changes in real musical data is available from experiments done by Dannenberg (1993). This data will be complemented by our own more systematic experiments, that will collect the responses to step, impulse, ramp, and sinusoidal tempo changes artificially imposed on simple material. The onset of the tempo changes, and the induced beat will be experimentally manipulated, so as to be able to study the behavior of the tempo tracking process in-between, and on beats.
Furthermore, the tracking of the tempo in a final ritard (the typical slowing down at the end of a music performance) will be investigated. The ritard will be generated artificially on the basis of the models brought forward by the proponents of the physical motion analogy (see physical motion study). The possible dependency of tempo tracking on the rhythmic material will be investigated, using a musical theme and its rhythmic variations, as will be the limits of the temporal tracking capability for fast changes in tempo.
(3) Indication of expected beats in brain potentials. It is still under consideration whether to use the Event-Related Potential (ERP) facilities and expertise available at NICI to measure the brain's response to unexpected stimuli (like a syncopation) and use this as an alternative method to evaluate the psychological validity of the computational models. Because the expectancy-based theory of beat induction presented in (Desain, 1992a) directly predicts the amount of "surprise" for each new onset (or lack thereof) this seems an ideal theory to drive the design of ERP experiments on rhythm perception. ERP has the added advantage that responses can be extracted for every event in the stimulus - a gating approach is not needed. However, the method has been most successful for quite late (semantic) stages of processing, and although these effects already have been shown for harmonic expectancy (Bresson, Faïta & Requin, 1994; Cohen, Granot, Pratt & Barneah, 1993; Janata, 1995), the method still awaits a pilot study to show that the traces of the process of early rhythm perception can indeed be shown consistently in ERP's. Only then this line of investigation will be taken up.
Besides our own experiments, we will use existing empirical data and available musical score databases for the evaluation of the computational models of beat induction as well.
(4) Beat induced by cyclic patterns. Steady-state cyclic patterns are the only material for which computational models have been validated in systematic empirical studies (Povel & Essens, 1985; Parncutt, 1994). These experiments are most valuable, because several different tasks were used to measure the beat percept. There is no need to reproduce these experiments, but the findings will used in the validation of a whole set of models.
(5) Beat induced by isochronous patterns with loudness accents. These experiments will be realized in an anticipated project by Prof. E. Clarke at Sheffield University. Using a variant of a probe method developed by Krumhansl (e.g., Krumhansl, 1979), the influence of dynamics on meter induction is investigated. The results of these studies will be used to extend existing computational models such that they can deal with dynamics (see below "Dynamic aspects").
(6) Meter explained on the basis of regularities in musical scores. The use of databases of musical scores form another source of useful information. The temporal structure present in the score (e.g., time signature, note durations, rhythmic patterns) and other composed regularities are a useful source of information to test models of beat and meter induction, and have been used successfully in previous studies (see, e.g., Palmer & Krumhansl, 1990). More and larger databases of musical scores have become available lately (Hewlett & Selfridge-Field, 1995) that can be used for these analyses. We will focus on pieces previously used in the literature to make a comparison with other results possible. These data will mainly be used in the study with F. Lerdahl (see below "Musicological models"), although they can provide other models with a good first test as well (see Desain & Honing, 1995).
Below the five collaborative projects will be described, each of which concentrates on a specific family of beat induction models.
In their influential theory of grouping structure and meter Lerdahl & Jackendoff (1983) postulated three kinds of accent in music: phenomenal accent, structural accent and metrical accent. In their theory a number of rules is described that are concerned with meter. While there has been critique on the status of the theory as a formal model, the section on meter seems to be realizable in the form of a computational theory. A number of aspects, though, still have to be clarified, like the interaction between the different rules and their precise formal description. The result will be a computational model that will look at the material globally (not as a process model) and derive a meter. Lerdahl's idea (personal communication) that a priori likelihood of different meters are important will be explored as well. The model will be tested on a corpus of musical scores to assess its musicological validity. With Lerdahl the different design decisions in the formalization process will be made. The issue of how to formalize the importance of long notes for beat induction (which is realized in Longuet-Higgins & Lee's model, Povel's model, as well as in Lerdahl's work, albeit in completely different forms) will be clarified by experimenting with different rules and weightings within this musicological framework. The baseline against which these findings can be judged is the Palmer & Krumhansl (1990) frequency profile as mental representation of musical meter, which is completely event-based and ignores note-lengths. This study will use a database of musical scores, as described above.
The Longuet-Higgins & Lee (1982) rule-based model of initial beat induction still is a landmark in the literature. With Christopher Longuet-Higgins, we have collaborated on a new implementation of a model that can be considered a follow-up of the original (Longuet-Higgins, 1994). For this model the incremental, real time behavior has been elaborated more thoroughly. Lee also proposed an extended version (Lee, 1991), though at present the relationship between these different proposals is not clear. A formal analysis of the control structure of the three models has been made, as well as re-implementations (Desain & Honing, 1994c). With the new implementations and with the help of characteristic input sets (nested, combinatorially complete abstract sets derived from a formal grammar and a large corpus of composed rhythms) a statistical comparison between the models has been made to characterize their behavior (as an example, see Figure 2, which visualizes the amount of agreement of the models on the set of national anthems). This approach leads as well to an optimization of their parameters (Desain & Honing, 1995). These analyses were all made on the basis of functional equivalence between the model and the meter as notated in the score.
Figure 2. The amount of agreement of the models on the set of national anthems, depicted in a histogram. The x-axis indicates the duration of the pattern that is used as input to the model. The height of the bar shows the proportion of patterns of that duration for which at least two models agreed. The black part of each bar indicates the proportion of patterns for which all three models agreed on the beat.
We will proceed with a formal analysis of the rule-sets themselves and a derivation of assertions about the logical relationship between the input and the internal state of the model that remains invariant during computation.
In collaboration with Longuet-Higgins, we will try to interpret the results in terms of the formulation of the rules themselves. Second, we will formalize the different control structures used in these rule-based models (event-based, window-based, and time-unit based), and a proof of their semantic equivalence. Third, we will search for a good formal (grammar-like) characterization of a subset of regular rhythms (unique strict metrical patterns in some form) and the behavior of the models for them.
Because these models explain the formation of a beat percept as an incremental process, the psychological validity of the model can be affirmed by showing the resemblance of its behavior over time with the behavior of human subjects. There are a number of predictions that can be derived from the models. For instance, the fact that the beat percept always grows (the interval between beats becomes longer in the process), it takes between two and three beats worth of material to induce a beat (this can be related to the speed of beat induction), the beat is independent of global tempo (the absolute duration of the pattern has no influence on the output of the model), and relatively long notes cause the process to cancel the current beat percept. The gating experiment (experiment 1), described above, will provide empirical data to test these derived predictions of the models.
Furthermore, these models postulate a processing window of events spanning just one beat. By re-analyzing the data from the gating experiment (aggregating it to equal final fragments), it can be determined how much information in the history of the temporal pattern is still effecting a change in the beat percept. These predictions can be tested against alternatives, like a memory window of a fixed duration or a fixed number of events. (Note that, although this test is model-driven, it captures a global attribute, or constraint, of the beat induction process. The size of the window, and whether it depends on the present beat percept, can be determined regardless of the correctness of the rules that govern the evolution of the beat percept in time).
This study may link this -quite successful- rule based approach to beat induction, stemming from AI and Music theory, more closely to the psychological work on beat perception.
The model brought forward by Povel & Essens (1985) for cyclic patterns is another important contribution. It is distinguished by the empirical support with which it was presented. More recently, Parncutt (1994) presented an alternative model for cyclic patterns. This model has a different and more continuous formulation of level of accent and is dependent on global tempo. The relation of this model to Povel's one is unclear. Together with Povel, we propose to first refine his model to a continuous weighting of level of accent depending on global tempo, but keeping the logical structure of the accent-rule intact. Then we can postulate a more general model that subsumes Povel's and Parncutt's models. This will be subjected to the existing experimental data of both Povel's and Parncutt's work, and an optimal parameter setting will be sought. This will hopefully yield insight into the relative importance of the various components of both models. Finally, we proposes to proceed by elaborating these abstract models into a process model, or to transplant the accent rule, which forms the basis of the success of this work, to other models that already have a process character.
There is another family of models that concentrates on the problem how to track a (given) beat when the tempo changes (gradually, like in a tempo rubato, or suddenly, like in a tempo change). The system described in Dannenberg (Allen & Dannenberg, 1990) uses control theory, Large & Kolen (1994) take a more modern complex-dynamics approach of coupled non-linear oscillators, Longuet-Higgins (1976) musical parser tracks the tempo on each metric level, and the distributed model presented in (Desain & Honing, 1994a) can, because of its continuous nature inherently deal with tempo changes.
For this family of tempo-tracking models, first a formal analysis will be made of the different methods involved. This will give us a better insight into the differences and similarities between the formalisms used. From this analysis it might be possible to construct a generalized tempo-track method that can be used as an additional module to existing beat-induction models that cannot deal with tempo change in the input. In this way, we separate the different aspects of beat-induction, and allow different approaches to benefit from each other's strengths.
The psychological validity of the tempo tracking aspects of these models is hard to judge, the more so since they are presented as general models for beat-induction, not as specialized theories of tempo tracking. We propose to study the tempo tracking behavior in isolation, by either disabling parts of the models, clamping their internal state, or by presenting simple inputs, like sequence of notes with the same score duration. The response of these models to gradual and sudden tempo changes will be studied (see above, experiment 2). This data will be compared to results from Michon (1967) for human tempo tracking of simple sequences and data from Dannenberg (1993) on human accompanists for real musical data.
One of the issues is to determine in how far rhythmic material in between beats is essential in tempo tracking, since both Longuet-Higgins (1976) and Desain & Honing (1994a) depend on this information but the other models are essentially "deaf" to in-between beats. Because this issue has not been addressed in the literature, new experiments are foreseen with stimuli that have a carefully elaborated relationship between their metric structure and the tempo change.
Because most models of beat induction are restricted to patterns of onsets only, the role of intensity is rarely considered. Clarke recently submitted a proposal to the British ESRC to set up a study focusing on the importance and contribution of dynamics to the process of beat and meter induction. This proposal entails a number of empirical studies to investigate the role of intensity accents in isochronous patterns in situations of syncopation and metrical change. Our proposed contribution will be to look for ways in which the existing computational models can be opened up to deal with dynamic information. For example, non-deterministic extensions of rule-based models can make use of dynamic information by mapping it to the probability that a certain rule fires. In other models (e.g., Povel & Essens, 1985) intensity could be interpreted as a weighting of the events contributing to the amount of accentuation. We will extend the beat induction model presented in (Desain & Honing, 1994a) such that it can deal with intensity (as a weight on the individual onsets) as well. From the different predictions these theories will make, Clarke's stimuli can be designed more critically - contributing a more model-driven approach to his experimental work.
Like the study on dynamics mentioned before, we will investigate how attributes of music, other than rhythm alone, can influence the induction of beat or meter. In music theory these interactions are understood on the basis of melodic or harmonic accents (Dürr, Gerstenberg & Harvey, 1989, p. 810). The general assumption in describing the processes involved in the perception of harmony/melody on the one hand and rhythm on the other is that these are independent and the outcomes are combined at a later stage (see, Longuet-Higgins, 1976). Although melodic and harmonic structure can in itself convey beat or meter (e.g. when the rhythm is isochronous), most of the time these aspect are congruent with the rhythmic structure and the beat can be successfully determined on the basis of rhythm alone. However, harmonic and melodic cues can be very strong, especially when a form of coding or chunking (e.g., Deutsch, 1980; Deutsch & Feroe, 1981) is activated, e.g., when melodic fragments are repeated (Steedman, 1977). Van Egmonds work (Egmond & Butler, 1995), that describes all music theoretically possible melodic structures that can occur in the tonal system and their preferred mental representations, appear to be a good starting point to investigate the role of melody and harmony in the induction of meter. The study focuses on the question how existing models, based on rhythm alone, can be opened up to coding-models treating the other aspects (and not so much the elaboration of these models themselves). We will try to formalize this interaction staying close to the music theoretical notion of accent. The question whether indeed the processes of beat induction based on different factors can be modeled separately, and how their results are combined, will be investigated in a set of experiments with conflicting cues, using an information-integration analysis (Massaro & Friedman, 1990).
Dynamic attention theory for temporal patterns has always stayed on the brink of formalization (Jones & Boltz, 1989). It seems that expectancy-based models of rhythm perception (Desain, 1992a) can make the construct of dynamically unfolding attention much clearer. A crucial aspect here is that events are processed depending on the level to which they were expected. This expectancy is generated by past events and projected into the future. With Jones, the relationship between expectancy and attention will be explored. The empirical data regarding the evolving beat-percept gathered in the gating experiment will be reinterpreted in the light of this theory. This work will aim at a clarification of the theoretical constructs and at an elaboration of the relationship between expectancy and attention and their concrete formalization in a computational model.
Next to these collaborative projects, advanced issues of beat-induction modeling which have been introduced in (Desain & Honing, 1994a) will be evaluated more systematically. We mention here the treatment of recurrent syncopation, the adaptation to changes of meter and the use of expressive timing information itself for the beat-induction process.
Wherever possible, abstractions and generalizations from the different models will be made. The project is aimed at finally collecting all papers from the collaborations above in one publication, together with simple implementations of all models, e.g. for use in courses on music cognition. Thus we hope to further this complex field of research by presenting an overview and taxonomy of the work done, connecting the different research efforts, making the computational models more accessible, linking theory and experimental data more thoroughly and addressing some hitherto untreated aspects.
A grace note is a musical ornament, that is, a short note played just before a main one. It falls within the broad music-theoretic category of ornaments to which, for example, trills belong as well. In the musical score the duration of these notes is not indicated, their actual length is left to convention and the performer. They are not part of the metrical hierarchy, they are overlaid on the rhythmical structure, as one would expect of an ornament. There are different types of grace notes, depending on their musical context, the most important classes are appogiatura, so-called time-taking ornaments and acciaccatura, timeless ornaments (Ward, 1977; Neumann, 1986).
Figure 3. Grace notes for three repeated performances in three tempi. The interonset interval stays invariant from the medium to the fast tempo, but seems to scale proportional from the medium to the slow tempo. (White marks indicate measured interonsets, black marks indicate averages, the line indicates predicted interonsets in case of proportional scaling; Adapted from Desain & Honing, 1994b)
It was recently discovered (Desain & Honing, 1994b) that these music theoretical distinctions are revealed in performance. While different types of grace notes may be played with the same duration in one performance, they behave differently when the performer is asked to play at another overall tempo. While some grace notes scale their duration proportionally with the global tempo, grace notes of another type retain a fairly constant duration across different tempi, and for still others the scaling behavior obeys a more complex regularity (see Figure 3). For these grace notes there seems to be a change in the nature of timing around a certain rate. We believe that this finding is related to the findings in time perception experiments (e.g., van Noorden, 1975) that show a same abrupt change.
To further our understanding of these phenomena we propose to investigate the dependency of grace note timing on global tempo using pieces of music for which thorough music theoretical analyses exist. To allow a more systematic investigation of these dependencies, as we will do in experiment 1, a fine scale of tempi and a larger number of repeated measurements will be used. Next to the interonset-time between grace note and the next note, the difference between the onset of the next note and its estimated onset time (based on the note before and after it) will be measured as a dependent variable as well. This is done to find evidence for the observation that the timing is controlled, depending on the type of grace note, such that the "beat" falls either in between the grace note and the note or on the main note.
Although this research will provide descriptions of the phenomena, it will not help us propose candidates for an underlying mental representation. For this, we have to turn to a research method pioneered by Wing & Kristofferson (1973) and elaborated further by, among others, Vorberg (1992). They propose a model of mental time keepers whose structure can be revealed by the analysis of the stochastic nature of the timing jitter. We will turn to this technique of analyzing the covariance of the successive time intervals between note onsets in replicated performances at the same tempo, instead of the gross differences in tempo that constituted the independent variable in the previous experiment. In experiment 2 we will collect massive replications of the grace note performances in order to be able to conduct the covariance analysis reliably. This method will then permit us to test different linear and hierarchical structures of mental timekeepers that control the initiation of the onset of the grace note and the next note (see Figure 4). It allows as well to factor out the influence of motor noise. We will explore the potential of this method, originally developed for the analysis of simple tapping and synchronization tasks, for use with more musical material. We expect to find the same distinctions between different types of grace notes, and hopefully even find an underpinning for intuitive musician's notions like `playing towards ...' or `stealing time from ...'. With Prof. D. Vorberg we will investigate whether the notion of mental timekeepers can be extended towards a more planning-like construct, in which an anticipated future onset can be used to control the timing of an ornament that has to happen before it.
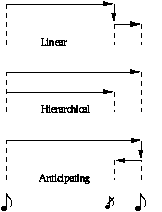
Figure 4. Hypothetical mental control structures for the performance timing of a grace note.
In (ten Hoopen, Hilkhuysen, Vis, Nakajima, Yamauchi & Sasaki, 1992; Nakajima, ten Hoopen & Van der Wilk, 1991) it was shown how the perceived duration of a temporal interval is affected when a short interval is presented just before it. Although this finding from psycho-acoustics has been known for some time now, it is still common practice to simply remove grace notes from performance data to study, for instance, the rubato structure. A simple listening test reveals that when grace notes are removed the temporal flow is disrupted remarkably. Thus, the findings of ten Hoopen and his colleagues for empty time-intervals may apply as well to truly musical material. This hypothesis will be tested in experiment 3 in which music is performed with and without grace notes. The dependent variables, both the duration and the onset of the main note, will be related to the presence or absence of the grace note before it, and its type. In specific, we will test a model developed by Nakajima (personal communication), which attempts to explain how neighboring time intervals interact in perception. A perceptual experiment will test if the temporal flow in performances where grace notes are artificially removed can be corrected by this model, over a range of tempi and for different types of grace notes.
Given the fact that the independently modeled aspects of grace note timing are in computational form, they can be combined. This may even entail a reduction in complexity, because the scaling behavior initially explained on the basis of the type of grace note may now be attributed to an underlying structure of timekeepers. An object-oriented design methodology can help in exploring perceptually and musically relevant taxonomies of ornaments (Desain & Honing, 1993). This should, we hope, yield a sparse and elegant taxonomy of types of graces notes and transformations thereof. This taxonomy should elucidate the complex patterns of behavior found in performance and help factor out the knowledge shared on different levels of description. Such a taxonomy, developed within the context of computer science, should be subsequently reinterpreted by a musicologist, who can contribute music-theoretic knowledge about distinct grace note types. This will complete the computational modeling of grace note timing based on type. How these types can be derived from the melodic and harmonic context of the music is, of course, another question.
A timing model for ornaments will be the right basis for a data representation in technological applications (e.g., a MIDI sequencer) that allows for perceptually plausible editing operations (like insertion or deletion of these ornaments). Furthermore, it will help with applications where the tempo of a performer is tracked by computer, as well as applications where decisions of the categorical note durations must be made (e.g., music transcription).
This study proposes to separate the expressive signal into its structural elements based on a generalization of existing generative models (e.g., Clynes, 1987; Sundberg et al., 1989; Todd, 1989). It will shed more light on the anatomy of expressive timing and dynamics, and will yield ways to estimate optimal parameter settings for the models and estimations of the amounts of variation that can be attributed to the different musical structural descriptions.
Expression is defined in this study as a syntactic concept: the pattern of deviations of attributes of performed notes from their values notated in the score (see Figure 5 for an example of such a signal). The interpretation of the score by the performer, all deviation from a strict mechanical performance, is named expression. A better definition is not necessary in the context of this study. The form of expressive deviations has been the topic of many studies, starting from exploratory ones (Seashore, 1938; Povel, 1977), to detailed proposals stating that expression is only based on -and intended to communicate- musical structure (Clarke, 1987, 1988). This hypothesis, that expression is based directly on musical structure, will be central to the proposed research.
Figure 5. Timing patterns of eight bars of a Beethoven Theme (three repeated performances).
The concept of musical structure is not a simple one because of the multitude of common structural descriptions. We will assume that music-theoretic structural descriptions (like melodic and harmonic structure) can only influence expression via the induction of a temporal structure that hierarchically subdivides time (like meter, rhythmic grouping and phrase structure). The structural relation considered here is restricted to a part-of relation. The different hierarchical structural descriptions are concerned with different aspects of a piece, and may be incompatible. They may violate each other's boundaries - for instance a phrase ending in the middle of a measure. Ambiguity may arise when there are several mutually exclusive analyses possible of the same aspect of a piece. And there may be a local violation of otherwise hierarchical structure, like overlapping phrases. In this project we will always assume that the structural descriptions are known, either from the score, from music-theoretic analyses or by interviewing the performer.
The work is based on computational theories that generate a performance from a score and a structural description. The three main generative theories that will be used are Clynes' composers' pulse based on metric structure, Todd's parabolas linked to phrase structure, and Sundberg's rule-system for local features.
Clynes (1983; 1987) proposes composer-specific and meter-specific, composer's pulse (not to be confused with his more controversial sentic forms): a recursive uneven subdivision of the time intervals representing the structural levels (e.g., in the Beethoven 6/8 pulse the subsequent half-bars span 49 and 51% of the bar duration and each half bar is divided again in 35, 29 and 36%). This composer's pulse is assumed to communicate the individual composer's personality. A similar procedure is given for dynamics. This generative theory stems from intuition, but the artificially generated performances indeed capture important regularities in performance as is shown in evaluation studies where subjects compared real and artificial performances (Clynes, in press; Repp, 1990). And in other studies it is confirmed that meter is indeed communicated somehow to the listener by means of expressive timing (Sloboda, 1983)
Todd (1985; 1989) postulates parabola-shaped tempo curves linked to the phrase structure that hierarchically add up to yield the final tempo profile. A more general picture of this line of research can be found in (Shaffer, Clarke & Todd, 1985). The nonuniformity of the phrase-structure (phrases at the same level do not necessarily have the same length) is treated by stretching the parabolas. The dynamic (loudness) contours are proposed by Todd to have similar structure - but in contrast with Clynes even the same parameters are used for dynamics - leaving one final tempo to loudness mapping (Todd, 1992). The parameters for his model were derived by a fit to empirical data by eye.
Sundberg et al. (1983; 1989) propose a rule-based system to generate expression from a score based on the surface structure. Each rule in this system looks for a specific local pattern (e.g., a large pitch-leap) and modifies the timing (in this case, inserts a small pause). Rules and parameters were derived in an analysis-by-synthesis paradigm with one expert changing the rules and listening to the results. Later confirmation of the working of the rules was sought in evaluation studies in which listening panels had to rate artificial performances. Van Oosten (1993), has undertaken a re-implementation and a critical evaluation of this system.
It is disturbing that in the literature no generative models, nor systematic studies, are found on the relationship between rhythmic or figural structure, and expressive timing, even though this source seem to account for a large proportion of the variance in the expressive signal (Drake & Palmer, 1993). Only Johnson (1991) presents a model that directly links rhythmic patterns (series of score durations) to expressive profiles - but this rather technical study did not have a follow-up.
It is remarkable that the methodology of directly fitting the model's output to the empirical data was never pursued. The models were tested fragmentarily, if at all, by an analysis-by-synthesis paradigm, by perceptual experiments, or simply by visual comparison of the output of the model with a real performance. All three generative models contain parameters, which can be given appropriate values by fitting the model to measured data. A possible reason for the reluctance to use this simple device is that each model only explains the contribution of one kind of musical structure to the expressive profile (be it metrical, phrase or surface structure). As such, the process of optimizing the parameters to fit the data is confounded by the many components that are contributed by the other types of structure. For example, a large tempo deviation, like a final ritard, establishes such a large trend in the data that fitting a regular repetitive profile linked to metrical structure becomes impossible. This means that promising models cannot be tested directly and that the role of musical structure and the important hypothesis that musical expression is directly based on it cannot be evaluated further.
A good solution to this problem can be obtained by fitting the performance data at once to the combined outputs of all models - optimizing the parameter settings for all models at the same time (see Figure 5). The prerequisites for this approach is A) that appropriate rules of combination of the contributions of the individual models can be formalized, B) the models form a more or less complete set that can in principle explain most of the variance in expressive timing (no structure is overlooked) C) the way in which each model calculates the expressive component is more or less valid, D) proper optimization methods exist for fitting the outcome of the combined models to the data and E) an error measure can be defined for expressing the difference between generated and real performance.
Figure 5. Fitting the combined timing profile to empirical data .
Regarding aspect A, the rule of combination, we might take the success of multiplicatively combining tempo-factors (as is done for different levels of the metrical hierarchy in Clynes' model, for different levels of the phrase structure in Todd's model) as an indication that this has a general applicability (there is more evidence for that; see, e.g., Repp, 1994). However, the combination has to allow additive combinations of, for example, inserted micro-pauses as is done in Sundberg's model as well.
Regarding aspect B, the completeness of the set of models, the most obvious problem is that there is no complete model available to explain expression based on rhythmic structure, the more so because there is evidence that this factor may be responsible for a large proportion of the timing variance (Drake and Palmer, 1993). The elaboration of such a generative model along the lines of Johnson (1991) seems the best approach, and will form part of this study. The final ritard may be another aspect that needs a separate modeling effort.
Regarding aspect C, the validity of the expressive shapes resulting from the models, we will reformulate the models to yield a more general, more abstract description of the expressive gestures, before trying to fit them to the data. Of course, this generalization may not introduce too many new parameters.
Regarding aspect D, the optimization method, the problem may well be ill-structured (i.e. exhibit many local optima) and a method that is rather insensitive to this, like simulated annealing, needs to be used. The size of the optimization problem (ten to thirty parameters, hundreds of values to fit), although requiring a fast computer, falls within the range of the possibilities with present technology.
Regarding aspect E, the RMS-deviation of onset times can be used as a simple physical error measure. However, because not all deviations will be as important perceptually, a good measure would have to be based on models of accuracy of timing and tempo discrimination (ten Hoopen et al. 1994) - a psycho-physical measure for temporal patterns. But it will be difficult not to end up in a circularity where the separation contributes a large proportion of the variance to one model because the error measure disfavors certain types of errors.
Research in expression can make a major step forward when the proposed method succeeds. Only then can an empirical basis for the individual generative models emerge. The results will make it possible to estimate their validity and relative importance based on the amounts of variance that is explained by the respective models. Furthermore, the results will effectively establish a more general model that subsumes the known ones and formalize their coherence.
Given a successful fit of performance data, the expressive signal can be effectively decomposed into its separate components and can be manipulated in musically plausible ways (e.g., an exaggeration of only the rubato linked to the phrase structure). This type of transformation was already available in the calculus for expression (Desain & Honing, 1991b), but because a separation of expression into its components was not available, only one structural description could be used at a time and transformations to interacting types of expression could not be handled. Apart from applications in the music studio, this new method will allow the construction of stimuli in which the expression of a musically sensible fragment of music is manipulated. Most psychological research in music performance use global measurement methods (e.g., average performance data and correlation measures of timing profiles of whole pieces). Recently, though there is a tendency to take a more structural approach (cf. Repp's latest work) - the separation technique will allow the experimental design to focus on one structural aspect, while still using relatively rich musical fragments.
When the method is proven to work well, the decomposition of expression yields a good and economical encoding. For example, instead of individual tempo measurements per note, one now only has to store a set of parameters for a systematic tempo profile that will be repeated per measure, plus parameters for the phrase-level rubato, and so on. This economy of encoding, when successful, can be interpreted as evidence for the mental representations of that specific structural aspect. The alternative mental representations can be investigated directly by redoing the decomposition analysis using different structural descriptions, like incompatible phrase-structures, different levels of a metric hierarchy, different spans of figural coding, etc. The descriptions that yield the best decomposition of the expressive signal, explaining most of the variance, can be argued to be the best candidates for the mental representations active during the performance. Thus, light can be shed on questions that remain unsolvable in musicology itself, like how many levels of the metrical hierarchy upto hyper-meter are actually activated and exhibit themselves in the performance of skilled pianists. This extends the technique from attributing expression to different known structural sources, towards the inference of structure itself directly from the expressive signal. It will be computationally tractable only when a limited set of possibilities for structural descriptions can be pre-selected on the basis of some criterion, but even then it is a promising direction.
Depending on the success of the research, it might be possible to explore voice asynchrony and articulation as extensions of the models, to investigate the interaction between timing and dynamics (a complex problem) and to address parameter changes over time as well, but these issues will be ignored during the first and main stages of the work.
The empirical parts of this study will at first consist of the collection of performances under different conditions. We will restrict ourselves to piano music, but address different musical styles (i.e. classical, jazz, etc.) because structural descriptions and ways of using expression differs so much across styles. Professional pianists will be used as subjects. They will be instructed to play the same piece under different conditions, for example, with alternative meter and phrase markings in the score. Repeated measurements are needed to obtain estimates of the levels of unintended (motor) noise in the performances. Optimizing the explanatory power (minimizing the error) of the combined model for these performances can then be undertaken.
A second experiment will test how the results of the combined model of expression is evaluated by a listening panel, and whether they can still be distinguished from real performances.
The models are already available in POCO (Honing, 1990), a workbench for research on musical expression, but their implementation will have to be adapted and generalized for this project. POCO also has the tools needed for collecting performances, creating and annotating scores, matching scores and performances etc. Data collection needs to take place on a good MIDI grant piano. There are contacts with the Den Haag Conservatory (P. Berg), Sheffield University (E. Clarke) and Ohio State university (C. Palmer) (in order of the quality of the equipment) where these recordings can be made. Some simple (non-systematic) material is readily available which will make a quick start of the project possible.
Most of the research in the psychology of music dealing with expression is concerned with the discrete aspects of music performance, and mainly concentrates on the study of piano music. In these studies only the time of attack of individual notes (and possibly the release time) is studied as carrier of musical expression. However, on other instruments, what happens during and in-between notes can be more relevant then the realization of the note onsets and offsets themselves (Strawn, 1989), an issue not often addressed in music psychology. A noteworthy exception is the work of Seashore (1967) who pointed out the importance of the continuous aspects in music performance. He and his colleagues studied, for instance, the use of vibrato in violin playing and of portamento in singing. The musical parameters were analyzed through so-called "performance scores" in which, next to the conventional music notation, pitch and dynamic contours where notated (extracted from sonograms). It was shown that musicians achieve a high level of control and systematic consistency over the fine details of pitch and amplitude contours in their performances. Large perceptual differences in how, e.g., a particular vibrato ends at a certain phase and moves into a glide from one note to another (see Figure 6), indicate that this type of control is essential in music performance.
It is remarkable that, since these early exploratory studies, this field received little attention (exceptions are, for instance, Clynes' (1987) informal observations that there are systematic regularities in performed vibrato that are composer-specific). A reason for this could be the relative inaccessibility for psychologists and musicologists of the data processing techniques needed. Especially from the domain of signal processing and computer music, several synthesis and analysis methods are available now that can support the study of these meaningful modulations in music performance. Recent techniques that combine Short Time Fourier transforms with "intelligent" peak-tracking (Quatieri & McAulay, 1985; Serra, 1989) can form a solid basis for the analysis, modeling and synthesis of these modulation signals. Another reason for the neglect of this field may be the amount of information present in these modulation signals. Compared to discrete data there are many more degrees of freedom to explain. And finally, direct experimentation without a model is not likely to give results that go beyond the exploratory studies of Seashore and his colleagues.
Figure 6. Types of Portamento used in singing (from Seashore, 1967, p. 272).
However, while the availability of current signal processing techniques makes the modulation signals (of pitch or dynamics) easier to extract, their shape is still quite complex. It is difficult to analyze and model them directly. We propose to first decompose these measured modulation signals into idealized components, whose behavior under different temporal conditions can then be studied separately.
As a concrete example, consider measured transitions between two notes with a vibrato, like those depicted in Figure 6. From visually inspecting these curves, the hypothesis may arise that such a transition (Figure 7a) can be decomposed into an additive combination of a periodic signal (the vibrato; see Figure 7b) with a certain development over time (frequency and depth), and a monotonic transition function (e.g., a sigmoid; see Figure 7c) which describes the path from the pitch from the first to the second note. In turn, the vibrato (Figure 7b) can be modeled as a sine wave, parametrized with a decreasing linear ramp for its frequency (Figure 7d) and a decreasing amplitude (Figure 7e).
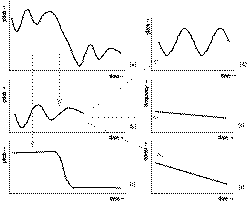
Figure 7. Decomposition of a transition between two notes.
This proposed decomposition can be formalized and verified using a workbench that is designed for the construction of control functions for sound synthesis (Desain & Honing, in press). It facilitates the composition of abstract control functions based on a formalism named GTF (Desain & Honing, 1992c, 1993d; Honing, 1995). The user can build a mathematical model of the proposed decomposition aided by the availability of a library of basic functions and standard ways of combining them and by a graphical and aural user-interface for evaluating the preliminary results. The workbench can estimate the best parameter settings for the function, optimizing the fit between synthesized and measured data using simulated annealing (Otten & van Ginneken, 1989). In this way a reasonable algorithmic description of individual note transitions can be obtained.
To move away from an idiosyncratic formal model of one specific transition, the workbench supports model fitting to multiple instances at once, be they repeated performances of the same transition, repeated occurrences of the same musical material, or even transitions in which, for example, the duration of the notes differ. The basic functions in GTF have access to multiple notions of time (start-time, duration and absolute time) makes it possible to express abstract temporal behavior non-procedurally. By temporal behavior we mean here how a function changes when it is applied to, for instance, a longer or a later time interval. For example, a vibrato adds more cycles when applied to a longer duration, while a glissando stretches elastically when allowed to take more time. Thus one abstract function might be constructed that models the behavior of a class of transitions. This allows the definition of a much more general description of the phenomenon and brings out the regularities observed by all instances.
Of course, the generality of the thus-constructed description depends on the availability of data from different conditions. For example, when the ending of a vibrato can be studied for notes of different durations, and in different contexts of subsequent material, a constraint on the ending of the vibrato function may be found (e.g., always complete a vibrato cycle before moving to the next note) and when studying transitions over different pitch intervals a regularity observed by Clynes (1987) may be found (i.e., the point of deepest vibrato is dependent on the direction of the subsequent pitch-leap). These regularities can be much more easily assessed with our model-driven approach.
Next, it should be remarked that the models will be instrument-specific and style-specific, and a proper choice of the domain is important. We will use classical violin and Japanese Shakuhachi performance as case studies. In the case of the latter instrument, continuous modulations are the main carrier of expression and an elaborated notation system and taxonomy for these modulations exists (see e.g., Fritsch, 1979; Gutzwiller, 1983). In the former, these aspects are not made explicit in the score, but a consistent performance practice exists. For both instruments good synthesis models (e.g., Smith, 1992) and good controllers for recording performances directly (eliminating the need for an elaborate analysis and re-synthesis of the audio signal) are either commercially available or available through contacts with colleagues (Prof. Chafe, CCRMA, Stanford, for violin and Dr. Katayose, LIST, Osaka, for Shakuhachi).
Without the proper perceptual underpinning, a performance modeling effort is much less valuable. In perceptual studies the human sensitivity for these kinds of modulations can be established, which will yield lower bounds for the model accuracy that needs to be achieved. But, more importantly, the question whether the regularities found in performance will be distinguished perceptually, recognized, and give rise to different judgments of musical quality, needs to be answered. For that we will use listening panels to judge the manipulated, re-synthesized performances.
In summary, this study on continuous modulation in music performance can build upon a formalism for expressing complex control functions and a preliminary version of the workbench for construction of these algorithmic models. The work entails the elaboration of the workbench, the collection of a body of transitions in violin and Shakuhachi performances within specific styles, the construction of algorithmic models describing these transitions, and the generalization to models describing families of transitions. In addition, hypotheses on these regularities will be tested, as well as their perceptual and musical relevance.
When a good model for specific transitions on a certain instrument and playing style is achieved, it forms in itself a contribution to our understanding of these continuous aspects in music performances. However, one should not lose sight of the more distant goal of understanding the role these modulations have in conveying the larger time spans of musical structure to the listener. It is hoped that this study may lay the groundwork upon which research can be based that narrows the gap of knowledge about continuous and discrete aspects of music performance. This gap was caused by the headstart gained by research of keyboard music, simply because of the ease with which piano music can be reduced to discrete note events.
Just as fundamental perceptual research on auditory masking made it possible for Philips to develop an effective data reduction scheme for use in digital recording devices, our work in models for higher levels of music cognition can sometimes be applied directly to relevant industrial areas. These include the recording industry, producers of electronic musical instruments, developers of music software for professional and home use, the so-called edutainment/infotainment business, and producers of interactive multi-media systems. In these areas there is a range of products which can benefit from good models of music cognition.
Besides the industrial affiliates program, which will stimulate the communication between the team and the industry in general, we seek to collaborate intensively on the development of a number of such products. These applications will be developed and financed from outside the Pionier project. The developers, though, will function within the Pionier team and benefit from the internationally unique combination of expertise in computer science, musicology and psychology and from the available facilities. We will apply for funds to the Stichting Technische Wetenschappen (STW) and other programs that support technology transfer between research and industry (e.g., ESPRIT). As examples we will present three applications in more detail.
Nowadays, the process of music editing still uses the digital equivalent of the old tape-splicing techniques. There is quite a gap between the level at which musicians and the recording team communicate and the kind of operations that are supported by modern digital audio equipment. In particularly, operations involving the musical structure and expression are not supported. By expression, we refer to the intended and meaningful deviations in timing and dynamics in music performance, aspects that make one performance so much more interesting than the other (Clarke, 1988). Requests like "bring out these phrases a little more by a deeper rubato" or "don't let the metrical structure become too obvious in the dynamic contour," cannot be readily translated into editing operations. Consequently, this results in many takes of the same performance. Current multi-track recording techniques and digital audio software treat expression, tempo, timing and synchronization as technical problems instead of an integral quality of performed music.
However, given richer and more structured (knowledge) representations of music (Desain & Honing, 1993c) than the ones in use today (i.e., audio signals and MIDI), musical performance expression can be brought under the control of the recording team. This is the key idea of the Expresso system (Desain & Honing 1991b; Honing, 1992): to facilitate editing operations that are meaningful at a musical level, with perceptually sound results. It is based on a calculus of expression that was designed to formally describe how different types of expression (onset timing, offset timing, dynamics, asynchrony) are linked to different types of musical structure (phrase, metrical, chord, voice, and surface structure), and how they can be manipulated while maintaining consistency. For instance, it will be possible to emphasize the expressive timing in a piano performance that communicates the phrase structure to the listener by means of rubato, and to modify the subtle, almost timbral, asynchrony between a leading melody voice and the accompaniment (see Rasch, 1979). Likewise, it will be possible to synchronize two individual parts of an ensemble piece, to remove a grace note, all of this such that the context, and the other aspects of musical expression, remain perceptually (but not physically) invariant. This is where we believe we can make an important contribution in the design of the next generation of hard- and software for recording studios. We are contacting the audio and recording industry to collaborate in the development and elaboration of these theories and prototypes, and to test their usability and applicability in music technology products. There is considerable demand in the recording industry for applications that reduce recording time (presently a new recording session is the only solution, even for small changes). There are initial contacts with Philips and PolyGram/Deca to see whether they can contribute in funding to the development of applications in this domain. This might lead to a collaborative STW proposal.
A dictionary is a well-known and often used tool. It constitutes not only an ordered list of words, but each item is annotated with its pronunciation, meaning, cross-references to synonyms and antonyms, declinations, etc. In music research and in composition the idea of a lexicon is not so widespread, except maybe for the Barlow and Morgenstern (1975) lexicon. In this dictionary a collection of classical themes are listed in such a way that a specific one can be looked up easily. Indeed the success of any lexicon depends on the ease with which information can be indexed and searched and the kind of help it offers in the search process. For example, because a melodic variation is not a concept that is easy to formalize, the search for a theme played with a slight variation will fail, even though the original exists in the lexicon.
In rhythm perception research, a number of theories have been developed that characterize certain aspects of rhythmical patterns like induced beat, amount of metricality, perceived tension or syncopation, similarity, perceptual beginning of a cyclic pattern, etc. (e.g. Barlow, 1987; Gabrielsson, 1974; Garner, 1974; Desain & Honing, 1994; Desain, 1992; Longuet-Higgins & Lee, 1982; Povel & Essens, 1985). This makes it feasible to design a database, a lexicon, of all possible rhythms, together with ways to navigate and search through the rhythm-space. Such a lexicon will contain a combinatorially complete rhythm-space, i.e. all possible rhythmical patterns, only limited by the length of the rhythmical pattern.
The way we envision the use of such a system is that a composer, musicologist or music student, enters a rhythm by playing it into the computer. The performed time intervals are quantized (Desain & Honing, 1989b) and a score of the performed pattern is displayed in common music notation. Whenever the pattern is recognized as a familiar pattern (say a samba, or a fragment from Stravinsky's "Firebird"), its name and some (ethno)-musicological data is shown, more information about composer, instruments and culture is available through hypertext links. Searches can be done in a number of ways. To give a few examples: "find a similar pattern with a stronger sense of beat", "find a similar rhythm that maximizes the sense of syncopation in this position", and "find a perceptually smooth transition path (an interpolation) from this pattern to that" or "what is the most exciting way in which I can distribute this rhythm over two instruments". Of course, the responses to these queries can be presented both aurally and visually.
We propose to develop this idea further, to explore its possibility and potential. Apart from the database technology, the largest amount of work is foreseen in the design of appropriate user interfaces and the concrete implementation of the underlying theoretical parts.
When it proves possible to access other databases of musical information (like the database from the Center for Computer Assisted Research in the Humanities, Stanford), to extract data about known rhythmical fragments, this will of course be preferred above hand-annotation of patterns.
During the development of the system, a network implementation (WWW) will be constructed that can be accessed worldwide. As such, the designers can benefit from users in studying their use of the system and eliciting comments. Part of the database will be open for users to add their own information (patterns, references, musicological description, links, etc.). A period of testing the system on the net will give a good indication of the features used most often, shortcomings and strengths of the system, besides pre-marketing the idea. After that, a final version will be constructed for CD-rom or CD-i.
In the future this project may be embedded in a larger one that deals with the search for imprecise matches of full melodic material. But the rules for perceptual melodic and harmonic similarity are so different from their rhythmic counterpart, that the restriction to rhythm seems wise. We foresee the need for other restrictions as well: timbral information will not be used, nor will dynamics, articulation and expressive timing. This makes a simple data-representation in the form of bit-strings possible (Dauer, 1988). Of course, a known rhythmic fragment might very well be annotated with a (MIDI or sound) file with all the proper instruments, dynamics and timing of a performance and possibly even a short video.
This project will be submitted to STW. Contacts with users that might be willing to support development (Philips, Buma-Stemra, Publishers) are in their initial phases.
In research on expression quite complex data processing is required, like matching, filtering and tabulation before, e.g., statistical analyses can be made. Complex processing is needed for the generation of musical stimuli and for tests of computational models. The development of idiosyncratic software for each project is a wasteful approach, especially since the data representation issues involved are quite intricate and the various existing formats are not trivial to implement.
POCO (Honing, 1990; Desain & Honing, 1992) is an evolving environment for the analysis of musical performances, especially with regard to expressive timing. It was initially developed at the Music Department, City University, London in a project funded by the ESRC. It is now further developed at the University of Amsterdam and the University of Nijmegen. A preliminary version of POCO has been made available on Internet and is currently being used by a number of researchers in music performance expression and music theory.
POCO has a consistent I/O model for musical information in different formats on different media. A general representation of musical structure (metric, phrase, voices, chords, etc.) in the form of part-of relations enables many operations and manipulations on musical data to be expressed easily. It has support for program development and system maintenance, and enables the programmer who extends the system to ignore details about the multi-modal user interface and the documentation, since these are generated automatically.
In this project we want to improve the main functionality of the system, such that a larger community of researchers and music students can benefit from the tools provided. Over the years, feedback from users, and our own experience in using the system, point at a number of weaknesses and shortcomings in the environment that need to be improved. We want to concentrate on the following projects: i) the development of a better pattern matcher that matches a musical performance with a structurally annotated score, ii) redesign of the automated user interface generation to deliver control panels for commands directly from the types of their arguments, iii) integrating the Calculus for expression (Desain & Honing, 1992b) into this environment, iv) development of a (graphical) structure annotation tool, v) development and documentation of extensions, programmers interface, and programmers documentation, vi) redesign and implementation of the POCO MIDI-file and I/O system, and, finally, vii) elaborating the support for version management, patch management, and user administration.
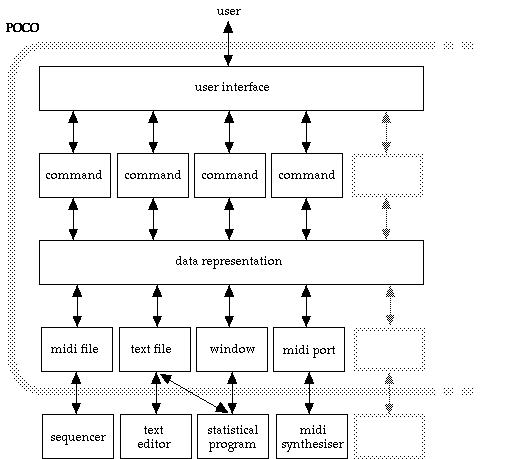
Figure 8. The architecture of the POCO system.
We will organize a three-day POCO workshop when a first round of these improvements is accomplished. The first day will be an introduction for first-time users. This could be staff and students from areas like music cognition, music theory and perception. The second day will aim at researchers in the field of music performance expression, who already use POCO or are considering using it in the setup and analyses of their experiments (e.g., research groups from Sheffield University, the Ohio state University, Haskins laboratories, Université René Descartes, and Northwestern University), to give them a fuller understanding of the facilities and to discuss future improvements. A third day will aim at researchers and programmers who want to extend the environment, and therefore need further insight into the inner data structures and programs (e.g., research groups from the University of Sheffield, Keele University, and the Institute de Recherche et Coordination de Acoustique et Musique).
POCO will be freely distributed for use at universities and conservatories. Most of the models and methods developed in this Pionier project will be integrated in the POCO environment, except tools dealing with continuous modulations. The projects will be realized by a Lisp programmer, assisted by a number of graduate students.
Abelson, H. and G. Sussman (1985) Structure and Interpretation of Computer Programs. Cambridge, Massachusetts: MIT Press.
Allen, P. & R. Dannenberg (1990) Tracking musical beats in real time. Proceedings of the 1990 ICMC, 140-143.
Anderson, J.R. (1983) The Architecture of Cognition. Cambridge, MA: Harvard University Press.
Balaban, M. (1989) Music Structures: A Temporal-Hierarchical Representation for Music. Musikometrika, Vol. 2.
Balaban, M., Ebcioglu, K . & O. Laske (eds.) (1992) Understanding Music with AI: Perspectives on Music Cognition. Cambridge, Mass.: MIT Press.
Barendregt, H. P. (1981) The Lambda Calculus: Its Syntax and Semantics. Amsterdam: North-Holland.
Barlow, C. (1987) Two essays on theory. Computer Music Journal. (11)1, 44-60.
Barlow, H., and S. Morgenstern (1975) A dictionary of musical themes. New York : Crown Publishers.
Bharucha, J. J. (1991). Pitch, Harmony, and Neural Nets: A Psychological Perspective. In P.M. Todd and D. G. Loy (eds.), Music and Connectionism. Cambridge: MIT Press.
Bowen, J.P. & M.G. Hinchey (1995) Seven More Myths of Formal Methods. IEEE Software, July 1995, 34-41.
Brachman, R. J. & Smith, B. C. (1980) Special issues on knowledge representation. SIGART Newsletter, 70:103-104.
Bregman, A. (1990) Auditory Scene Analysis: the Perceptual Organisation of Sound. Cambridge, Mass: Bradford Books.
Bresson, M., F. Faïta & J. Requin (1994) Brain Waves Associated with Musical Incongruities Differ for Musicians and Non-musicians. Neuroscience Letters 168. 1010-105.
Brown, J.C. (1993) Determination of meter of musical scores by autocorrelation. J. Acoust. Soc. Am., 94(4), 1953-1957.
Butler, D. (1992) The musician's guide to perception and cognition. New York: Schirmer.
Cardelli ,L. and P. Wegner (1985) On Understanding Types, Data Abstraction, and Polymorphism. ACMS, 17(4), 471-522.
Chafe, C. (1989) Simulating performance on a bowed instrument. In M. Mathews & J. Pierce (eds.) Current Directions in Computer Music Research. Cambridge, MIT Press. 185-198.
Clarke, E.F. (1987) Levels of structure in the organisation of musical time. In "Music and psychology: a mutual regard", edited by S. McAdams. Contemporary Music Review, 2(1).
Clarke, E.F. (1988) Generative principles in music performance. In Generative processes in music. The psychology of performance, improvisation and composition, edited by J. A. Sloboda. Oxford: Science Publications.
Clarke, E.F. (1993) Generativity, Mimesis and the Human Body in Music Performance. In Music and the Cognitive Sciences, edited by I. Cross and I. Deliège. Contemporary Music Review. London: Harwood Press. 207-220.
Clynes, M. (1983) Expressive Microstructure in Music, liked to Living Qualities. In: Studies of Music Performance, edited by J.Sundberg . Stockholm: Royal Swedish Academy of Music, No. 39.
Clynes, M. (1987) What can a musician learn about music performance from newly discovered microstructure principles (PM and PAS)? In A. Gabrielson (ed.) Action and Perception in Rhythm and Music, Royal Swedish Academy of Music, No. 55.
Cohen, D., R. Granot, H. Pratt & A. Barneah (1993) Cognitive Meanings of Musical Elements as Disclosed by Event-relatated Potential (ERP) and Verbal Experiments. Music Perception 11(2). 153-184.
Cooper, G. & L. B. Meyer (1960) The rhythmic structure of music. Chicago: University of Chicago Press.
Dannenberg, R. B. (1988) Real-time schedulingn adn computer accompaniment. In Current Directions in Computer Music Research, edited by M. V. Matthews & J. R. Pierce. Cambridge, Mass.: MIT Press.
Dannenberg, R. B. (1989) The Canon score language. Computer Music Journal 13(1): 47-56.
Dannenberg, R. B. (1992) Time Functions, letter. Computer Music Journal, 16(3), 7-8.
Dannenberg, R. B., Desain, P., & Honing, H. (in press) Programming language design for music. In G. De Poli, A. Picialli, S. T. Pope, & C. Roads (eds.), Musical Signal Processing. Cambridge, Mass.: MIT Press.
Dannenberg, R.B. & B Mont-Reynaud (1987) Following an improvisation in real-time. In Proceedings of the 1987 International Computer Music Conference. 241 - 248. San Francisco: International Computer Music Association.
Dannenberg, R.B. (1993) Music Understanding by Computer. In Proceedings of the IAKTA Workshop on Knowledge Technology in the Arts. 41-55. Osaka: IAKTA/LIST.
Dauer, A.M.D. (1988) Derler 1: Ein system zur klassifickation von rhythmen. Jazzforschung/Jazz research, 20.
Davidson, J. (1991) The Perception of Expressive Movement in Music Performance. Ph.D. thesis, City University, London.
Desain, P. (1986) Graphical programming in computer music, a proposal. In P. Berg (ed.), Proceedings of the 1986 International Computer Music Conference. 161-166. San Francisco: Computer Music Association.
Desain, P. (1990) Lisp as a second language: functional aspects. Perspectives of New Music, 28(1), 192-222.
Desain, P. (1991) Parsing the parser. A case study in programming style. Computers in Music Research, 1(2), 39-90.
Desain, P. (1992a) A (de)composable theory of rhythm perception. Music Perception, 9(4), 439-454.
Desain, P. (1992b) Can computer music benefit from cognitive models of rhythm perception? In Proceedings of the 1992 International Computer Music Conference. 42-45. San Francisco: International Computer Music Association.
Desain, P. (1993) A connectionist and a traditional AI quantizer, symbolic versus sub-symbolic models of rhythm perception. Contemporary Music Review, 9, 239-254.
Desain, P., & H. Honing (1992d) Response to Dannenberg (1992). Computer Music Journal, 16(3), 8.
Desain, P., & Honing, H. (1988) LOCO: a composition microworld in Logo. Computer Music Journal, 12(3), 30-42.
Desain, P., & Honing, H. (1989a) Report on the first AIM conference. Perspectives of New Music, 27(2), 282-289.
Desain, P., & Honing, H. (1989b) Quantization of musical time: a connectionist approach. Computer Music Journal, 13:56-66.
Desain, P., & Honing, H. (1991a) Quantization of musical time: a connectionist approach. In P.M. Todd and D. G. Loy (eds.), Music and Connectionism. Cambridge: MIT Press.
Desain, P., & Honing, H. (1991b) Towards a calculus for expressive timing in music. Computers in Music Research, 3, 43-120.
Desain, P., & Honing, H. (1992a) Music, mind and machine, studies in computer music, music cognition and artificial intelligence. Amsterdam: Thesis Publishers.
Desain, P., & Honing, H. (1992b) Musical machines: can there be? are we? Some observations on- and a possible approach to- the computational modelling of music cognition. In C. Auxiette, C. Drake, & C. Gérard (eds.), Proceedings of the Fourth International Workshop on Rhythm Perception and Production. 129-140. Bourges.
Desain, P., & Honing, H. (1992c) Time functions function best as functions of multiple times. Computer Music Journal, 16(2), 17-34.
Desain, P., & Honing, H. (1993a) Letter to the editor: the mins of Max. Computer Music Journal, 17(2), 3-11.
Desain, P., & Honing, H. (1993b) Tempo curves considered harmful. In "Time in contemporary musical thought" J. D. Kramer (ed.), Contemporary Music Review. 7(2). 123-138.
Desain, P., & Honing, H. (1993c) CLOSe to the edge? Multiple and mixin inheritance, multi methods, and method combination as techniques in the representation of musical knowledge. In Proceedings of the IAKTA Workshop on Knowledge Technology in the Arts. 99-106. Osaka: IAKTA/LIST.
Desain, P., & Honing, H. (1993d) On Continuous Musical Control of Discrete Musical Objects. In Proceedings of the 1993 International Computer Music Conference. San Francisco: International Computer Music Association.
Desain, P., & Honing, H. (1994a) Advanced issues in beat induction modeling: syncopation, tempo and timing. In Proceedings of the 1994 International Computer Music Conference. 92-94. San Francisco: International Computer Music Association.
Desain, P., & Honing, H. (1994b) Does expressive timing in music performance scale proportionally with tempo? Psychological Research, 56, 285-292.
Desain, P., & Honing, H. (1994c) Rule-based models of initial beat induction and an analysis of their behavior. In Proceedings of the 1994 International Computer Music Conference. 80-82. San Francisco: International Computer Music Association.
Desain, P., & Honing, H. (1994d) Can music cognition benefit from computer music research? From foot-tapper systems to beat induction models. In Proceedings of the ICMPC 1994. 397-398. Liège: ESCOM.
Desain, P., & Honing, H. (1994e) Shoes News, E-mail document.
Desain, P., & Honing, H. (1995) Computational models of beat induction: the rule-based approach. Proceedings of IJCAI 1995. Montreal: IJCAI.
Desain, P., & Vos, S. (1990) Autocorrelation and the study of musical expression. In Proceedings of the 1990 International Computer Music Conference. 357-360. San Francisco: Computer Music Association.
Desain, P., and H. Honing (in press) Towards algorithmic descriptions of continuous modulations in musical parameters. In Proceedings of the 1995 International Computer Music Conference. San Francisco: International Computer Music Association.
Desain, P., Honing, H., Dannenberg, R., Jacobs, D., Lippe, C., Settel, Z., Pope, S., Puckette, M., & Lewis, G. (1993) A Max Forum. Array, 13(1), 14-20. Also published as: Putting Max in Perspective. Computer Music Journal, 17(2), 3-11.
Deutsch, D. (1980) The processing of structured and unstructured tonal sequences Perception & Psychophysics, 28, 381-389.
Deutsch, D. (ed.) (1982) The Psychology of Music. New York: Academic Press.
Deutsch, D. and J. Feroe (1981) The internal representation of pitch sequences in tonal music. Psychological Review, 88, 503-522.
Dowling, W.J. & D. Harwood. (1986) Music Cognition. New York: Academic Press.
Drake, C. and C. Palmer (1991) Recovering structure from expresssion in music performance Proceedings of Cognitive Science, Chicago.
Drake, C. and C. Palmer (1993) Accent Structures in Music Performance. Music Perception. 10 (3) 343-378
Dürr, W, Gerstenberg, W., & Harvey, J. (1989) Rhythm (entry). In The new Grove dictionary of music and musicians. Stanley Sadie (Ed.). London : Macmillan, 1989.
Egmond, R. & D. Butler (1995) Key and mode connotations of pitch-class sets. In Proceedings of the 1995 Conference of The Society for Music Perception and Cognition.
Epstein, D. (1994) Shaping time. New York: Schirmer.
Feldman, J. , Epstein, D. & Richards, W. (1992) Force Dynamics of Tempo Change in Music. Music Perception, 10(2), 185-204.
Fodor, J. (1975) The Language of Thought. New York: Crowell.
Forte, A. (1973) The structure of atonal music. London: Yale University Press.
Fraisse, P. (1982) Rhythm and tempo. In D. Deutsch (ed.) The Psychology of Music. New York: Academic Press.
Friedman, D. P., M. Wand and C. T. Haynes (1992) Essentials of Programming Languages. Cambridge, Massachusetts: MIT Press.
Fritsch, I. (1979) Die Solo-Honkyoku der Tozan-Schule. Studien zur traditionellen Musik Japans. Band 4. Kassel: Bärenreiter.
Gabrielsson, A. (1974) Similarity ratings and dimension analyses of auditory rhythm patterns. II. Scandinavian Journal of Psychology. 14, 161-176.
Garner, W.R. (1974) The Processing of Information and Structure. New York: Wiley.
Garton, B. (1992) Virtual Performance Modelling. Proceedings of the 1992 International Computer Music Conference. San Francisco: ICMA.
Gjerdingen, R. O. (1994) Apparent motion in Music?. Music Perception. 11(4). 225-370.
Gutzwiller, A. (1983) Die Shakuhachi der Kinko-Schule. Studien zur traditionellen Musik Japans. Band 5. Kassel: Bärenreiter.
Hall, J.A. (1990) Seven Myths of Formal Methods. IEEE Software, Sept. 1990, 11-19.
Handel, S. (1989) Listening. An introduction to the perception of auditory events. Cambridge, MA. : MIT Press.
Handel, S. (1992) The differentiation of rhythmic structure. Perception & Psychophysics. 52: 497-507
Heuer, H. (1991) Invariant relative timing in motor-program theory. In J. Fagard & P. H. Wolff (eds) The development of timng control and temporal organisation in coordinated action. 37-68. Amsterdam: Elsevier.
Hewlett, W. B. & E. Selfridge-Field (eds) (1995) Center for Computer Assisted Research in the Humanities Cataloque. Menlo Park: CCARH.
Honing, H. (1990) POCO: an environment for analysing, modifying, and generating expression in music. In Proceedings of the 1990 International Computer Music Conference. 364-368. San Francisco: Computer Music Association.
Honing, H. (1992) Expresso, a strong and small editor for expression. In Proceedings of the 1992 International Computer Music Conference. 215-218. San Francisco: International Computer Music Association.
Honing, H. (1993a) A microworld approach to the formalization of musical knowledge. Computers and the Humanities, 27, 41-47.
Honing, H. (1993b) Issues in the representation of time and structure in music. Contemporary Music Review, 9, 221-239.
Honing, H. (1995) The vibrato problem, comparing two solutions. Computer Music Journal, 19(3)
Hoopen, G. ten, Hilkhuysen, G., Vis, G., Nakajima, Y., Yamauchi, F. & Sasaki, T. (1992) A new illusion of time perception - II. Music Perception, 11(1), 15-38.
Janata, P. (1995) ERP Measures Assay the Degree of Expectancy Violation of Harmonic Contexts in Music. Journal of Cognitive Neuroscience 7(2), 153-167.
Johnson, M, L (1991) Toward an Expert System for Expressive Musical Performance. IEEE Computer (24)7. 30-34.
Jones, M.R. & M. Boltz (1989) Dynamic Attending and Responses to Time. Psychological Review. 96(3), 459-491.
Keene, S. E. (1989) Object-Oriented Programming in Common Lisp: A Programmer's Guide to CLOS. Reading, MA: Addison-Wesley.
Kiczales, G., J des Rivières & D. G. Bobrow (1991) The Art of the Metaobject Protocol. Cambridge, MA: MIT Press.
Kosslyn, S. M. (1994) Image and Brain. The Resolution of the Imagery Debate. Cambridge: MIT Press.
Kramer, J. D. (1988) The time of Music. New York: Schirmer.
Kronman, U. & J. Sundberg (1987) Is the musical ritard an allusion to physical motion? In A. Gabrielsson (ed) Action and Perception in Rhythm and Music. Royal Swedisch Academy of Music. No. 55, 57-68.
Krumhansl, C. (1979) The psychological representation of musical pitch in a tonal context. Cognitive Psychology, 11. 346-374.
Krumhansl, C. L. (1990) Cognitive Foundations of Musical Pitch. New York: Oxford University Press.
Laird, J., Newell, A. & Rosenbloom, P (1987) SOAR: An Architecture for General Intelligence. Artificial Intelligence. 33:1-64.
Large, E. W. & Kolen, J. F. (1994) Resonance and the perception of musical meter. Connection Science. 6(2,3)
Laurson, M., C. Rueda & J. Duthen (1993) The PatchWork Reference Manual. IRCAM Report.
Lee, C. S. (1985) The rhythmic interpretation of simple musical sequences: towards a perceptual model. In R. West, P. Howell, & I. Cross (eds.) Musical Structure and Cognition. 53-69. London: Academic Press.
Lee, C.S. (1991) The perception of metrical structure: Experimental evidence and a model. In P. Howell, R. West, & I. Cross (Eds.), Representing musical structure (pp. 59-127). London: Academic.
Lerdahl, F. & R. Jackendoff (1983) A Generative Theory of Tonal Music. Cambridge, Mass.: MIT Press.
Lewin, D. (1987) Generalized Musical Intervals and Transformations. London: Yale University Press.
Longuet-Higgins, H. C. (1976) The perception of melodies. Nature, 263, 646-653.
Longuet-Higgins, H.C. & C.S. Lee (1982) Perception of musical rhythms. Perception. 11, 115-128.
Longuet-Higgins, H.C. (1994) Unpublished computer program in POP-11, implementing the "shoe" algorithm.
Longuet-Higgins, H.C.(1987) Mental Processes. Cambridge, Mass.:MIT Press.
Loy, G. (1988) Composing with Computers - A Survey of Some Compositional Formalisms and Music Programming Languages. In Current Directions in Computer Music Research, edited by M. V. Matthews & J. R. Pierce. Cambridge, Mass.: MIT Press.
Massaro, D.W. and D. Friedman (1990) Models of Integration Given Multiple Sources of Information. Psychological Review, (97)2, 225-252.
Mathews, M. V. (1969) The Technology of Computer Music. Cambridge, Mass: MIT Press.
McAdams, S. & Bigand, E. (1993) Thinking in sound: the cognitive psychology of human audition. Oxford: Oxford University Press.
Michon, J. A. & J. L. Jackson (1985) Time, Mind, and Behavior. Berlin: Springer.
Michon, J.A. (1967) Timing in temporal tracking. Soesterberg: RVO TNO
Michon, J.A. (1975) Time experience and memory processes. The Study of Time, 2, edited by J.T. Fraser & N. Lawrence. Berlin: Springer Verlag.
Miller, B. O., D. L. Scarborough, & J. A. Jones (1992) On the perception of meter. In M. Balaban, K. Ebcioglu, & O. Laske (eds.), Understanding Music with AI: Perspectives on Music Cognition. 428- 447. Cambridge: MIT Press.
Nakajima, Y., Hoopen, G. & Van der Wilk, R. (1991) A new illusion of time perception. Music Perception, 8(4), 431-448.
Narmour, E. (1992) The Analysis and Cognition of Melodic Complexity: The Implication-Realization model. Chicago: University of Chicago Press.
Neumann, F. (1986) Ornamentation and improvisation in Mozart. New Jersey: Princeton University Press.
Newell, A. (1990) Unified Theories of Cognition. Cambridge, MA.: Harvard University Press.
Noorden, L.P.A.S. van, (1975) Temporal Coherence in the Perception of Tone Sequences. PhD Thesis. Eindhoven University of Technology, The Netherlands.
Oosten , P. van (1993) A Critical Sudy of Sundbergs' Rules for Expression in the Performance of Melodies. Contemporary Music Review, 9, 267-274.
Otten, R.H.J.M. and L.P.P.P van Ginneken (1989) The Annealing Algorithm. Boston: Kluwer
Palmer, C. (1989) Mapping Musical thought to musical performance. Journal of Experimental Psychology, 15(12).
Palmer, C. and C.L. Krumhansl (1990) Mental representations of musical meter. Journal of Experimental Psychology: Human Perception and performance 16(4), 728-741.
Parncutt, R. (1994) A perceptual model of pulse salience and metrical accent in musical rhythms. Music Perception, 11, 409-464.
Partridge, T and Y.Wilks, (eds.)(1990), The foundations of artificial intelligence, a sourcebook. Cambridge: Cambridge University Press.
Partsch,H.A. (1990) Specification and transformation of programs : a formal approach to software development. Berlin: Springer.
Pennycook, B., D.R. Stammen, & D. Reynolds (1993) Toward a computer model of a jazz improviser. In Proceedings of the 1993 International Computer Music Conference. 228-231. San Francisco: International Computer Music Association.
Povel D.J. (1981) Internal Representation of Simple Temporal Patterns. Journal of Experimental Psychology: Human Perception and Production. 7(1).
Povel, D. J. (1977) Temporal structure of performed music: Some preliminary observations. Acta Psychologica 41, 309-320.
Povel, D.J. & P. Essens (1985) Perception of temporal Patterns. Music Perception. 2(4):411-440
Puckette, M. (1988) The Patcher. Proceedings of the 1988 International Computer Music Conference. San Francisco: ICMA.
Pylyshyn, Z. (1979) Complexity and the Study of Human Artificial Intelligence. In M. Ringle (ed) Philosophical Perspectives in Artificial Intelligence. New Jersey: Humanities Press, 23-56.
Pylyshyn, Z. W. (1984) Computation and Cognition: Toward a Foundation for Cognitive Science. Cambridge, Mass.: MIT Press.
Quatieri, T.F. and R. J. McAulay (1985) Speech Analysis/Synthesis Based on a Sinusoidal Representation. Technical Report 693. Cambridge:MIT.
Rasch, R.A. (1979) Sychronization in Performed Ensemble Music. Acustica 43(2).
Repp, B. (1990) Patterns of expressive timing in performances of Beethoven minuet by nineteen famous pianists. Journal of the Acoustical Society of America, 88, 622-641.
Repp, B. H. (1994) Relational Invariance of Expressive Microstructure Across Global Tempo Changes in Music Performance: An Exploratory Study. Psychological Research, 56, 269-284.
Rich, C. and R. Waters (1986) Readings in Artificial Intelligence and Software Engineering. Los Altos: Morgan Kaufman Pub.
Richie, G. D. and F. K. Hanna. 1990. AM: A Case Study in AI Methodology. In Partridge, D. and Y. Wilks, eds. The Foundations of Artificial Intelligence. A Source Book. Cambridge: Cambridge University Press.
Ringle, M. (1983) Psychological Studies and Artificial Intelligence. The AI Magazine, Winter/Spring. 37-43.
Roads, C (ed.) (1989) The Music Machine. Cambridge, Mass.: MIT Press.
Roads, C. & J. Strawn (eds.) (1985) Foundations of Computer Music. Cambridge, Mass.: MIT Press.
Rosenthal, D. (1992) Machine Rhythm: Computer Emulation of Human Rhythm Perception, Ph.D. Thesis, Massachusetts Institute of Technology
Ross, J. & Houtsma, A. J. M. (1994) Discrimination of auditory temporal patterns. Perception & Psychophysics. 56: 19-26
Rowe, R. (1993) Interactive Music Systems: Machine Listening and Composing. MIT press: Cambridge.
Rummelhart, D.E. & J.E. McClelland (eds.) (1989) Parallel Distributed Processing. Cambridge, MA: MIT Press.
Seashore, C. E. (1967) Psychology of Music. New York: Dover. (Originally published in 1938)
Serra, X. (1989) A system for sound analysis/transformation/synthesis based on a deterministic plus stochastic decomposition. Department of Music Report No. STAN-M-58, Ph.D. dissertation, Center for Computer Music Research in Music and Acoustics, Stanford University.
Sloboda, J. (1985) The Musical Mind: The Cognitive Psychology of Music. Oxford: Clarendon Press.
Smith, D.R. (1990) Kids, a semiautomatic Program Development System. IEEE transactions on Software Engineering. 16(9)
Smith, J. O. (1992) Physical Modeling Using Digital Waveguides. Computer Music Journal 16(4)
Steedman M. J. (1977) The perception of musical rhythm and metre. Perception, 555-569.
Stoy, J. E. (1977) Denotational Semantics: The Scott-Strachey Approach to Programming Language Theory. Cambridge, Massachusetts: MIT Press.
Strawn, J. (1989) Approximations and Syntactic Analysis of Amplitude and Frequency Functions for Digital Sound Synthesis. In C. Roads (ed.) The Music Machine. Cambridge: MIT Press. 671-692.
Sundberg & Verillo (1995) Comments on Feldman, Epstein & Richards (1992) Music Perception. 12(2), 265-266.
Sundberg, J. & Verillo, V. (1980) On the anatomy of the ritard: A study of timing in music. Journal of the Acoustical Society of America. 68, 772-779.
Sundberg, J., A. Askenfelt & L. Frydén (1983) Musical Performance: A synthesis-by -rule Approach. Computer Music Journal, 7(1)
Sundberg, J., A. Friberg & L. Frydén (1989) Rules for Automated Performance of Ensemble Music. Contemporary Music Review, 3.
Tennent, R.D. (1981) Principles of Programming Languages. London: Prentice Hall.
Todd, N. (1989) A Computational Model of Rubato. In "Music, Mind and Structure", edited by E. Clarke and S. Emmerson. Contemporary Music Review 3(1).
Todd, N. P. M. (1992) The dynamics of dynamics: a model of musical expression. Journal of the Acoustical Society of America. 91(6), 3540-3550.
Todd, N. P. M. (1993) Vestibular Feedback in Musical Performance: Response to Somatosensory Feedback in Musical Performance (edited by Sundberg and Verillo). Music Perception. 10(3), 379-382.
Todd, N. P. M. (1994) The auditory "primal sketch": A multi-scale model of rhythmic grouping. Journal of New Music Research, 23(1).
Todd, N.P. (1985) A model of expressive timing in tonal music. Music Perception, 3.
Todd, P.M. and D. G. Loy (Eds.)(1991) Music and Connectionism. Cambridge: MIT Press.
Vorberg, D. (1992) Response timing and synchronisation. In F. Macar, V. Pouthas & W. J. Friedman (eds) Attention and performance VII (535-555) Hillsdale, N. J.: Erlbaum.
Vos. P. & Handel, S., (1987) Playing Triplets: Facts and Preferences. In: Action and Perception in Rhythm and Music, Edited by A. Gabrielsson. Royal Swedish Academy of Music. No. 55.
Ward, J. O. (ed.) (1977) Concise Oxford Dictonairy of Music. Devon: Readers Union.
Watt, D.A. (1990) Programming language concepts and paradigms. London: Prentice Hall
Watt, D.A. (1991) Programming language syntax and semantics. London: Prentice Hall
Wilkes, Y. A. (1990) One small head: Models and theories. In D. Partridge & Y.A. Wilks (eds). The Foundations of Artificial Intelligence. 121-134. Cambridge University Press.
Wing, A. & Kristofferson, A. B. (1973) Response delays and the timing of discrete motor responses. Perception & Psychophysiscs, 14, 5-12.
Winskel, G. (1993) The formal semantics of programming languages: an introduction. Cambridge MA:MIT Press.