Keynote address, as presented at the ICMPC in Montreal, August 1, 1996.
We gratefully acknowledge the support of the Computer Music Center at the IBM T.J. Watson Research Center for this research.
Expression in music performance
This text is about the computational modeling continuous modulations in music performance, focussing on vibrato and portamento.The central question in this research is: is it possible to capture these expressive variations in pitch and amplitude algorithmically? And if so, what are the underlying rules and structural regularities?
In this lecture, we will concentrate on describing the methodology that allows for the modelling these modulations, in favor of presenting actual results. This methodology, we hope, could open up a whole new area of music performance research.
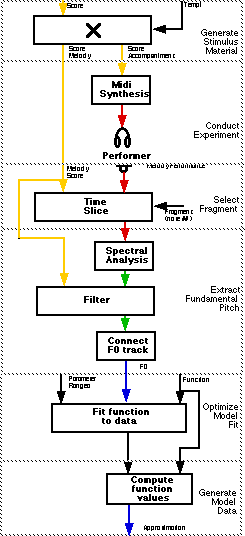
After a brief overview on existing music performance expression research, we will present related work on the study of vibrato and portamento. Then we will describe how to study continuous expression using an "analysis-by-synthesis" approach, how to analyse real performance data, and finally, present a method to actually model these modulations algorithmically.
This research is part of a larger project (Music, Mind, Machine) concerned with the computational modelling of music cognition, with an emphasis on the temporal aspects musical knowledge and music cognition. This study being one of the four domain studies to be further developped over the next five years.
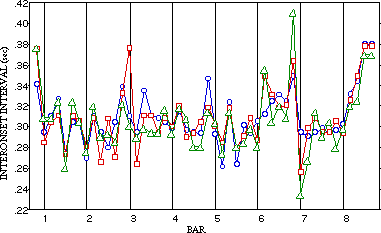
Music performance expression has been a topic of research for quite some time now. Most recently the work of, e.g., Clarke, Palmer and Repp gave us more understanding of the perception and performance of music. This research concentrates on the use of expressive timing and expressive dynamics in piano music. The availability of MIDI technology made it relatively easy to measure and quantify performance information, reducing piano notes to discrete note events of which the onsets, offsets and velocity can be studied. As an example, the expressive timing of the first eight measures of three repeated performances of a Beethoven composition is shown here:

This Figure shows the timing patterns of eight bars of a Beethoven Theme (three repreated performances, shown as duration versus metrical time). These timing variations were shown to be intented, musically meaningful and reproducable. The most important outcome is that a large amount of variability can be explained in terms of the musical structure -as conveyed by the performer to the listener-, be it global structure (like meter or phrase structure) or local structure (like chords or grace notes).
There are a number of computational models of expressive timing that make this relation explicit, all of them relating timing to one particular type of musical structure. They can generate artificial piano performances given a score and appropiate parameter settings of the model.
Sundberg (Sundberg, Askenfelt & Frydén, 1983) and colleagues constructed a rule-based system that deals mostly with the surface structure of the music. It consists of a relatively large collection of rules that can be applied to a score. Example of such a rule is "pitch-leap": delaying a note somewhat dependent on the preceeding interval.
Todd (1992) proposes a model of rubato related to phrase structure. The tempo over a phrase speeds up and slows down again, the amount of rubato being dependent on the position in the phrase hierarchy.
Clynes (1983) introduced the notion of a "composer's pulse".This is a discrete tempo pattern, repeated for each bar, different for each composer and time signature (e.g., Beethoven 6/8 pulse, Schubert 3/4 pulse). It is made up of hierarchical subdivisions of the bar recursively assigning unequal durations to each beat and sub-beat.
We have to note that these are partial models: they generate expression from one type of musical structure only. Although this research has been quite successful in explaining expression, there are still some interesting problems left:
First, a model of one type of expression clearly lacks: timing related to rhythmic structure. Remarkable since there is evidence that a large portion of the variance in an expressive performance can be related to rhythmic structure (as shown by Drake & Palmer, 1993).
Second, there is the problem of combining these models into one computational model. It is unclear how they interact?
Third, the problem of separating the components of expressive timing that originate from different sources. This is essential in making it possible to test these models empirically - a perfomer might make use of both metre and phrase structure (see, e.g., Clarke & Windsor, 1996).
Fourth,there are no models available of continuous expression. Unfortunate, to say the least, because it leaves out a whole variety of instruments in music performance studies (think, e.g., of voice, string and woodwind instruments).
We will address the latter gap in this paper, and focus on the use of vibrato and portamento in music performance.As illustration of the perceptual and musical importance of these continuous variations, a sound fragment:
This is a fragment played on a Theremin, an electronic instrument that is truely continuous: a tone generator of which the pitch and amplitude is continuously controlled by position of the hands with respect to two antennae. All the expression we hear is soly caused by continuous pitch and amplitude modulations.
Vibrato is made up of a different components, it is a composite of modulations of frequency, of dynamics, and timbre. We will restrict ourselves here to pitch vibrato, though a separation of these components is in fact is impossible. More precisely, we will look at pitch modulations, within and between notes. The main components of a pitch vibrato are: rate (or frequency), form (or shape of the vibrato) and extent (or amplitude of the vibrato).
There is a relatively small amount of literature on these aspects of music performance. Reasons could be the inaccesibilty for psychologists and musicologists to the data processing techniques needed or, the sheer amount of information present in these modulation signals. Compared to discrete data, there are many more degrees of freedom to explain.
Anyhow, there are enough interesting observations and hypotheses in the literature, though not always in agreement with each other. We mention those concerned with vibrato and portamento in singing.
Sundberg (1987), for instance, found that a singers rate of vibrato is fixed and independent of tempo. The rate being in a range of around. 4 to 7 Hz. Contrary, King & Horii (1993), found that singers can, and actually do change their rate.
Seashore (1936), pioneering in this subject, found that, on avererage, the rate at the begin and end of the note is the same. Prame(1984), in a study on vibrato rate of ten singers, found an increase of rate at end of notes, in the order of 15%. Vennard (1967) states, in a book on singing technique, that a good singer chooses the tempo in multiples of his/her vibrato.
If we look in more detail to the observations made for vibrato in note transitions, we find that most authors agree on the fact that a cycle is finished before making the transition. Still, they differ in describing in how that is obtained. The question still remains: how is a vibrato adapted to the length of the note:
Seashore (1967) states that the note is lengthed (or shortened) to accomodate a finished vibrato period. d'Allessandro & Castellengo (1991) say that the vibrato rate is adapted, such that a whole number of vibrato cycles fit in the note's duration. Yet another hypothesis could be, using Prame's (1984) observation of increasing rate towards the end of a note, to increase the rate such that full period is realised.
Another interesting observation, made by d'Allessandro & Castellengo (1991), is that in longer transitions the singer controls the vibrato such that the local slowing down of the vibrato are placed on harmonic important notes, the vibrato thus adapted to the harmonic context. Other studies also make the relation between pitch and the form of a pitch transition. Clynes (1987), for example, (besides -hardly suprising- proposing a composer-specific vibrato) hypothesizes that the shape of the vibrato in a transition is dependent on the direction and size of the pitch interval.
These are just a few hypothesis from the literature, and it is remarkable how much disagreement there is. A possible source for this disagreement could be sought in the measurement and analysis techniques used. Another source of confusion is mixing observations with estethics and aspects of musical style.
"The smile and the vibrato. We have a good analogy in the smile. The smile is nature's outlet for good will, the attitude of "I like you," "I like it," or "I am well disposed." [...] So it is with the vibrato. The pulsating quality is nature's language which tells the truth. It can be imitated, but the imitation is discernible. [...] The analogy between the smile and the vibrato is fundamental. They are the natural expression of well-being, good will, and genuine feeling." Seashore, C. (1936, p.111)
Seashore and his colleagues collected a wealth of data on the use of vibrato in different instruments. However, they sometimes tend to be normative, making statements of what is a good and what a bad use of vibrato, using metaphor, up to the level of being moralistic. Their work, though, still serves as a rich source of information.
Interesting is a classification of types of portamento in singing, all finishing the vibrato period before making a transition.
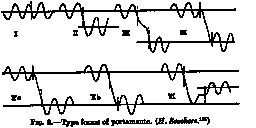
This Figure shows the six types of portamento Seashore and his colleagues found in their data. Though this is not actually a model of portamento, we can interpreted the axis and listen to them:
And Portamento type Va:
Subtle, though significantly different transitions.
Note: The schematic diagrams in this paper will show how the sound examples were made in the POCO system. The diagram below shows a Portamento pitch trajectory (blue) is combined with a static timbre yielding a dynamic spectrum (green), that is than converted into an audio signal (red).
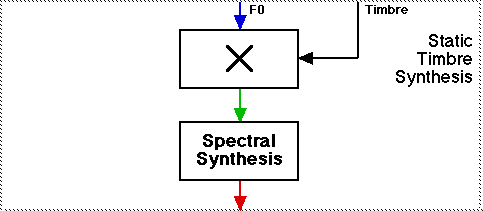

Diagram showing how the Portamento examples were generated.
Seashore made a contraption to listen to different types of vibrato in order to perceptually evaluate them, a so called "vibrato siren." With recent technology this is much simpler to realise this and perceptual judments can easily be made. We can use this "analysis-by-synthesis" method for the Saint-Saëns fragment, using a simple model of a constant vibrato regardless of the note material (much like a commercial synthesiser). Below a sinusoidal vibrato with a constant frequency and amplitude applied to the melody of 'Le Cygne,' and below it the diagram showing how the example was generated:
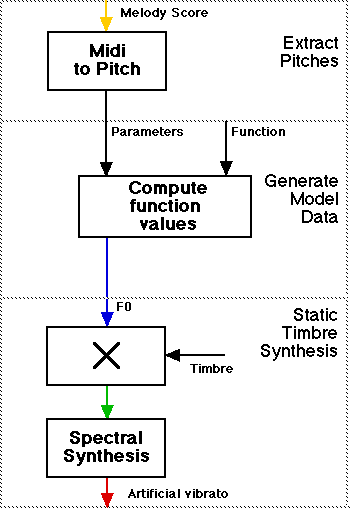

The synthesis of the model-based transitions.
This was a simple artificial performance, as comes out of any synthesizer without much effort. We will now illustrate the variety of continuous expression in real performances that we are trying to explain. The audio examples below were taken from different recordings of the same piece by Saint-Saëns for different instruments. The piece 'Le Cygne' from Carnival des Animeaux' was originally written for cello, but recordings are available for many instruments (at some cost). Try to ignore the vast differences in interpretation, and arrangement, but listen to the different ways in which vibrato is used and how different it is for the different instruments:
On string instruments, because of the sharp resonances in the body of the instrument, an applied pitch modulation immediately gives rise to a corresponding modulation in timbre and thus indirectly to a modulation in loudness. The discussion whether pitch and amplitude modulations, vibrato and tremolo are in or out of phase becomes a non-issue. Depending on the sharp resonance peaks of the body of the instrument in relation to the position of the harmonics both situations my occur and even a variation in overall amplitude that has the double frequency of the pitch variations may occur. In wind instruments the modulations in loudness are under more direct control and are more extensively used than pitch modulations in these performances.
In general, it is hard to listen analytically to such fast modulations, a perceptual integration takes places that makes vibrato almost a timbral issue: differences between types of vibrato and portamento are easily perceived but hard to relate to the actual form of the fluctuations in pitch. For example, it is hard to conclude, by listening alone, whether the vibrato rate actually drops during transitions for singers as is claimed by some authors. Likewise, it is hard to state whether there was a vibrato during a short transition in the cello piece, or how large the extend of a vibrato was (there is evidence that it is underestimated consistently). Seashore advocates listening to recordings played back a slow speed to gain insight in these questions.

Time stretching of audio.
Nowadays we can do a bit better by analyzing sounds spectrally, slowing down the data in the spectral domain and resynthesizing. In that way a slow version of the performance can be obtained without a corresponding drop in pitch. The next example consists of a few notes of the cello performance slowed down two and four times. Maybe focus your attention on the extend, the depth of the vibrato. (Don't be distracted by some artifacts generated by the signal processing applied to the percussive piano accompaniment as well. The small river in the background is caused by these artifacts.)
However revealing these slow performances are, there is no substitute for real measurements, and we can look at the spectrum evolving over time as it is the result of the spectral analysis, in the hope we can extract the fundamental pitch. Seashore did this with a photo mechanical contraption which outputted a kind of spectrum. By hand he traced the pitch trajectories of the fundamental and he then made 'performance scores' by annotating them with the actual notes played. In accordance with his method we start with computing time varying spectrum too:
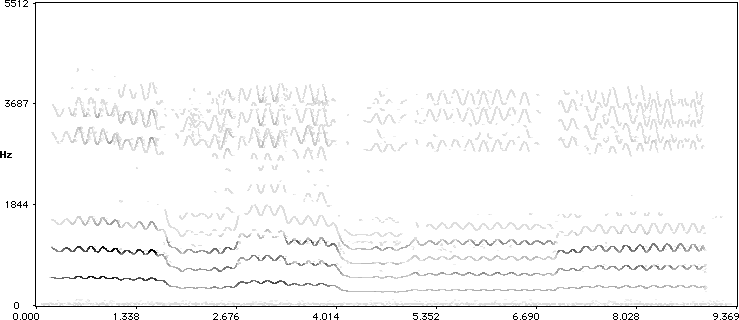
In this Figure the spectrum of a soprano voice singing the first phrase of 'Le Cygne' is shown. In fact, wherever there were nearby spectral peaks in subsequent time frames, they were connected to form trajectories over time. We can see the fundamental pitch and the harmonics. At this point we would like to acknowledge the great help that the shareware program Lemur has been to us to conduct all this signal processing. But even with this help, it is still not a trivial task to extract the fundamental pitch, it may not even be a strong component in the spectrum.
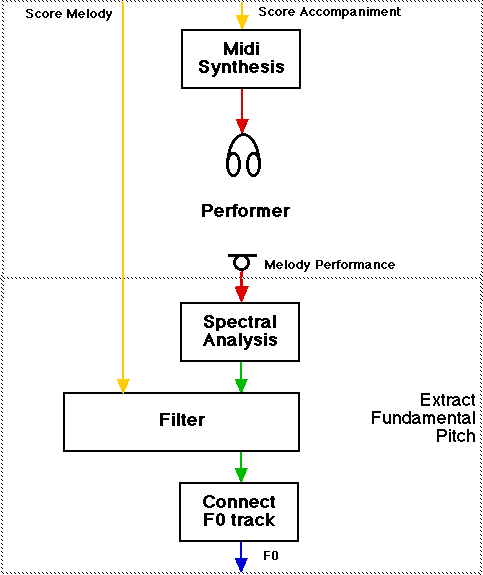

Extracting the fundamental frequency.
There are models that can tackle this problem, but we decided to take another route, because in this case we were collecting the data ourselves. By presenting a fixed accompaniment to the performer on headphones, we know at each point in time what pitch to expect - so we could simply filter the spectrum around the pitches of the melody.
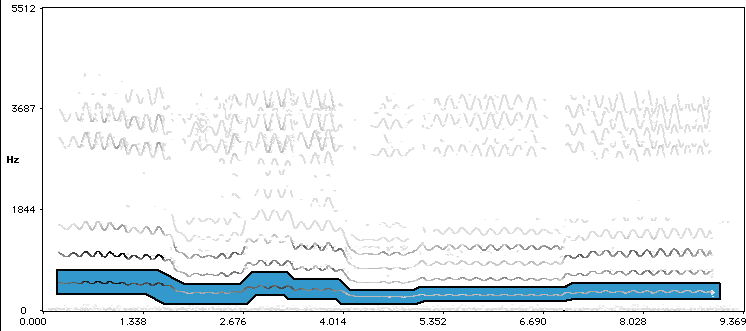
Only the blue part comes out of the filter. This is a great trick in studying the audio signals: keep a consistent symbolic MIDI-like representation at hand, even if it is only a rough one. This will simplify many of the methodological problems, as we will see later.
In this extracted area, usually there is just one frequency trajectory, possibly broken in silent passages. Collecting these into a table of f0 measurements then becomes trivial. The next animation shows this extracted fundamental as it changes over time for a fragment sung by one of our subjects (we are thankful to Robert Rowe and the faculty of NYU to supply us with such good subjects).
Note that next to fundamental pitch, a measure of the overall loudness can be obtained - which of course is needed for our modeling effort as well. But today we will only concentrate on pitch modulations.
The question arises how much reduction we are making? The fundamental pitch trajectory contains certainly vibrato and portamento, intonation is retained, and expressive timing is retained to a certain degree, as far as there are changes in pitch to signal the onsets of new notes. But all loudness and timbral information is lost. As one of our motto's is "always listen to your data," below a resynthesized version of the same fragment using the same static timbre you heard in previous examples. So the changing information that you will be hearing is only the pitch trajectory:
We think it is amazing how much musical information is still retained in this much reduced version of a performance, especially if one compares it to the wholly synthetic vibrato and portamento that was played before. The same point, how much expression is inherent in these continuous modulation, was also illustrated by the first audio fragment of a Theremin, an instrument that only has pitch and amplitude controls, but still is highly expressive.
So now we are all set for a more systematic approach to test the hypotheses. We will focus on the one question of how vibrato is adapted to global tempo. Maybe it is not at all, it just continues on, maybe it is only in the note onset that it is controlled and restarted at a specific phase, maybe the duration of the notes are adapted (the offset delayed) to the vibrato rate such that a whole number of cycles fit in, maybe it is the other way around: the vibrato rate is adapted to the note duration such that a whole number of cycles fits in, maybe that adaptation is only done towards the end of the note. These are our hypothesis and we conducted an experiment with professional performers on different instruments, using only the first phrase of the Saint-Saëns piece.


Experimental Setup.
In each trial the subject heard a warning tone. Then an artificially generated piano accompaniment in a specific tempo and was presented on a little earphone in one ear Subjects were instructed to play the melody along, The responses were recorded onto DAT tape for later analysis. The warning tone was also presented to a loudspeaker such that a proper alignment, synchronization of responses on DAT tape and stimulus material in MIDI file was guaranteed. Seven tempo conditions were used in small steps from 55 to 67 quarter notes per minute, with the 4 repetitions blocked per tempo.
In the interview after the experiment the performers all stated that neither the mechanical nature of the performance, nor the synthesized piano sound nor the earphone prevented them from playing naturally, though it must be said that all had experience in contemporary computer music performances in which these ingredients are not uncommon. Furthermore, for a steadily floating swan there is no real need for tempo changes and deep rubato. But it must be said that exactly the same setup could have been used with a midi recording of a live performance of the piano accompaniment. However, we wanted the consistent local tempo on a fine scale that was possible with the mechanical performance.
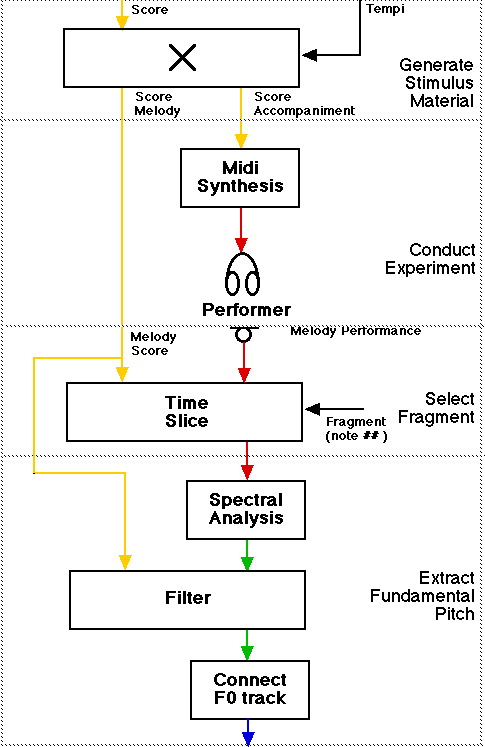

Obtaining data to analyse consistency over repeated performances and tempi.
The score is not only handy as filter, but also to collect the data for each trial and each transition within each trial, see the little slicing block in the diagram above.
The first question we have to ask is how much are these aspects under control of he performer. Because if they aren't, then there is no need to further investigate the hypothesis. The next animation shows the data of repeated performances of the same transition (between notes 5 and 6) at the same tempo (59). Three of the repetitions will be very similar, both to the eye and the ear, the fourth is quite different:
In general we found indeed that there is an amazing consistency. However, much concentration is needed for the performance task, and it seems that subjects needed quite some time to get used to the tempo - and blocking per tempo is essential - in a next study we will use even more repetitions. Thus, if vibrato and portamento is controllable indeed, we now have to tackle the question in what way it is controlled, and what are good rules or functions describing these transitions.
We are slowly building a library of useful functions, starting from the ones we designed for the Seashore prototypes, usually combining a transition component and a vibrato component in an additive way, and defining the functions such that they have parameters to describe the rate and change of rate, and the extend and change of extend through the note and the transition.
These functions, or algorithmic models, are then fitted to the data by an optimization procedure that walks through parameter space and from each position tests the direction in which the fit of model and data becomes better, climbing the hill always in the direction in which it is steepest.
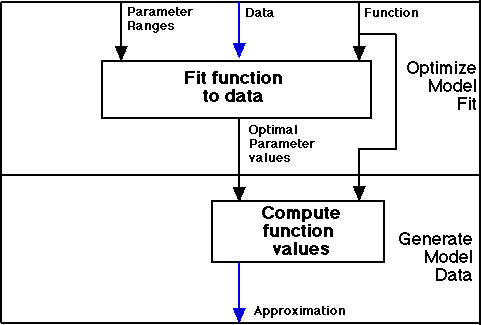
Optimizing model to the data.
This process will slowly converge to an optimal solution, as illustrated by the next Figure. The red line is performance data, first green line is first guess of parameter values, each iteration the parameters are changed a bit in the direction which yields the best results. Finally, a close match is found.
Because the search space of these fits is ill-formed, the landscape has many peaks, there can be locally optimal points for which any small adjustments of parameters will yield a worse fit, and yet a much better fit, a higher peak may exist at a remote point in parameter space. Therefore we use simulated annealing as our method which will, in the beginning of the search allow for many random excursions from the present point in parameter space, and then slowly lowers the extend to which these large steps may occur. This quite robust method yields reliable optimal parameters even in difficult cases.

Optimizing model to repeated performances and performances at different tempi.
Having these functions, these models fitted to the data now also allows us to average over repeated performances. We cannot do that on the raw data because, e.g., the average of two vibrati with a slightly differing frequency will give rise to a cancellation. But having fitted the same function to two performances and having gained two slightly differing frequency parameters, it is very well possible to average these parameters themselves and generate an average approximation.
But lets now move on to the real question of the dependency of vibrato and portamento on tempo. Using the same procedure we can collect performances at different tempi of the same transition: they look like this: first tempo 55 then 57, and so on, till 67 quarter notes per minute:
We see a slow rise of extend in onset in a couple of cycles which is characteristic for this specific transition and a drop of cycle at the fast tempo. This representation, of a surface, is what we find a very useful concept in the characterization of behavior in time, not only is there behavior evolving over time, as given in each one of these curves, but there is also behavior depending on the amount of time available for the behavior. We have developed this representation first for use in the control of synthesis in Computer music, using so-called generalized time functions or functions of more kinds of time (Desain & Honing, 1992).
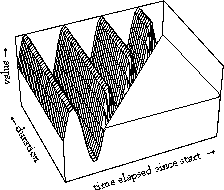
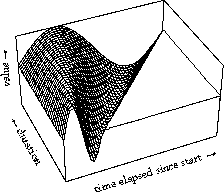
Above two variants are shown: a simplistic sinusoidal vibrato, adding more period for longer notes, and a sinusoidal glissando that is being stretched for longer durations. The axes are same as in the animation: time and duration. Each specific instance of a transition at a certain tempo is represented by one slice through the surface:
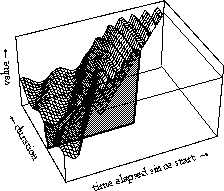
Now this concept comes in really handy in performance studies, because instead of fitting a one-dimensional function to a data curve, we fit a two-dimensional function to a data surface. This is right where we are in our research: we are working on the formalization of functions to describe these surface. We understand that you want to hear definitive conclusions about the hypothesis, but we simply don't have them yet.
Before we end, we mention briefly some practical technological applications of this work. The most obvious is the control in synthesizers and computer music systems that usually have only one vibrato rate, vibrato onset delay and a portamento speed control. We need to supply much means for much finer control for performing musicians here. With the advent of physical modeling synthesizers, in which. real body resonances are simulated for the string instruments: a good vibrato will automatically give rise to rich timbral modulations in proper relation with the pitch fluctuations.
Another application lays in extraction of fundamental pitch in real-time as some audio-to-MIDI converters attempt to do. A good model of the vibrato that is to be expected for the specific instruments makes the task of tracking pitch fluctuations and the decision when a new note starts much easier.
When we started this work, or better, when we were drawn into it because the questions are so tantalizing and our knowledge about these aspects of expression is so limited, we had the fearful feeling of embarking upon yet another domain, widening our field maybe too much. That may be a familiar feeling to many of you.
However, recently we realized that the approach we took now neatly folds the domain back into better know fields. That is because a computational modeling approach, fitting functions to data, will eventually come up with a set of parameters that vary only per note, or per transition. In other words: we are back in a discrete type of expression. Just like a value for tempo or loudness per note we now have some extra attributes that describe what happen within a note and during the transition between notes. The graphs look again similar to timing curves and we can use the known methods and approaches developed for the study of expression in keyboard music.
We can even step back and ask if, and if so, then how, continuous types of expression are linked to large musical structural units and how these types of expression also help convey the structure of music to the listener. We are convinced that the answer to the if question is a yes, as is so perfectly illustrated by Clara Rockmore playing the Theremin (see animation below). And we see the quest for the answer to the 'how' question as a great challenge for the coming years.
Clarke, E. F. & W. L. Windsor (1996), Timing, Dynamics and Structure in Human and Algorithmic performances. Proceedings of the 4th ICMPC. Montreal: McGill University.
Clynes, M. (1983) Expressive Microstructure in Music, liked to Living Qualities. In: Studies of Music Performance, edited by J.Sundberg. Stockholm: Royal Swedish Academy of Music, No. 39.
Clynes, M. (1987) What can a musician learn about music performance from newly discovered microstructure principles (PM and PAS)? In A. Gabrielson (ed.) Action and Perception in Rhythm and Music, Royal Swedish Academy of Music, No. 55.
d'Allessandro, C. & M. Castellengo (1991) Etudes, par la synthese, de la perception du vibrato vocal dans les transitions de notes. Bulletin d'audiophonologie 7: 551-564.
King, J. B. & Y. Horii (1993) Vocal matching of frequency modulation in synthesised vowels. Jounal of Voice 7: 151-159.
Prame, E. (1984) Measurements of the vibrato rate of ten singers. Journal of the Acoustical Society of America 96(4): 1979-1984.
Seashore, C. E. (1936) Psychology of the vibrato in voice and instrument. Studies in the Psychology of Music, Vol. III. Iowa: University Press.
Seashore, C. E. (1967) Psychology of Music. New York: Dover. (Originally published in 1938).
Sundberg, J. (1987) The Science of the Singing Voice. Dorkalb: Northern Illinois University Press.
Sundberg, J., A. Askenfelt & L. Frydén (1983) Musical Performance: A synthesis-by -rule Approach. Computer Music Journal, 7(1).
Todd, N. P. M. (1992) The dynamics of dynamics: a model of musical expression. Journal of the Acoustical Society of America. 91(6), 3540-3550.
Vennard, W. (1967) Singing, the mechanism and the technic. New York: Fisher.