Rhythmic aspects of vibrato
Peter Desain, Henkjan Honing, Rinus Aarts and Renee Timmers
[Desain, P., Aarts, R., Honing, H., & Timmers, R., (1999). Rhythmic Aspects of Vibrato. In Desain, P. and Windsor, W. L. (eds.) Rhythm Perception and Production (pp. 203-216). Lisse: Swets & Zeitlinger]
Introduction
Vibrato, the periodic fluctuation in pitch, amplitude, and/or timbre of a musical tone, is an important expressive component of musical performance. Especially singers and string players use vibrato to color tones. Physically, a separation can be made between pitch vibrato, amplitude vibrato and timbre vibrato. Perceptually, however, this separation is much more complicated. The different kinds of vibrato generally fuse into one percept of vibrato movement. However, experiments suggest that pitch fluctuations have the largest influence on the vibrato percept (Horii and Hata, 1988). In this paper, the term vibrato refers to pitch vibrato.
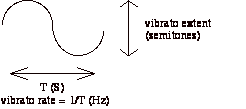
Figure 1. One vibrato period with sinusoidal shape and rate and extent indicated.
The physical characteristics of one vibrato period can be described by three parameters: its rate, extent and shape (see Figure 1). Most research on vibrato tries to relate measurements of these characteristics to performer, instrument, and style. The vibrato rate is generally around 6 to 7 Hz, but it can be as slow as 4 [CD example 1], or as fast as 12 Hz [CD example 2]. The extent of vibrato may become as large as 1.5 semitone (Castellengo, 1993). The shape of a period is generally sinusoidal. However, Horii (1989) made a classification of singer-vibrato-shapes into sinusoidal, triangular, trapezoidal, and unidentifiable.
Although it is useful to measure vibrato characteristics in relation to instruments, performers, and style, there is some evidence in the literature that musical and temporal structure play a role. Several observations have been made regarding the relation between vibrato and note on- and offsets. It has been found that a transition to another note always occurs in phase with the vibrato (d’ Alessandro and Castellengo, 1991; Sundberg, 1979): a note ascending towards the following note finishes with an ascending movement in the vibrato, and a note descending towards the following note finishes with a descending movement in the vibrato (see Figure 2). Sundberg (1979) suggested a mechanism behind this: singers adapt the point at which they start a note transition to the direction of this transition. In addition, it was found that for single notes singers generally start vibrato with a pitch increase (i.e. rising slope) (Horii, 1989).
In our point of view, these three observations suggest a tight relationship between timing and vibrato. It seems as if vibrato and rhythm are performed in close coordination, somehow resulting in a mutual dependency. Sound example 3 [CD example 3] shows what happens if no such relationship between vibrato and musical rhythm exists. This example is the first phrase of ‘Le Cygne’ by Saint-Saëns performed by a (programmed) synthesizer with continuous synthetic vibrato. One clearly hears that this sound example lacks expressiveness and musicality with respect to the use of vibrato.
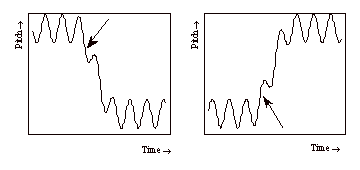
Figure 2. A note transition generally occurs in phase with the vibrato: a note descending towards the next note finishes with a descending movement in the vibrato (left), a note ascending towards the next note finishes with an ascending movement in the vibrato (right).
From this tight relation between vibrato and rhythm, the question arises whether the timing of notes is adapted to the vibrato, or vice versa[i]. If we assume the timing of notes to be fixed, a change of tempo should have an effect on the vibrato. When the tempo is increased, either the rate of the vibrato has to increase, or fewer cycles take place for any given note. However, it has been found (Seashore, 1932) that the vibrato rate of singers is fairly constant over different pieces and, we may conclude, therefore over different tempi. Furthermore, singers often report to have no conscious control over vibrato (Shipp, Sundberg, and Haglund, 1984) which suggests that they do not actively or consciously adapt vibrato to the timing of notes. In contrast, string players are said to have considerable control over their vibrato. Prame (1993) found a 15% increase of vibrato rate at the end of notes. This supports the notion that vibrato is adapted to the timing of notes (in this case note duration). Furthermore, Vennard (1967) suggests that singers decrease or increase their vibrato rate to conform to the duration of the note.
No conclusive results have been obtained in previous research. In this paper, an experiment is reported that addresses some of the contradictions. We look at some general performance characteristics, such as the consistency of vibrato over repetitions and between participant differences. The results of the experiment are used to obtain answers to four questions, related to the central issue described above: First, is there a specific vibrato before and/or after a note transition? Second, does global tempo influence vibrato rate? Third, how does vibrato develop during a note? Finally, is the vibrato rate adapted to the meter of the music? Adaptation of vibrato rate to the meter would mean coordination with tempo and some coordination with note timing as well.
Experiment
Five professional musicians participated in the experiment: a cellist, a oboist, a tenor, a thereminist, and a violinist. Each participant was paid for participation. A theremin is an electronic instrument controlled by moving both hands towards two antennas. The left hand determines the loudness of a continuous sine by moving up and down above a horizontal antenna. The right hand controls the pitch of the sine tone by moving forward and backward in front of a vertical antenna.
Recording took place in a soundproof cabin. Each musician was asked to play along with a metronomical accompaniment of the first phrase of ‘Le Cygne’ from “Le Carnaval des Animaux” by C. Saint-Saëns (see Figure 3). On the CD [track 4], the theremin performs the first five bars in tempo 60 (quarter note beats per minute).
This accompaniment was presented over headphones, and played on a Kurzweil K2500, using the standard piano sound. In front of the participant was a score of the melody of the first phrase. The phrase was repeated six times in ten different tempi, ranging from 54.5 beats per minute (bpm) to 68.6 bpm. The repetitions of the first phrase within one tempo were performed without pauses. Between such tempo-blocks there was a short break of two to three minutes. The total duration of the recording session was about one hour.
![]()
Figure 3. The score presented to the participants to read when performing the melody along with the accompaniment. The accompaniment was presented on headphones.
Data analysis
Performances were stored as 11 kHz, 16-bit,
mono audio files. A spectral analysis was run on each file using Lemur, a
Macintosh freeware program that connects spectral components that are close to
each other in time and frequency (Maher,
1989). The resulting file contains tracks for the fundamental frequency and
harmonics with a time resolution of about 3 ms. Because we are only interested
in pitch vibrato, the fundamental frequency gives enough information about rate,
extent and shape of each period of pitch vibrato. However, sometimes a higher
harmonic provides a more stable source of pitch information. This happens, for
instance, when on a string instrument the fundamental excites a sympathetic
resonance on another (open) string, causing two components (the main
fundamental and the resonance) to interfere in the same FFT frequency bin and
disturb the F0 track. In these cases, the fundamental was inferred from a
harmonic instead. A dynamic band-pass filter following the melody and picking
out the best harmonic was programmed to extract the fundamental frequency from
the Lemur file. This was done with POCO (Honing,
1990), a programming environment for the analysis of expression in music, using
Macintosh Common Lisp. The
continuous pitch data was subsequently low-pass filtered (below 10 Hz) with a third-order
Butterworth filter applied in two directions to achieve zero phase-shift. Next,
note onsets and offsets, as well as vibrato cycles had to be detected.
Half-cycles were detected between subsequent local maxima and minima, and these
were interpreted as vibrato when their rate was with the range of 2-10 Hz and
their extent was larger than 0.1 semitone. Note on- and offsets were detected
on the basis of a dynamic amplitude threshold (less than -40 dB as compared to
the maximum amplitude) in combination with a dynamic pitch threshold (less then
0.3 semitones deviation from the mean pitch).
Results
The consistency of vibrato rate and the control over vibrato was investigated in two ways. First, an ANCOVA was conducted to test the effect of tempo, repetition, note and the interaction of tempo and repetition on the mean vibrato rate per note. Tempo was taken as a covariate, while repetition and note were interpreted as factors. The reasoning behind this test is that when repetition and/or repetition * tempo have a significant effect on the vibrato rate, no control over the vibrato rate can be guaranteed. When, however, no significant effect is found for repetition and/or repetition * tempo on vibrato rate, a first indication of consistency (at least over repetitions) is provided. The results of the ANCOVA with tempo, repetition, note and repetition * tempo as independent variables and vibrato rate as dependent variable are shown in table 1.
Table 1. Analysis of covariance of vibrato rate
|
|
Cello |
Oboe |
Tenor |
Theremin |
Violin |
|
R2 |
0.6 |
0.51 |
0.18 |
0.60 |
0.62 |
|
p (ANCOVA) |
< 0.0001 |
< 0.0001 |
< 0.0001 |
< 0.0001 |
< 0.0001 |
|
Tempo p |
< 0.0001 |
< 0.0001 |
0.34 |
0.07 |
0.0004 |
|
Repetition p |
0.36 |
0.27 |
0.36 |
0.74 |
0.45 |
|
Note p |
< 0.0001 |
< 0.0001 |
< 0.0001 |
< 0.0001 |
< 0.0001 |
|
Repetition * tempo p |
0.28 |
0.27 |
0.27 |
0.8 |
0.42 |
For all instruments, no effect was found of repetition and repetition * tempo on vibrato rate. This indicates that all performers are in general consistent over repetitions. For the tenor, however, the R square is very low. The high variance not explained by the model (SS error = 513.9 vs. SS model = 113.3) indicates a general large variability in mean vibrato rate per note for the tenor.
The second way of analysis is by comparing repeated performances of the melody in each tempo visually. This gave a more clear insight into the consistency of vibrato. Figure 4 [CD track 5] shows that the violinist produces almost exactly the same vibrato on each repetition, while the tenor exhibits much greater variance. However, differences in vibrato consistency also occur between performances within one participant. For example, Figure 5 shows a consistent and an inconsistent performance of the oboist at respectively tempo 63.2 bpm and tempo 58.5bpm. These different degrees of consistency between and within participants can be explained in several ways. Low consistency could be an indication of lack of control over vibrato, or that vibrato does not need to be controlled in a consistent way for it to be perceptually acceptable. Differences within participants could indicate a varying ease of adapting the vibrato rate to tempo. Fatigue can also play a role in this, although the cello, theremin, and violin show consistent behavior over all conditions. Whether differences between participants are caused by performer or by instrument characteristics is unclear, as these factors are confounded (one performer per instrument).

Figure 4. Difference in consistency over repetitions between the violin and tenor (last note at 68.6 bpm).
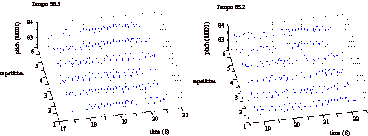
Figure 5. Difference in consistency over repetitions between two conditions for the oboe (last note).
Next, we investigated whether there is a specific vibrato phase before or after a note transition. In many cases we found the same behavior of vibrato at the end of notes as reported in the literature. For example, Figure 6 shows a transition between note 7-8 and note 8-9 for the oboe in tempo 61.5 in which the vibrato movement ends in the direction of the transition in the same way as reported by Sundberg (1979). In addition to Horii’s (1977) observations for single notes, we found that the vibrato at the beginning of single and leap notes tends to start with a pitch increase, as shown for the tenor in Figure 6.
However, an important problem arises with the
investigation of the vibrato phase at the beginning
and end of note transitions. It is very difficult to determine where a note
transition starts or ends. For example, one could conclude that the data shown
in Figure 7 (theremin) contradicts the findings by Sundberg. In this figure,
the transition from note 2 to note 3 is plotted for five different tempi (first
repetition) by the theremin. This picture seems to indicate that the vibrato
phase just before the descending note transition is between 270 and 360
degrees, which means a rising movement just before a descending note transition
[CD track 6]. However, the exact moment where the note transition starts is
very hard to determine.
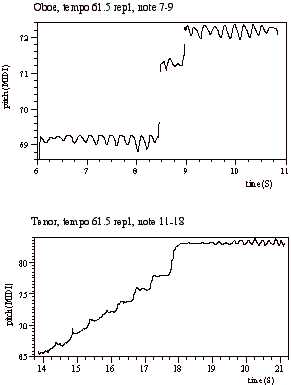
Figure 6. Vibrato phase at beginning and end of note. Top: direction of vibrato in phase with a note transition at the end of note for the oboe. Bottom: pitch increase at beginning of notes for the tenor. (Pitch is shown as MIDI key numbers [MIDI, 1996]).
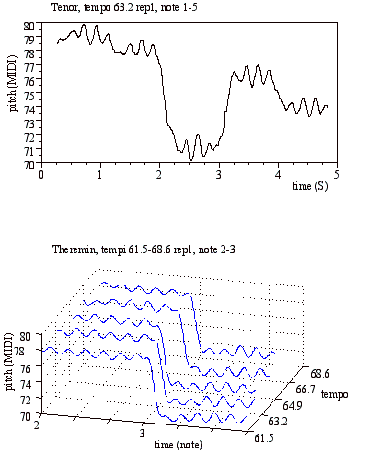
Figure 7. Vibrato
phase at beginning and end of note. Top: difficulty of determining the phase at
the beginning and end of note for the tenor. Bottom: vibrato phase at end of note for the theremin at
tempo 61.5,
63.2, 64.9, 66.7, 68.6 (front to back).
Figure 8 shows the relation between tempo and vibrato rate for each performer averaged over repetitions and notes. With a regression analysis a linear relationship between tempo and mean vibrato rate is tested. This relationship is significant only for the cello and oboe (p value is respectively <0.01 and < 0.0001). Figure 8 also provides some additional insight in the relation between tempo and vibrato rate, as a note may be performed with a whole number of vibrato cycles. When the tempo increases, and thus the note length decreases, the vibrato rate has to increase. However, there is a limit to this increase resulting in a drop of one cycle per note. The gray lines in Figure 8 indicate vibrato rates corresponding to 5, 6 and 7 cycles per quarter note.
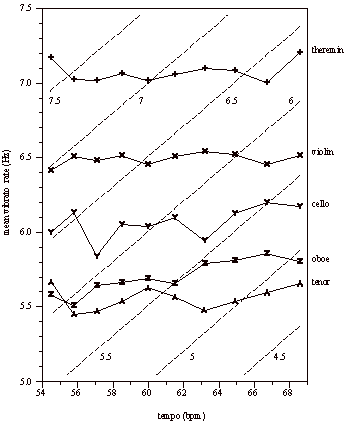
Figure 8. The relation between vibrato rate (averaged over repetitions and notes) and tempo for each instrument. The gray lines indicate the vibrato rate that corresponds to 5-7 cycles per quarter note. The numbers indicate the number of cycles per quarter note.
Figure 8 shows that participants used different strategies. Generally, all instruments produce a higher vibrato rate at high tempi with than at lower tempi. Within this trend, the vibrato rate of the cellist varies the most and the vibrato rate of the violin varies the least with tempo. The violinist has the most constant vibrato rate throughout the different tempi. The theremin has two wide peaks at the lowest and highest tempo and small differences between rate for middle tempi. At the two highest tempi, the vibrato rate of the theremin seems to scale with tempo. Furthermore, the theremin has very small variance within a tempo. The variance between tempi is larger.
The interpretation of these observations is not straightforward. For the cello and oboe, it seems as if the vibrato rate is adapted to tempo. For the other performers this is much less clear. The differences in mean vibrato rate between performers could explain this. For example, the theremin has a very high average vibrato rate (around 7 Hz). The chance for a whole number of small vibrato periods to fit in a note is greater than for long vibrato periods. It can therefore be expected that performers with low vibrato rates, like the cellist and oboist, exhibit more scaling than performers with high vibrato rates, such as the thereminist and violinist.
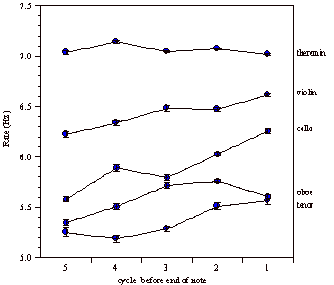
Figure 9. Vibrato rate (and standard errors) of the last five cycles before the end of notes averaged over tempo, repetition and notes for each instrument. The vibrato rate tends to increase towards the end of the note.
The interpretation of a small variance within one tempo should be made carefully. It can reflect two different strategies. The first one is that performers choose a vibrato rate for a block in the experiment (6 repetitions of the 4-bar phrase in one tempo) and try to remain close to this rate throughout the block to maintain continuity. The second interpretation is that the tempo of the block forces a certain vibrato rate, and this rate does not change much over repetitions because tempo remained the same throughout the block. So a small variance reflects either the ability of performers to remain close to a chosen vibrato rate, or a tight relation between tempo and vibrato rate. Further investigation is needed to distinguish between the two.
With respect to the development of vibrato within a note, Figure 9 shows the rate of the last five cycles before the end of the note, split per instrument and averaged over tempi, notes and repetitions. The graph shows mean rate with standard error bars. The cello [CD track 7], tenor, violin and to a lesser extent the oboe show an increase of rate towards the end of a note, which is in agreement with Prame (1994). As mentioned earlier, vibrato rate might increase to get a better chance of a desired vibrato phase at the end of the note. A regression analysis with cycles from end of note as predictor for the mean vibrato rate shows a significant positive linear relationship for all instruments (cello p < 0.0001, oboe p < 0.0001, tenor p < 0.0001, theremin p < 0.002, violin p < 0.0001). The slope of the line varies between 0.01 (for the violin and theremin) and 0.12-0.19 (for the oboe, tenor and cello). The slopes of the oboe, tenor and cello approximate Prame’s 15% increase of vibrato rate at the end of notes.
Finally, to see whether vibrato is synchronized to the pulse at a small metrical level the following measurement was made. For a certain metrical grid the phase of the vibrato cycle at each grid point relative to the onset of the vibrato cycle was measured. Then, frequency distributions were generated for each performer, with on the x-axis the phase from 0 to 1, and on the y-axis the number of times a phase occurred at all grid points. This measurement was done at the quarter, eight, sixteenth, and thirty-second note grid. The clearest results were obtained for the thirty-second note grid for the cellist, oboist, and thereminist, and are shown in Figure 10. As can be seen, both the cellist and oboist (and to a less extent the thereminist) have peaks in the frequency distribution, which indicates that a certain phase occurred more than others on the 32nd note grid. This peak lies around 0.4, 0.1, and 0.3 for respectively the cellist, oboist, and thereminist. The oboist exhibits the most stable pattern with changing tempo.
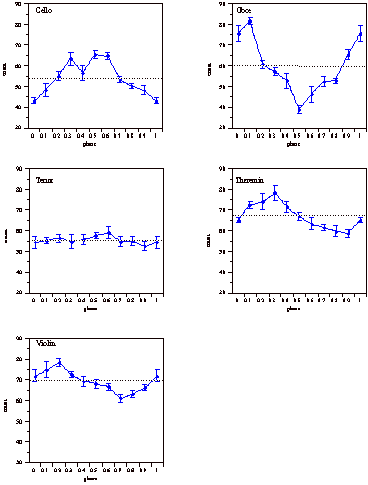 Figure 10. Frequency distributions of the vibrato phase at the 32nd note grid with
standard error bars.
Figure 10. Frequency distributions of the vibrato phase at the 32nd note grid with
standard error bars.
Summary
In this paper, an investigation of the rhythmic aspects of vibrato is presented. Five different musicians played six repetitions of a short melody in ten different tempi. By means of intensive data processing the detection of vibrato cycles and note on- and offsets was possible. Vibrato seems an important expressive component, to a great extent under the control of performers, but by its very fast and fusing nature not something that all performers are able to produce perfectly. An attempt to answer the question whether vibrato rate is adapted to tempo was made. A first indication of this relation is the confirmed relation between tempo and vibrato rate for instruments with a low vibrato rate. A second indication is the increasing vibrato rate towards the end of notes for all participants except the participant with highest vibrato rate (the theremin). Meter was found to be target of synchronization for the instruments that showed some scaling of vibrato rate with tempo. The vibrato rate of the tenor was too variable to be reliable for testing.
The analytic approach towards the performance of vibrato appeared to be fruitful and led to many ideas for further investigation (see Desain et al., in preparation). We conclude that temporal aspects of vibrato are indeed important aspects of vibrato, under considerable control of the performer. Temporal aspects are important in their relation to tempo and to the length of notes of the music, but insignificant in their relation to meter. In future investigations we hope to be able to explain the performance of vibrato by integrating knowledge about its production, perception and physics.
References
d’Alessandro, C., and Castellengo, M. (1991). Etude, par la synthese, de la perception du vibrato vocal dans les transition de notes. Bulletin d’Audiophonologie, Ann. Sci, Univ. Franche-Comte, 7, 551-564
Castellengo, M. (1993). Fusion or separation: From vibrato to vocal trill. Proceedings of the Stockholm Music Acoustics Conference.
Desain, P., Honing, H., Aarts, R., and Timmers, R. (in preparation). Continuous modulations in musical performance.
MIDI Manufacturers Association (1996). The complete MIDI 1.0 detailed specification version 96.1. La Habra: MIDI Manufacturers Association.
Honing, H. (1990). POCO: An Environment for Analysing, Modifying, and Generating Expression in Music. In Proceedings of the 1990 International Computer Music Conference. San Francisco: Computer Music Association.
Horii, Y. (1989). Frequency modulation characteristics of sustained /a/ sung in vocal vibrato. Journal of Speech and Hearing Research, 32, 829-836.
Horii, Y., and Hata, K. (1988). Phase relationships between frequency and amplitude modulations in vocal vibrato. Folia Phoniatr, 40, 303-311.
Maher, R.C. (1989). An approach for the separation of voices in composite musical signals. Ph. D. dissertation, Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign.
Prame, E. (1994). Measurements of the vibrato rate of ten singers. The journal of the Acoustical Society of America, 96(4), 1979-1984.
Seashore, C. E. (1932). The Vibrato. Iowa City, Iowa : Univ. of Iowa.
Shipp, T., Sunberg, J., and Haglund, S. (1984). A model of frequency vibrato. Transcripts of the 13th Symposium on care of the professional voice. L. van Larena (Ed.) (New Voice Foundation, New York), 116-117
Sundberg, J. (1979). Maximum speed of pitch
changes in singers and untrained participants. Journal of Phonetics, 7, 71-79.
Vennard W., and Leden H., (1967). The importance of intensity modulation in the perception of a trill. Folia phoniatricia, 19, 19-26