[published as: Desain, P, Honing, H, and Heijink, H. (1997) Robust Score-Performance Matching: Taking Advantage of Structural Information. in Proceedings of the 1997 International Computer Music Conference., 337-340 . San Francisco: ICMA.]
Robust Score-Performance Matching:
Taking Advantage of Structural Information
Peter Desain (1), Henkjan Honing (1, 2) and Hank Heijink (1)
NICI (1), University of Nijmegen
Music Department (2), University of Amsterdam
Abstract
Linking notes in a musical performance to the corresponding notes in a score, so-called score-performance matching, has been the topic of quite a large body of research. Proper matching algorithms are crucial for real-time composition and automatic accompaniment systems, as well as for music performance research and the design of expression editors. A matching algorithm is presented that takes advantage of the temporal structure that is annotated in the score. It is compared to two alternative matching procedures that use structural information only implicitly.
1 Introduction
The term matching refers to a procedure that links events (notes) in a musical performance to the corresponding events in the score. Proper matching algorithms are crucial for real-time composition and automatic accompaniment systems, where a "listening" machine has to find out where the musician is with respect to a known score, in order to make an appropriate musical response (like playing an accompaniment). In the context of music performance research, matching algorithms are necessary to be able to measure timing: it has to be known which performance note relates to which score note to be able to extract expressive timing patterns and calculate local tempo. The design of expression editors enabling the manipulation of performance characteristics is based on these expressive patterns, and score-performance matching thus becomes an essential pre-processing stage.
Although a listener reading the score along with the performance may be unaware of this, the matching problem is a complex task. There are several reasons for this. First, in the case of parallel voices, expressive timing may cause the order of events in the performance to be different from the order specified in the score. Secondly, the performer could omit, insert or change notes by mistake, often resulting in many alternative interpretations (matches), especially in the case of repeated notes on the same pitch. Thirdly, there may be events in the score that are not written out completely (e.g., certain kinds of ornaments). These difficulties cause the poor success of practical matching programs, and sometimes even an abandonment of the whole idea (Puckette & Lippe, 1992). The remarkable ease with which human listeners can follow a performed score inspired us to yet another attempt, based on ideas on mental representation of temporal structure that were developed in the context of studies on expressive timing in music (Desain & Honing, 1992).
Before describing three matching methods that somehow take advantage of the temporal structure in the score, we will explain the typical types of errors that occur in music performance.

2 Performance Errors
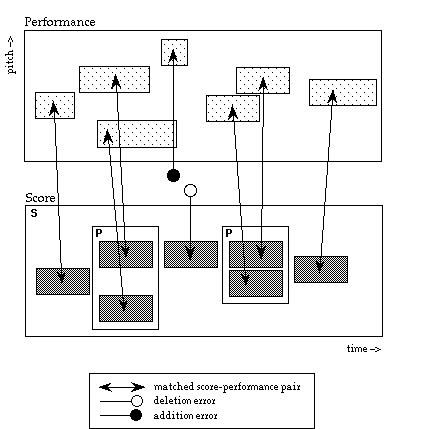
The matching problem would be simplified if we knew beforehand that a performance were flawless, i.e. without any wrong notes when compared to the score. However, even expert performers will make mistakes. While errors can come from different sources (see Palmer & Van der Sande, 1993), most matching algorithms can identify two types of errors: addition and deletion (see Figure 1). Deletion occurs when a note was not played in the performance but should have been, according to the score, and addition is the situation in which a note has been played that is not written in the score. Sometimes a combination of a deletion error and an addition error can be interpreted as an substitution error (e.g., playing a note at the expected time, but at the wrong pitch), but interpretation of errors is beyond the scope of the matchers discussed in this paper.
3 Matching Methods
Matchers are used in different contexts, and can be used for very different tasks. One category of algorithms focuses on real-time matching, often called score-following. Early work in score following was performed by Dannenberg (1984) and Vercoe (1984), both primarily interested in making real-time matchers. Dannenberg describes an algorithm solely based on pitch information, intended to robustly follow a monophonic instrument. Later these algorithms were extended to deal with polyphonic music and multiple instruments (see Grubb & Dannenberg, 1994 for an overview). Most algorithms primarily match pitch, possibly in combination with time information (An exception is Vantomme [1995] who proposes an algorithm using time information, resorting to pitch information only if this fails).
Another family of algorithms is concerned with off-line analyses, where the quality of the match is more important than efficiency or the fact that the match can be made in real-time. Below we discuss three proposals that, besides matching pitch, make use of temporal information present in the score: an incremental matcher that has a simple concept of structure (based on same/different score times), a non-incremental matcher that constructs a table ranking of all possible matches before selecting the best one, and a structure-based algorithm. The algorithms apply different match-rules and error-measures for events that happen at the same time in the score (e.g., chords, parallel voices) or in sequential order (e.g., melodies, runs of notes).
3.1 The Strict Matcher
A very simple matcher is the "strict matcher," part of the POCO environment (Honing, 1990; Desain & Honing, 1992). Its name is due to the fact that the order of the notes, as notated in the score, is "strict:" notes that have different subsequent score times should be performed in that order in the performance, while notes that have the same score times can occur in any temporal order.
The algorithm makes use of a window that is moved over the score while successive notes from the performance are given a chance to match the score notes in this window. The size of the window, a parameter of the algorithm, is measured in number of clusters: a cluster is either a single note, or several notes expected to happen at about the same time (e.g., a chord). A maximum-spread parameter determines when successive notes are still to be considered part of a cluster. The size of the window is important to the performance of the matcher. If the window is too small, the matcher will not deal well with deletion errors: if the match-to-be for the current performance note is outside the window, the matcher will think the performance note was an addition error instead. On the other hand, if the window is too large, an addition error may cause the matcher to look too far ahead, match the wrong performance note and skip part of the score.
The matcher places the window at the first score note and inspects the clusters in it. Then it takes the first note of the performance and tries to match it to the first score note in the window that matches its pitch. Either the note is matched to a score note, or it is discarded as an addition error, and then the algorithm proceeds with the next performance note. If the note can be matched, but the first note to match the performance note is in the second cluster (i.e., it has a later score time), the notes of the first cluster cannot be matched anymore, since the order specified in the score would be violated, and still&endash;unmatched score notes in that cluster are assumed to be deletion errors. In this way, the matching process continues until the end of the score or the performance is reached.
On the one hand, two performance notes can be matched to two score notes within the same score cluster, if their onsets differ no more than the maximum spread. On the other hand, there should be a certain amount of time between two consecutive notes (not belonging to the same cluster). This amount of time is controlled by the third parameter "minimum inter-onset interval."
The strict matcher has proven to perform well with expert performances, i.e., performances where addition or deletion errors occur only occasionally. However, even in these cases the method fails in situations where there is an error in the context of many repeated notes and in situations where there are parallel voices that are independently timed, and the order represented in the score is no longer respected. An improvement may be to specify the window size in real time instead of number of note clusters.
The matcher has a computational complexity smaller than w*c*O(n), where n is the number of notes in a performance, w is the window size (number of clusters) and c the maximum number of notes in a cluster. This will prove to be quite efficient when compared to the other two matchers.
3.2 The Tabular Matcher
Another approach is not to use a window, but to take all score and performance data into account, and construct a table that ranks all possible combinations (e.g., Large, 1993; Hoshishiba et al., 1996). We will refer to this idea as a "tabular matcher."
In Large’s (1993) algorithm, the performance is preprocessed to identify clusters (notes that happen around the same time, i.e. similar to the strict matcher method). Then, a table of n rows and m columns is constructed, with n being the number of clusters in the performance, and m the number of clusters in the score. The table will be filled with a measure of goodness of the match of each performance cluster with each score cluster. Neither Large (1993) nor Hoshishiba et al. (1996) give an exact definition of the measure of goodness they use. The table is then integrated backwards, i.e. from right to left and from bottom to top, in such a way that the best value, representing the goodness of the best match of the final fragment, is used to calculate the next larger table. This amounts to searching an optimal route through a network of possible matches. Using a representation administrating all matches at once in this way, reduces the computational complexity of the algorithm, in exchange for a higher memory cost. This technique is known as dynamic programming (see Cormen, Leiserson and Rivest, 1990).
Another important difference with the strict matcher is that clusters are matched instead of individual notes. This means that a performance chord of, say, three notes can be matched to a score chord of five notes. The matcher will compute a value for each note of the performance chord that can be matched to a note in the score chord in the same way as it would for a normal single match. These values are added, while a penalty is given for every performance note that cannot be matched. Evidently, the goodness measure plays a crucial role in the performance of the algorithm.
The tabular matcher has a complexity of O(m2*n). However, it could be made more efficient by not taking all possible matches into account, but only those in temporal proximity (a diagonal band in the table). The algorithm is essentially non-incremental, since the method needs all candidate matches before calculating the optimal one. Contrary to the strict matcher, the tabular matcher can handle errors in a better way and, in contrast with the other methods, notes with non-matching pitches can also be matched (see Large, 1993). However, it is unclear which goodness measure will give the best performance, and how it can be adapted to make better use of the structural context (i.e., is a note expected to be part of a chord, melody, trill, etc.).
3.3 The Structural Matcher
The structural matcher (Heijink, 1996) is based on the idea that temporal structure annotated in the score might give us more clues on how to interpret the performance. This is motivated by the observation that while expressive timing may greatly upset the order of events as specified in the score, it will mainly do so in ways respecting the musical structure (e.g., notes in a melodic line are not likely to be played in a different order, while notes in two parallel voices can easily occur in any order). If temporal structure (chords, voices, etc.) is annotated in the score, we can predict which order-constraints will probably be observed. In the case of performance errors, a larger set of possible matches may still need to be calculated. The structural annotation of the score also makes it possible to invoke specialized matchers, at appropriate times, to deal with more complex objects like ornaments.
We will restrict the discussion here to two types of temporal structure, annotated as S(equential) and P(arallel) in the score. A sequential object is a number of objects occurring one after the other (e.g., a melody). A parallel object is a number of objects occurring at the same time (e.g., a chord). Hence, a score can be represented as a tree where every node is either a structural unit (S or P) or a single note. A performance is merely a list of notes, ordered by onset time. This timing information is used in the matching process. For every note in the score, the matcher tries to predict which point in performance time will correspond with the onset time of the score note. The algorithm does this based on previous matches and structural information. A window is then placed on that point of time in the performance (not the score, as in the strict matcher) and the score note is matched with every note in the window with the same pitch. If there is no note of the same pitch in the window, the matcher concludes the score note has not been played and therefore is labeled as a deletion error. If there is just one note that matches the pitch of the score note, the matcher matches that note with the score note and moves on to the next score note. When there is more than one note that matches the pitch of the score note, multiple matches are instantiated. Thus, unlike the strict matcher, more matches are maintained for later evaluation, but unlike the tabular matcher not all are &endash; only those that fit the order constraints imposed by the type of structural annotation in the score.
The combinatorial explosion that could result from the representation of multiple matches (especially in the context of repeated notes) is again harnessed using dynamic programming, by recognizing when two independently developed matching strands arrive again at a same state where the same sets of performance and score notes are to be matched. At the end of the matching process there will be a network of possible matches from which the matcher has to choose the best one. Like the tabular matcher the choice is made in the following way: for every single match (a pair of one score note and one performance note) a goodness value is computed. This goodness value is based on the amount of time the performance note onset differs from the predicted onset of the score note, a prediction that is calculated on the basis of a small temporal context and thus makes use of structural information. For example, in the case of sequential structure local tempo is measured, while in the case of a parallel structure asynchrony is a better measure. Deletions and additions receive a penalty in their goodness.
After evaluating possible individual matches in this way, a optimal route through the network of partial matches is calculated, leading to an overall-best match.
The structure matcher can be seen as a crossbreed between the strict matcher and the tabular matcher. If the window is very large, the matcher will perform like the tabular matcher. With a small window, the matcher will look more like the strict matcher except that it uses pitch and onset information. It lifts the important restriction of the strict matcher that it cannot deal with independently timed parallel voices. Furthermore, it supports the use of the information in the score to select the appropriate matching-rule and goodness measure, allowing the matcher to be extended with sub-matchers that specialize in, for example, grace notes, trills, arpeggio’s, etc.
5 Further Work
To represent the output of the matcher, and the structural information needed at its input, we have developed a backward compatible extension of the standard MIDI file format in POCO. The approach maintains separate score and performance files, which are effectively "zipped" together into the internal representation needed in, for example, expression editors. It can represent performance errors.
The various matchers are available in POCO (https://www.nici.kun.nl/mmm/CODE/) and we are working on a version of POCO that can freely be accessed over the network.
6 Discussion and Conclusion
We have discussed several approaches to matching. The use of structural annotation in the score alleviates the problems of the other approaches and we think that there is not enough ground for the pessimism expressed by some authors at previous ICMCs. Although not all problems have been solved, robust score matching and score following seems feasible if we learn how to exploit more fully the link between the musical knowledge that is expressed or implied in musical scores, and the rendition thereof in music performance.
7 Acknowledgments
This research (part of the "Music, Mind, Machine" project at the Nijmegen Institute of Cognition and Information) is made possible by the Netherlands Organization for Scientific Research (NWO).
8 References
Cormen, T.H., C.E. Leiserson and R.L. Rivest (1990) Introduction to algorithms. Cambridge: MIT Press.
Dannenberg, R. (1984) An On-Line Algorithm for Real-Time Accompaniment. In Proceedings of the 1984 International Computer Music Conference. San Francisco: International Computer Music Association. pp. 193-198.
Desain, P. & H. Honing (1992) Music, mind and machine, studies in computer music, music cognition and artificial intelligence. Amsterdam: Thesis Publishers.
Grubb, L. & R. Dannenberg (1994) Automating Ensemble Performance. In Proceedings of the 1984 International Computer Music Conference. San Francisco: International Computer Music Association. pp. 63-69.
Heijink, H. (1996) Matching Scores and
Performances. Master’s thesis, Nijmegen University
(http:
//www.nici.kun.nl/mmm/PAPERS/HE-96-A.HTML).
Honing, H. (1990) POCO: an environment for analyzing, modifying, and generating expression in music. In Proceedings of the 1990 International Computer Music Conference. San Francisco: Computer Music Association. pp. 364-368.
Hoshishiba, T., S. Horiguchi & I. Fujinaga. (1996) Study of Expression and Individuality in Music performance Using Normative Data Derived from MIDI Recordings of Piano Music. In Proceedings . of the 4th International Conference on Music Perception and Cognition. Montreal. pp 465-470.
Large, E. W. (1993) Dynamic Programming for the Analysis of Serial Behaviors. Behavior Research Methods, Instruments and Computers 25(2). pp. 238-241.
Palmer, C. & C. van der Sande (1993) Units of Knowledge in Music Performance. Journal of Experimental Psychology: learning, Memory and Cognition, 19(2), pp.457-470.
Puckette, M. & C. Lippe (1992) Score Following in Practice. In Proceedings of the 1992 International Computer Music Conference. San Francisco: Computer Music Association. pp. 182-185.
Vantomme, J.D. (1995) Score Following by Temporal Pattern. Computer Music Journal 19(3), pp. 50-59.
Vercoe, B. (1984) The Synthetic Performer in the Context of Live Performance. In Proceedings of the 1984 International Computer Music Conference. San Francisco: Computer Music Association. pp. 199-200.