In "Tempo Curves Considered Harmful" (Desain & Honing, 1991) we gave a critical overview of the representations of time and tempo used in computer music and music cognition research (collectively named Tempo Curves). We argued that these representations -presented independently of the actual material, i.e. the events that `carry' the expression- are too simplistic, mainly because of their lack of structure. Since the article was restricted to identifying the problems and their causes, the time seemed right to work on possible solutions.
We think that music editors and sequencer programs that are commercially available nowadays are in need of better ways to treat musical information in musically and perceptually relevant ways. For example, expressive timing should not be considered a nasty feature of performed music, as it is in multi-track recording techniques where tempo, timing and synchronisation are treated as technical problems. Instead, expressive timing has to be regarded as an integral quality of performed music whereby the performer communicates structural aspects of the music to the listener.
Another motivation of this work is our interest to make "machines to explore" -in this case to built a tool that allows us to study the expressive patterns in a performance in a far more structured and operative way than was available before, and to gain more understanding of precisely how expression is linked to musical structure (that it is linked, we know from a large body of research on this subject, e.g. Clarke, 1987; Palmer, 1989).
In most of the research on music cognition, expression is defined as the deviations of a performance with respect to the score or the notion of a mechanical performance. This numerical material can be analysed and compared over several performances. Also in most current music software this note-to-note tempo or timing deviation description is used, in the form of a separate tempo track (e.g. sequencers), or as a set of interpretation algorithms acting on a score (e.g. Anderson & Kuivila, 1991). However, from a perceptual point of view, there is something awkward about this definition since a listener can perceive and appreciate expression in a performance without knowing the score.
We proposed to define expression in terms of a performance and its structural description. We can then define the expression of a structural unit as the deviations of its parts with respect to the norm set by the unit itself (Desain & Honing, 1992). Using this intrinsic definition, expression can be extracted from the performance data, taking more global measurements as a reference for local ones, ignoring a possible score. As such, the structural description of a piece becomes central, since it establishes the units which will act as a reference, and it determines the sub-units that will act as atomic parts whose internal detail can be ignored. For example, the expressive dynamics of a performed chord can now be defined as the set of deviations of the loudness of the individual notes from the mean loudness of the chord itself. Or, as another example, the expressive tempo of a bar can be defined as the set of deviations of the local tempo of the beats with respect to the global tempo of the bar.

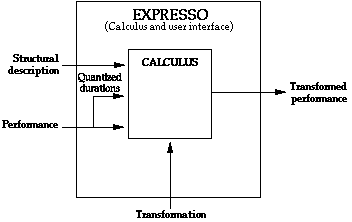
Figure 1. Input/output diagram of Expresso.
The calculus for expression -the heart of the Expresso system- is based on this definition. It is a formalism that allows one to structurally annotate a performance with a set of prototypical temporal structure, and transform specific types of expression with respect to that structural description. A diagram of Expresso is shown in Figure 1. The input consists of a performance and one or more structural descriptions (quantized durations are also needed as input, but they can be derived directly from the performance). The output is a transformed performance. With the Expresso system one can describe and apply transformations in terms of a specific type of expression in a performance (e.g. dynamics) associated with a specific structural unit indicated in the structural description (e.g. the chords), in a way that does not disturb the rest of the expression in the performance.
The next paragraphs describe some aspects of the formalism, skipping most of its detail (see Desain & Honing, 1992 for more details on the calculus).
The underlying representation makes a distinction between basic musical objects and structured musical objects. Basic musical objects are events that `carry' expression (e.g. notes). We assume that their expressive attributes are clearly defined. They should be measurable directly from the performance data, like a note's onset or loudness. The quantized note durations should also be available, for example by quantizing the durations found in the performance. Structured musical objects assign a particular kind of temporal structure to a group or collection of musical objects (possibly a combination of basic and structured objects).
This small set of prototypical structure mirrors some basic distinctions in the perception of temporal structure (see Figure 2), e.g. between successive temporal processes, that deal with events occurring one after another, and simultaneous temporal processes, that handle events occurring around the same time. With respect to expressive timing, events of the first type might use rubato as expressive means- the change of tempo over the sequence. Events of the second type might use `chord-spread' or asynchrony between voices as expressive means, both of a more timbral nature. By assigning a structural type to a collection of musical objects, their behaviour under transformation is uniquely determined. As an example, when a collection of notes is described as a Sequential structure it will be associated with tempo, scaling their timing in an logarithmic way. Their order will be fixed and cannot be changed as a result of a transformation. When the same collection of notes is described as a Parallel structure, they will be associated with asynchrony, scaling their timing in a linear way, allowing their order to be changed.
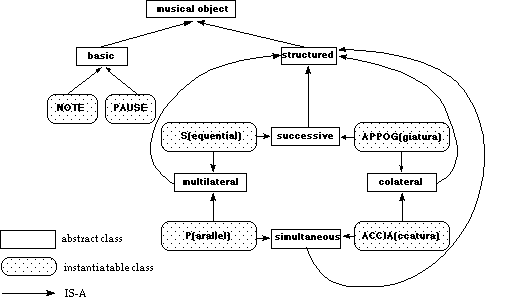
Figure 2. Classes of musical objects and their interrelations.
Unfortunately, expressive parameters in music can not be divided into a small and elegant set of orthogonal types. There is always some kind of interaction between types of expression -one type of expression can not be changed without influencing the other. For example, shifting the onsets of a collection of notes will interact with the expression through the articulation (the offsets of the notes). An important characteristic of Expresso is that it provides some sensible default behaviour, such that changing one type of expression does not destroy all other expressive detail in the performance. An example will illustrate these consistency mechanisms.
Assume we record a performance of a musical fragment with a sequencer. We describe it structurally as a melody and an accompaniment that occur in parallel, of which the melody consists of a sequence of phrases, and the phrases of sequences of notes, and the accompaniment as a sequence of notes (using the two temporal constructs Sequential and Parallel described above). This forms the input to our system.
Suppose we want to do an expressive transformation on the melody of the recorded fragment. For instance a transformation that modifies the onset timing of the phrases (the atomic elements of the melody). The expression of the melody itself will be used as the norm with respect to which the expression of the atomic parts will be modified. The expression of the melody itself will not be changed (in this case the onset of the melody sequence and that of the next musical object), since it is would change the expression linked to higher level structure.
The atomic parts of the melody now have changed onset times as a result of this arbitrary onset timing transformation. This change of expression has to be propagated to the basic musical objects that carry the expression. One way of doing this is to shift all onsets of the elements of each phrase proportionally, but this will destroy all possible internal detail or structure. For instance, the spread or asynchrony within a chord (a parallel construct) should not be altered when changing the tempo (this actually does happen in sequencers when the tempo is changed: the asynchrony between parallel onsets is changed as well). So a propagation of a change in onset timing has to take the internal structural into account: a Sequential structure will be stretched and a Parallel structure will, as a whole, be shifted in time.
But, even when taking this internal structure into account, the original articulation is lost. We need a way of keeping a related type of expression (in this example the offset timing) consistent with the modified expression (here the onset timing). There is, of course, not a single way to do this (e.g. one can keep the overlap the same, the actual duration or the proportion, etc.) but the formalism provides the hooks to add more specific behaviour for these related types of expression.
Finally, now we changed the expression in the melody, we also need ways of keeping it consistent with the accompaniment that occurs in parallel. Since the onsets of the notes in the melody were moved in time, their relation with the notes in the untransformed accompaniment is gone. Here as well, the formalism provides ways of keeping the accompaniment (a sequential structure that runs in parallel with the transformed structural unit) consistent with the changes in the melody. In this example by keeping the onsets in the accompaniment in proportion with the moved onsets in the melody.
Figure 3 shows a transformation on the expressive onset timing of the melody of a recorded performance of a particular musical fragment. The timing of each note of the melody becomes exaggerated with a higher scale factor (tempo on a log-scale because described as Sequential). The x-axes show the performance time (the circles, squares and plus-signs correspond with the notes in the structural description, bottom part Figure 3). The y-axes show the scaling factor (1 is the measured performance, above 1 is exaggerated, below 1 is reduced expressive onset timing). Figure 3a shows the result without keeping parallel onset expression consistent with the change: the accompaniment (lines marked with white squares) is not affected at all. In Figure 3b, the accompaniment is kept consistent with respect to the original performance (the onsets at scale factor 1). Note that note order can change between melody and accompaniment, because of the structural description in two parallel voices. Furthermore, the grace notes (temporal structures of type ACCIAccatura and APPOGgiatura) are not directly transformed -they shift along with their main note. Finally, the chord asynchrony is kept intact and is not affected by the expressive tempo transformation.
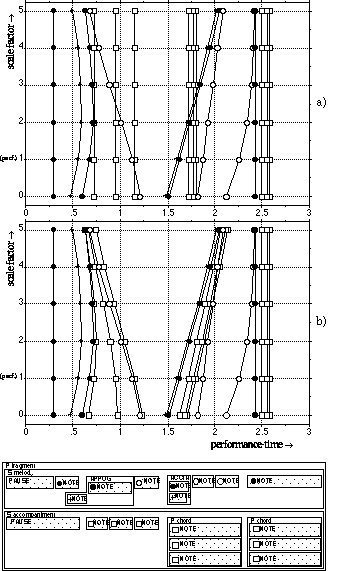
Figure 3. An onset timing transformation on `melody' a) without and b) with "stretching" the accompaniment.
Expresso takes advantage of the object-oriented programming style using the Common Lisp Object System (Steele, 1990). We made extensive use of multiple inheritance (class dependencies that are more complex than simple hierarchies), e.g. in organising the musical objects, their interrelations and associated behaviour (see Figure 2). Multi-methods (functions that are polymorphic in more than one argument) are useful to express transformations in terms of both the type of structure and type of expression. As such, a tempo transformation can be described as an operation specific to the combination of a Sequential structure and onset timing expression. Mix-in type of inheritance (i.e. to group partial behaviour in an abstract class that, mixed in with other classes, supplies that behaviour to their instances) turned out to be an elegant mechanism to model interactions between related types of expression. E.g. an onset timing expression type gets the proper behaviour for offset consistency provided by a `keep-articulation' mix-in (see Figure 4). Method combination (i.e. ways of combining partial descriptions of behaviour of one method for more classes) was especially useful when only certain phases of behaviour are shared among types of expression, and they add their own specific before, after or around behaviour.
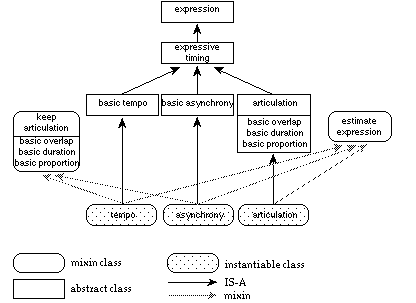
Figure 4. Expression type hierarchy shown for timing related expression.
This paper hopefully shows the importance of introducing an explicit representation of structure in music software. In the Expresso editor described, and the calculus for expression that forms the basis of it, structure plays a central role. A structural description indicates what is the norm and what is considered expressive in a representation of a performance (e.g. a sequencer file), and it can be transformed accordingly. The system provides a small set of prototypical structure and types of expression, together with a number of consistency mechanisms that allow a specific type of expression (associated with a particular structural unit) to be changed without destroying the expression in the rest of the performance.
The knowledge representation provides clear-cut hooks that allows for modification and extension, to introduce new or more specialised knowledge on particular expression types and combinations of musical structure. One could think of adding specific knowledge on the scaling of grace notes under tempo transformations, how a certain scaling of swing should also have its effect on the dynamics of notes and their timbre, or how articulation is dependent on the rhythmical and metrical structure of the piece, etc. Clearly a wide scale of high level descriptions of musical behaviour come to mind, open to immediate test.
Therefore our short term aim is to refine the system into an accessible exploratory tool and further test its musical possibilities. Furthermore, to elaborate on the formalism towards a representational system for music (Honing, in press). We also plan to integrate the calculus into the POCO research workbench (Desain & Honing, 1992).
To conclude, we hope that the Expresso prototype will inspire the development of other music software that can deal with the subtleties of expression in music performance in musically and perceptually relevant ways.
The work presented in this paper was done in collaboration with Peter Desain.
Anderson, D. P. & R. Kuivila (1991) Formula: a programming language for expressive computer music. Computer, July.
Clarke, E. (1987) Levels of structure in the organization of musical time. Contemporary Music Review, 2.
Desain, P. & H. Honing (1991) Tempo curves considered harmful. A critical review of the representation of timing in computer music. In Proceedings of the 1991 International Computer Music Conference. San Francisco: ICMA.
Desain, P. & H. Honing (1992) Music, Mind and Machine, Studies in Computer Music, Music Cognition and Artificial Intelligence. Amsterdam: Thesis Publishers. ISBN 90-5170-149-7.
Honing, H. (1993). A microworld approach to the formalization of musical knowledge. Computers and the Humanities, 27, 41-47.
Palmer, C. (1989) Structural representations of music performance. Proceedings of the Cognitive Science Society. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc.
Steele, G. L. (1990) Common Lisp, the Language. Second edition. Bedford, MA: Digital Press.