Henkjan Honing
[published as: Honing, H. (1995). The vibrato problem: comparing two solutions. Computer Music Journal, 19(3), 32-49. ]
[published as: Honing, H. (1994). The Vibrato Problem. Comparing two ways to describe the interaction between the continuous and discrete components in music representation systems. (Research Report CT-94-14). Amsterdam: Institute for Logic, Language and Computation (ILLC).]
In a number of time-based domains (e.g., animation, music, sound or speech) a distinction can be made between the discrete, symbolic aspects and the continuous, numerical aspects of the underlying representation. In such a `mixed' representation it becomes necessary to describe the interaction between both types of description. This issue of interaction will be discussed by comparing two approaches in the domain of music. In this domain the need for a knowledge representation that can deal with both the discrete and continuous aspects at an abstract and controllable level is charaterized by the vibrato problem. Two formalisms of functions of time that support this notion will be compared: the approach used in the Canon family of computer music composition systems (Dannenberg, McAvinney and Rubine 1986; Dannenberg 1989; Dannenberg, Fraley and Velikonja 1991) and the Desain and Honing (1992a; 1993) Generalized Time Functions (GTF). The comparison is based on a simplified version of the Dannenberg's Arctic, Canon, and Fugue systems (referred to as ACF), obtained from the original programs using an extraction technique, and a simplified version of the GTF system that was made syntactically identical to ACF. In general, both approaches solve the vibrato problem, though in very different ways. The differences will be explained in terms of abstraction, modularity, flexibility, transparency, and extensibility - important issues in the design of a representational system for music (Honing 1993b). The GTF formalism, that was developed for the music domain, is expected to be useful in other time-based representations as well, i.e., representation systems where knowledge about the domain is essential in maintaining isomorphism between the real-world and its representation.
In music representation a distinction can be made between discrete, symbolic representations (like music notation) and continuous, numerical representations (like audio or control signals) (see, e.g., De Poli, Piccialli and Roads 1991). In common music notation, symbolic constructs like, for example, notes, rests, accents or meter can be represented. This notation system, however, lacks appropriate ways of describing the continuous aspects of music (for example, the individual shaping of a note) other than just symbols or words in the score like tremolo or sforzato. By contrast, an audio signal representation allows a "complete" description of a piece of music, with all its continuous aspects. It includes, for example, the sound quality of the instrument, room acoustics, and so on. This type of representation lacks, in turn, symbolic characteristics -we can not (at least not directly) derive the different streams or voices, the beginning of a note, metrical structure, and so on. A similar distinction can be found in computer music systems, with discrete, event-oriented MIDI systems at one end, and continuous signal-oriented systems, like CSound or Music V, at the other. Sometimes one type of representation is more appropriate than the other -a powerful representational system for music needs to integrate both aspects. To give an example, such a system has to allow one to describe how certain parameters change continuously over time, with respect to specific parts or levels of the discrete structure. It has to incorporate specific knowledge on how these parameters change or behave under transformation of that structure (for instance, how a particular kind of phrasing of a rhythmic fragment depends on the duration of that fragment). Consequently, we need to communicate information between the continuous and discrete aspects of a representation, passing information from the discrete components (for example, notes) to the continuous components (for instance, control functions), and vice versa. A relatively simple representational problem characterizing the kind of control that is needed, is the "vibrato problem" (Desain and Honing 1992a).
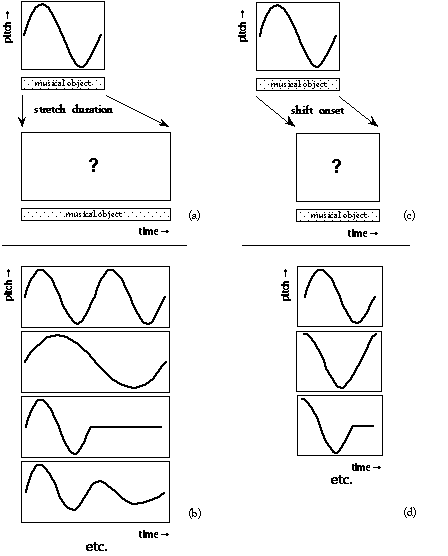
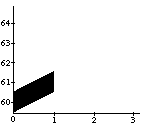
In Figure 1a, a continuous (control) function is used for the pitch attribute of a discrete object -a note. The problem is what should happen to the shape or form of the pitch contour when it is used for a longer note, or, equivalently, when the note is stretched. In the case of its interpretation as an simple sinusoidal vibrato, some extra vibrato cycles should be added to the pitch envelope (see first frame in Figure 1b) -when interpreted as an sinusoidal glissando, the pitch contour should be elasticly stretched (see second frame in Figure 1b). However, all kinds of intermediate and more complex behaviors should be expressible as well (see other examples in Figure 1b). A similar kind of control is needed with respect to the start time of a discrete object (see Figure 1c): what should happen to the contour when it is used for an object at a different point in time, or, equivalently, when the note is shifted? Again a whole range of possible behaviors can be thought of, depending on the interpretation of the control function -i.e., the kind of musical knowledge it embodies (for instance, are they attack-transients, independent or synchronized vibrati, and so on; see Figure 1d).

Figure 1. The vibrato problem. First, what should happen to the form of the contour of a control function when used for a discrete musical object with a different length? For example, a sine wave control function associated with the pitch attribute of a note (a). In (b) possible pitch contours for the stretched note, depending on the interpretation of the original contour, are shown. Second, what should happen to the form of the pitch contour when used for a discrete musical object at a different point in time (c)? In (d) possible pitch contours for the shifted note are shown. There is, in principle, an infinite number of solutions depending on the type of musical knowledge embodied by the control function.
In order to get the desired isomorphism between the representation and the reality of musical sounds, a music representation language needs to support a property that we will call context-sensitive polymorphism: "polymorph" for the fact that the result of an operation (like stretching) depends on its argument type (e.g., a vibrato time function behaves differently under a stretch transformation than a glissando time function), "context-sensitive" because an operation is also dependent on the lexical context it is used. As an example of the latter, interpret the situation in Figure 1c as two notes that occur in parallel with one note starting a bit later than the other. The behavior of this musical object under transformation is now also dependent on whether a particular control function is linked to the object as a whole (i.e., to describe synchronized vibrati; see second frame in Figure 1d), or when it is associated with the individual notes (e.g., an independent vibrato; see first frame in Figure 1d). Specific language constructs are needed to made a destinction between these different behaviors.
(Note that the vibrato problem is in fact a general issue in temporal knowledge representation -an issue not just restricted to music. In animation, for example, we could use similar representation formalisms. Think, for instance, of a scene in which a comic strip character walks from A to B in a particular way. When one wants to use this specific behavior for a walk over a longer distance, should the character make more steps [cf. vibrato] or larger steps, i.e. should it start running [cf. glissando]?).
Dannenberg (1989) describes the "drum roll problem" -the discrete analogy of the vibrato problem-, which in the case of stretching should be extended by adding more hits, instead of slowing down its rate. Several systems are based on this idea: the Arctic system (Dannenberg, McAvinney and Rubine 1986), the Canon score language (Dannenberg 1989), the Fugue composition language (Dannenberg, Fraley and Velikonja 1991), and Fugue's latest incarnation Nyquist (Dannenberg 1993). Although these systems differ in several aspects, they all use a transformation system similar to the one proposed in Arctic. This shared mechanism of Arctic, Canon, and Fugue (cq. Nyquist) will be referred to as the ACF transformation system.
The core of the observations in this study are based on analyzing the behavior of simplified versions of ACF and GTF, extracted from the original code using programming language transformation techniques (see, e.g., Friedman, Wand and Haynes 1992). This technique of extraction (Honing 1993a), making a small program from a larger system, is an attractive alternative to rational reconstruction (see, e.g., Richie and Hanna 1990). We will refer to such a simplified program as micro-version or microworld. It consists of a relatively complete set of essential objects and mechanisms, and at the same time it is small and easy to comprehend.
First, we will describe the set of musical objects, time functions and their transformation that is shared by the ACF and GTF micro-versions (see Appendices). Both micro-versions use the Canon syntax (Dannenberg 1989). Sometimes the ACF systems differ among each other, this will be indicated when appropriate. The examples will be presented with their graphical output, using the micro-versions given in the Appendices.
In general, both the ACF and GTF systems provide a set of primitive musical objects (in ACF these are referred to as "behaviors"), and ways of combining them into more complex ones. Examples of basic musical objects are note, with parameters for duration, pitch, amplitude and other arbitrary attributes depending on the synthesis method used, and pause, a rest with duration as its only parameter. (Note that pitches are in MIDI numbers, duration in seconds, and amplitude on a 0-1 scale). These basic musical objects can be combined into compound musical objects using the time structuring constructs named seq (for sequential ordering) and sim (for simultaneous or parallel ordering). In Figure 2 some examples are given.
(note 60 1 1) =>
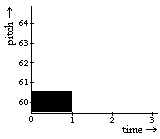
(seq (note 62 1 1)
(pause 1)
(note 61 .5 1)) =>
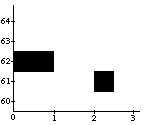
(sim (note 62 1 .2)
(note 61 1 .8)
(note 60 1 .4)) =>
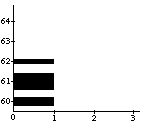
Figure 2. Examples of basic and compound musical objects in ACF and GTF: a note with pitch 60, duration 1, and maximum amplitude (a), a sequence of a note, a rest and another, shorter note (b), and three notes in parallel, each with different pitches and amplitudes (c).
New musical objects can be defined using the standard procedural abstraction (function definition) of Lisp:
;;; define a function
(defun melody ()
;; producing a sequence
;; of three notes
(seq (note 60 .5 1)
(note 61 .5 1)
(note 62 .5 1)))
Figure 3 shows an example of its use.
(seq (melody) (melody)) =>
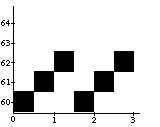
Figure 3. A sequence of twice the same user-defined musical object melody.
Both ACF and GTF provide a set of control functions or functions of time, and ways of combining them into more complex ones. We will use two basic time functions in this article: a linear interpolating ramp and an oscillator generating a sine wave.
(note (ramp 60 61) 1 1) =>
(note (oscillator 61 1 1) 1 1) =>
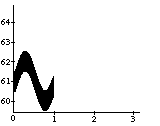
Figure 4. Two examples of note parametrized with basic time functions. A interpolating linear ramp with start and end value as parameters (a), and a sine wave oscillator with offset, modulation frequency and amplitude as parameters (b).
There are alternative ways of passing time functions to musical objects. One method is to pass a function directly as an attribute to, for instance, the pitch parameter of a note (see Figure 4). An alternative method is to make a musical object with simple default values and to obtain the desired result by transformation. In one context the first method might be more appropriate, in another the latter. The following examples show the equivalence between specification by means of transformation and by parametrization (their output is as shown in Figure 4a and 4b, respectively):
;;; specification by transformation (trans (ramp 0 1) (note 60 1 1)) = ;;; specification by parametrization (note (ramp 60 61) 1 1)) (trans (oscillator 0 1 1) (note 61 1 1)) = (note (oscillator 61 1 1) 1 1))
(Note that, while specification by means of transformation is supported in both ACF and GTF, specification by means of parametrization is only available in Arctic and GTF).
Finally, both systems support different types of transformations. As an example of a time transformation, stretch will be used (see Figure 5a). This transformation scales the duration of a musical object (its second parameter) with a factor (its first parameter). As examples of attribute transformations we will use one for pitch (named trans), and one for amplitude (named loud). These transformations take constants (see Figure 5b, 5c and 5d) or time functions (see Figure 5e and 5f) as their first argument, and the object to be transformed as their second argument.
(stretch 2 (melody)) => (trans 2 (loud -0.4 (melody))) =>
 (a)
(a)
 (d)
(d)
(loud -0.4 (melody)) => (trans (ramp 0 2) (note 60 1 1)) =>
 (b)
(b)
 (e)
(e)
(trans 2 (melody)) => (loud (ramp 0 -1) (note 62 1 1)) =>
 (c)
(c)
 (f)
(f)
Figure 5. Examples of transformations on musical objects. A time transformation (a), a constant amplitude transformation (b), a constant pitch transformation (c), a nesting of these two transformations (d), a time-varying pitch transformation (e), and a time-varying amplitude transformation (f).
A central concept in the ACF systems is the notion of a transformation environment. This environment, or context, is implemented as a number of global variables that are dynamically bound and that serve as implicit parameters to every "behavior" (i.e., musical object). Behaviors, transformations and time functions can, in principle, inspect, ignore or modify these variables. They are in fact procedures that know how to change (or "behave") in response to, for example, a stretch or a transpose transformation, and produce continuous signals (e.g., graphical output or MIDI) as a side-effect. The ability of behaviors to adapt themselves -in their own specific way- to changes of the values of these environment variables is the basis of the ACF solution of the vibrato problem: a vibrato behavior will behave differently in an environment modified by, for example, a stretch transformation, than a glissando behavior.
While dynamic binding is a popular programming technique, it often makes a proper understanding of the resulting code very difficult. In order to get a precise insight in how ACF makes use of this technique, we first concentrate on the special variables in the environment that have to do with time, and take a simple note behavior as an example. We will use diagrams to illustrate the specific communication of these implicit parameters and the dynamic binding scheme used. The symbol <- is used for assignment, + for addition, x for multiplication, italics are used for functions, bold face for formal parameters, bold names above a frame indicate an operator or transformation, and curved arrows are used to emphasize references.
There are two implicit parameters in the environment that have to do with time. One holds the current start time (called time in the ACF systems, but it will be referred to as start or S, to distinguish it from actual time or "now"), the other a duration stretch factor (called dur in Arctic and Canon, and stretch in Fugue - we will use stretch or F, to avoid confusion with duration). The global environment is initially set with S (start time) being 0 and F (stretch factor) being 1 (see Figure 6). A note procedure, evaluated in this environment, derives its start time and its stretched duration (i.e., product of the note's formal parameter d, for duration, and F) from these implicit parameters. The body of note (indicated with dots in Figure 6) will refer to these time parameters, and produce output as its side-effect. Note that behaviors return their end time (or logical stop time, as it is referred to in the ACF systems) for use by the time structuring behaviors seq and sim.
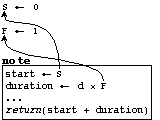
Figure 6. Binding and scope diagram for the expression (note p d). Although note, in reality, has more than two parameters, in these diagrams it is sufficient to look at pitch p and duration d only.
In Figure 7 an example of the seq behavior is shown. It modifies the environment and as a result influences the behavior of note (using dynamic binding). The returned end time, after evaluating the first note, is used to set the value of S. This new value is then used when evaluating the next note, resulting in the notes being ordered (i.e., played or drawn) one after the other.
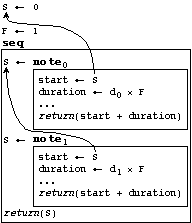
Figure 7. Binding and scope diagram for the expression (seq (note p0 d0) (note p1 d1)), a sequence of two notes.
A sim behavior, conversely, will evaluate all its arguments with the same start time and return the maximum end time (see Figure 8).
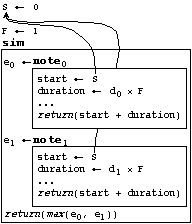
Figure 8. Binding and scope diagram for the expression (sim (note p0 d0) (note p1 d1)), two notes in parallel.
A time transformation in this diagrammatic notation is shown in Figure 9. The stretch transformation alters the duration stretch factor of the enclosing environment by multiplying it with a factor. As a result, the note's duration will be n times as long.
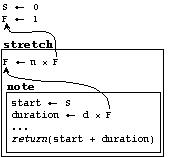
Figure 9. Binding and scope diagram for the expression (stretch n (note p d)), a note made n times as long.
The next example is an attribute transformation (see Figure 10). The trans transformation is used for transposing the pitch of behaviors (if they have such an attribute). The special variable transpose is therefore introduced in the environment (see Figure 10). The note behavior adds the value of transpose to its own explicit pitch (the formal parameter p). For every other transformable attribute (for example, loudness, channel or articulation factor) such a special attribute variable is added to the environment.
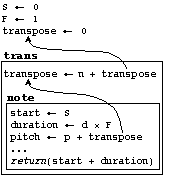
Figure 10. Binding and scope diagram for the expression (trans n (note p d)), a note with a pitch transposed by a constant n.
Finally, the time-varying transformations are shown in the same diagrammatic way for comparison (see Figure 11). In there, an oscillator function is an argument to the trans transformation. Instead of adding a constant value to the value of transpose, a new expression is built from the result of evaluating the oscillator constructor and the value of transpose in the enclosing environment (here 0, but this could be a time function as well). The note procedure body (i.e., the dots in Figure 11) will refer to this "composed" pitch value. (Note that oscillator is actually a time function constructor, that is, it returns a time function. Lambda expressions are used to refer to these anonymous time functions. They are of the form lambda(x1, ..., xn)e, where x1, ..., xn are parameter names and e is some expression).
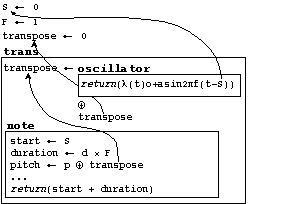
Figure 11. Binding and scope diagram for the expression (trans (oscillator o f a) (note p d)), a note with a pitch transposed by a sine wave time function constructor with parameters offset, modulation frequency and amplitude.
The technique used to make nesting of operations on different attributes possible, and communicate the appropriate values of the environment variables to the behaviors, is dynamic binding. Time functions, behaviors, and transformations can refer to free, but in-visible environment parameters (i.e., not visible at the user-level). It simplifies procedure-call by using implicit parameters communicating information to the behaviors (like start, stretch, transpose and so on), and, therefore, mainly cleans up the syntax (i.e., syntax abstraction). (Note that the transformations in ACF are coded as macro's, not as functions). However, since these environment parameters play a central role in the behavior of the language, the user has to be aware of its workings when using or extending the language, so there is not really abstracted from these implementation details (see Abelson and Sussman 1985).
Furthermore, a particular kind of delayed evaluation is used. Symbolic expressions, describing functions of time, are combined into new expressions that are not yet evaluated. Only at run-time (for example, when the picture is generated) will these expressions be evaluated, and return a fully transformed function of time. This mechanism and the functions of time are made explicit in the ACF microworld using a time function combinator (a circleplus in the diagrams).
Equation 1 shows an example of a time function constructor (oscillator) that returns an anonymous function of time lambda(t). Its behavior is described by an expression that has access to time t, the formal parameters of the oscillator constructor, i.e., o(ffset), f(requency), and a(mplitude), and to start time (S) that is bound to its value in the enclosing environment (cf. Figure 11):
![]() (1)
(1)
The evaluation of, for example, (oscillator 62 1 0.5) will produce a closure that consists of a function of time lambda(t) that has bindings to its three formal parameters (o, f, and a) and to the current (i.e., define time) value of S (Note that S is not a formal parameter).
The approach that was taken in Desain and Honing (1992a; 1993) is that of a mixed representation, i.e., describing those aspects that are best represented numerically by continuous control functions, and those aspects that are best represented symbolically by discrete objects. Together, these discrete musical objects and continuous control functions can form alternating layers of discrete and continuous information. For example, a phrase can be associated with a continuous amplitude function, while consisting of notes associated with their own envelope function, which are in turn divided into small sections each with its specific amplitude behavior. The lowest layer could even be extended all the way down to the level of discrete sound samples.
With respect to the continuous aspects (the vibrato problem), control functions of multiple arguments were proposed, so called "time functions of multiple times" or generalized time functions (GTF). These are functions of the actual time, start time and duration (or variations thereof) that can be linked to a specific attribute of a musical object.
If we ignore for the moment the dependence of time functions on absolute start time, they can be plotted as three-dimensional surfaces: they show a control value for every point in time given a certain time interval (see Figure 12). (Similar plots could be made that show a surface dependent on start time). A specific surface describes the behavior under a specific time transformation (e.g., stretching the discrete object it is linked to). In Figure 12 this surface is shown for a simple sinusoidal vibrato and a sinusoidal glissando. (Note that, in these pictures, the flat triangle-shaped surface of a constant value should be considered undefined. An extension of the GTF micro-version explicitly deals with defining reasonable extrapolations of these functions outside the time interval of the object they are used for, but this is beyond the scope of this paper).
 (a)
(a) (b)
(b)
Figure 12. Two surfaces showing the values for generalized time functions as a function of time and duration (start time is ignored in depiction), in the case of a sinusoidal vibrato adding more periods for longer durations (a), and for a sinusoidal glissando that stretches along with the duration parameter (b).
A vertical slice through such a surface describes the characteristic behavior for a certain time interval: the specific time function for a musical object of a certain duration (see Figure 13).
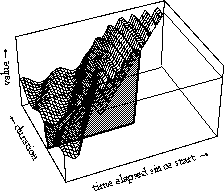
Figure 13. A more complex generalized time function as a function of time and duration (start time is ignored in depiction). The appropriate time function to be used for an object of a certain duration is a vertical slice out of the surface.
Furthermore, there are standard ways of combining basic GTF's into more complex control functions using a set of combinators (compose, concatenate, multiply, add, etc.), or by supplying GTF's as arguments to other GTF's while the components retain their characteristic behavior. Discrete musical objects (like note and pause) also have standard ways of being combined into new ones (e.g., using the time structuring functions S and P -similar to seq and sim in ACF). To integrate these continuous and discrete aspects, the system provides facilities that support different kinds of communication between continuous control functions and discrete musical objects. For example, control functions can be passed to attributes of musical objects either by parametrization (directly pass it to an attribute of, e.g., a note) or by transformation (where the musical objects have default values for their attributes and the desired result is obtained by transformation of the object). Several other paths of communication are supported as well, for instance, passing control functions "laterally" between musical objects (i.e., to have access to the control functions of the preceding or succeeding musical objects in a sequence, e.g., to represent transitions between notes) or a "bottom-up" type of communication where some outer control function is dependent on the behavior of one or more embedded control functions (e.g., when defining an overall amplitude time function that behaves like a compressor). However, we will not discuss these types of communication here (see Desain and Honing 1993 for more details).
Musical object generators (like note, seq or sim) are functions of start time, stretch factor, and an environment. The latter supports a pure functional notion of environment (Henderson 1980), and is in the microworld mainly used to define attribute transformations (see attribute-transform in Appendix C). Other usage is beyond the scope of this paper. Musical object generators can be freely transformed by means of function composition, without actually being calculated (using delayed evaluation). These functions are only in the end applied to a given a start time, stretch factor and environment, and return a data structure describing the musical object that, in turn, can be used as input to a play or draw system. This data structure could take many forms, as long as it contains the start time and duration of the object and it is possible to associate GTF's with attributes of such objects. In the GTF micro-version an ad hoc unstructured event-list representation is used for simplicity -the full system uses a more elegant set of hierarchical musical objects.
Generalized time functions are functions of three arguments, start, duration and actual time (i.e., lambda(s,d,t)). Equation 2 shows an example of an oscillator time function constructor that returns such a function (Note that in the case of oscillator the duration parameter d is ignored).
![]() (2)
(2)
The interpreting system that generates, for example, pictures or prints text (see the output function in Appendix C) will communicate the start time (s) from the object to which attribute the GTF is associated, and samples the resulting time function (i.e., a slice out of the specific GTF space; cf. Figure 13) according to the needs of the output medium.
A micro-version of the GTF system is given in Appendix C. It contains only the objects and mechanisms central to the current discussion. The naming and order of arguments of the top-level functions is adapted such that the user-level syntax is identical to that used in the ACF micro-version in Appendix B.
In the ACF systems, a time function is, as we saw, a function of time that has access to variables representing duration, start, and stretch factor. In the GTF formalism, a time function is a function of multiple arguments -start, duration and actual time. Both formalisms acknowledge the fact that, next to absolute time, both start time and duration are needed to be able to describe appropriate time-varying behavior under time transformation (for example, to be able to distinguish between a glissando and a vibrato). There are, however, some fundamental differences between the two formalisms that are not easily spotted at first sight. To explore them, the syntax of the GTF was made identical to ACF. With this identical syntax, we can port expressions from GTF to ACF and vice versa, and compare the (graphical) output -when identical expressions result in the same graphical output, we know that the systems have the same semantics.
First, let us have a look at an example of a compound musical object (see Figure 14a). It consists of two notes in a sequence separated by a rest. Both notes have an oscillator time function associated with their pitch attribute, a duration of one and one and a half seconds, respectively, and maximum constant amplitude. The pause has a duration of half a second. The expression has identical output in ACF and GTF (see Figure 14a).
(seq (note (oscillator 62 1 .5) 1 1)
(pause .5)
(note (oscillator 62 1 .5) 1.5 1)) =>
 (a)
(a)
(a-musical-object (oscillator 62 1 .5)) =>
 (b)
(b)
(let ((vibrato (oscillator 62 1 .5)))
(seq (note vibrato 1 1)
(pause .5)
(note vibrato 1.5 1))) =>
 (c)
(c)
Figure 14. Musical objects parametrized with time functions as expressions and their graphical output in ACF and GTF. A sequence of two notes separated by a rest and its identical output in both ACF and GTF (a), abstraction from the pitch parameter and its different output in ACF and GTF (b), using local binding for the expression shown in (a) and its output in ACF and GTF (c).
Suppose we want to abstract from this particular expression. We can do this by making a procedure (using function definition) that takes any time function and communicates it to the pitch parameter of the notes, like in the following expression:
; abstract from the pitch parameter
(defun a-musical-object (pitch)
(seq (note pitch 1 1)
(pause .5)
(note pitch 1.5 1)))
When we look at the output of this function applied to the same time function that was used in Figure 14a, we see that its semantics are different in ACF and GTF (see Figure 14b). In ACF, the sine wave extends over the rest, while in GTF the sine wave starts at phase 0 at the beginning of each note. The same thing happens in the closely related expression in Figure 14c that uses a let binding (the let construct being "syntactic sugar" for function application). This specific difference in semantics between ACF and GTF can be explained by having a closer look at the two definitions of an oscillator time function in the two formalisms (the equations are repeated below):
ACF: ![]() (1)
(1)
GTF: ![]() (2)
(2)
This seemingly small difference in implementation has an important effect on the workings of the systems. In the GTF definition of oscillator there are no free variables -the result is dependent of the function's formal parameters only: a pure functional style. This means that time functions can be bound or combined independent of the context that they are actually used. In contrast, the ACF definition of oscillator has a reference to the free variable S (in fact, it can refer to any of the environment variables). Since this variable, in this case start time (S), can be different in different contexts, the expression can give different results in different contexts. This is an imperative style. In ACF, time functions have to be defined in the context where they are actually used: one cannot, for example, abstract from them in one context and use them in another. In a functional language, one would expect the expression shown in Figure 14a to have the same semantics (i.e., graphical output) as the ones shown in Figure 14b and 14c, since it is a property of such a language that a name can only once be associated with a value. This property is called referential transparency. It is considered a severe loss when this property does not hold (Stoy, 1977). For example, we can no longer be certain that f(x) - f(x) is zero. Thus, reasoning about such programs becomes much harder -the whole mechanism of reasoning about these programs (e.g., the lambda calculus) is lost. Sometimes it is worth to drop this property, for example, in a non-deterministic programming style, but to give it up so early, at the fundamentals of what could become a basis for a representational system for music, seems a mistake. (Note that referential transparency is not a property of Lisp itself, since it combines functional with imperative language constructs).
Since the ACF systems, as we saw, lack three central aspects of a functional language -a name is only once associated with a value (referential transparency), functions can be treated as values (first-class objects), and no side effects-, the claim that Arctic, Canon, Fugue and Nyquist are functional languages should be considered inappropriate.
But, of course, independent of these representation language design issues, we sometimes desire the behavior as exhibited by ACF, in the sense that both time functions should refer to the same start time -as if they were linked to the whole object, instead of being linked to individual notes. To do this properly, without conflicting with the referential transparent let in Lisp, we have to introduce a new construct that is syntactically different. The macro with-attached-gtfs is an example of a construct providing such an alternative semantics (see Figure 15, and Appendix C for its definition). It turns the expression in its body into a musical object generator, attaches the time functions mentioned to the start time and duration of the whole object (instead of using the start times and durations of the individual components: the default case), and communicates these "redirected" time functions to the places where they were mentioned in the expression.
; GTF-specific
(with-attached-gtfs ((vibrato (oscillator 62 1 .5)))
(seq (note vibrato 1 1)
(pause .5)
(note vibrato 1.5 1))) =>
Figure 15. Using a GTF-specific language construct to attach a time function to the whole sequence (instead of to each individual note), to obtain the same result as the expression in Figure 14c/ACF.
With the attach-gtf construct (see Appendix C for its definition) the linking a time function's start and duration parameters to musical objects or values is generalized, i.e., time functions can be linked to any musical object, independent time point or time interval. While the latter two situations are supported in ACF, time functions cannot be linked to musical objects. This is a second major difference between the two formalisms (More examples based on this difference will be given below Flexibility).
Before we continue the comparison, as an exercise to the reader, try to decide whether the following two transformations should have a similar or different result in ACF and GTF: A transposition of a note by a declining glissando of a semitone that is then made twice as long, and a transposition of a note with the same declining glissando that was first made twice as long? This means, in Lisp, is
(stretch 2
(trans (ramp 1 0)
(note 63 1 1)))
the same as
(trans (ramp 1 0)
(stretch 2
(note 63 1 1))) ?
The answer will be given at the end of this paragraph. We will first look at a simpler sub-example, shown in Figure 16. In there the pitch of the note is transposed with a descending linear ramp, adding values to the note's constant pitch. Both ACF and GTF produce the same output.
(trans (ramp 1 0) (note 63 1 1)) =>
Figure 16. Transforming the constant pitch of a note of duration one with a linear interpolating ramp, resulting in a glissando that starts at 64 and ends at 63. (Produces identical output in ACF and GTF).
However, when the note is made twice as long, by giving it duration 2, in ACF the shape of the ramp does not change, while in GTF it stretches along with the note's duration, i.e., the pitch of the note still starts at 64 and ends at 63 (see Figure 17).
(trans (ramp 1 0) (note 63 2 1)) =>
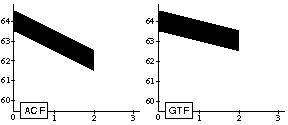
Figure 17. Transforming the constant pitch of a note of duration two with a linear interpolating ramp. (Gives a different result in ACF and GTF).
This is not a bug, but a fundamental language design decision. The difference in behavior is caused by what, again, seems to be a small difference in the two time function definitions. In ACF, at define time a time function lambda(t) is "instantiated." It has access to the formal parameters of ramp and the implicit parameters of the transformation environment (S and F; see Equation 3 shown below). In GTF (see Equation 4), ramp evaluates to a function of start time, duration and time (i.e., lambda(s,d,t)). This definition is independent of the transformations acting on the objects it might be linked to. Note that stretch factor F is not mentioned in Equation 4, while it is in Equation 3.
ACF: ![]() (3)
(3)
GTF: ![]() (4)
(4)
Furthermore, in ACF ramp has an extra parameter named duration (d) that has to be explicitly communicated to the time function, while in GTF, in the default case, the time function is given the duration of the object that it is used for. So, to obtain for this example the same output in ACF as in GTF, ramp has to be explicitly informed about the duration of the object it is used for (duration is underlined):
; ACF-specific (trans (ramp 1 0 2) (note 63 2 1))
All functions of time in the ACF systems have this optional duration parameter (of one second). However, Arctic (Dannenberg, McAvinney and Rubine 1986) elegantly works around this problem by introducing normalized durations -all time functions and behaviors must be explicitly stretched to obtain the desired duration. Another, more elaborate example is shown in Figure 18.
(seq (note (ramp 64 62) 1 1)
(pause .5)
(note (ramp 64 62) 1.5 1)) =>
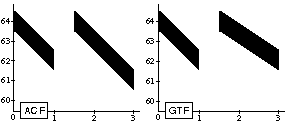
Figure 18. A sequence of two notes with different duration, separated by a rest, each pitch attribute associated with the same ramp time function. (Produces a different output in ACF than in GTF).
Here as well, to obtain the same output in ACF as in GTF, the durations of the individual notes have to be explicitly communicated to every function of time (duration is underlined):
; ACF-specific
(seq (note (ramp 64 62 1) 1 1)
(pause .5)
(note (ramp 64 62 1.5) 1.5 1))
Finally, to come back to our question stated in the beginning of this section with regard to the effect of the order of applying transformations, Figure 19 shows that ACF and GTF give different results -for reasons just described.
(stretch 2 (trans (ramp 1 0) (note 63 1 1))) =>
 (a)
(a)
(trans (ramp 1 0) (stretch 2 (note 63 1 1))) =>
 (b)
(b)
Figure 19. The effect of order of applying a trans and stretch transformation to a note. Stretching a transposed note gives the same result in ACF and GTF (a), transposing a stretched note gives a different result in ACF and GTF (b).
The difference of having time functions that can be attached to musical objects (like in GTF), and time functions that are independent entities and that are sensitive to time transformations as well (like in ACF), indicates an important difference in modularity between the two formalisms. In GTF, time functions and transformations are orthogonal: the definition of one can be changed or extended without influencing the workings of the other. In ACF, time functions and transformations interact (for example, time functions are communicated a stretch factor -a time transformation parameter). The issue of orthogonality will become crucial when the language is extended with, for example, time-varying time transformations (i.e., tempo or event-shift transformations using timing functions) -all behaviors have to be modified to be able to deal with these extensions.
Next, consider the output of the glissando example in Figure 20. For the same reasons as described for the example in Figure 14c, ACF and GTF give different results.
(let ((glissando (ramp 64 63)))
(seq (note glissando 1 1)
(pause .5)
(note glissando 1.5 1))) =>
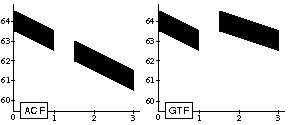
Figure 20. Sequence of two notes with a time function locally bound to the variable glissando, and its differing output in ACF and GTF.
However, the point should be made here that -despite the characteristics of a specific language-, one sometimes wants to express one and sometimes the other behavior, i.e., time functions that are dependent or independent of musical objects. In GTF, the semantics of the ACF example can be obtained by defining a linear ramp that is independent of the duration of the object it is attached to: an independent-ramp (see Figure 21a, and Appendix C for its definition).
But the independent-ramp in GTF is not the same as ramp in ACF. It still uses the start time of the object it is used for. While the time function constructor has a fixed decline/incline, it starts always at the same value at the object's start time (see Figure 21b). This is another behavior that might be preferable in some musical situations.
Yet another alternative is shown in Figure 21c. A ramp is linked here to the whole object, stretching along with its duration, such that it always starts at 64 and ends at 63.
; GTF-specific
(with-attached-gtfs
((glissando (independent-ramp 64 63 1)))
(seq (note glissando 1 1)
(pause .5)
(note glissando 1.5 1))) =>
 (a)
(a)
; GTF-specific
(let ((glissando (independent-ramp 64 63 1)))
(seq (note glissando 1 1)
(pause .5)
(note glissando 1.5 1))) =>
 (b)
(b)
; GTF-specific
(with-attached-gtfs ((glissando (ramp 64 63)))
(seq (note glissando 1 1)
(pause .5)
(note glissando 1.5 1))) =>
 (c)
(c)
Figure 21. Three GTF-specific examples of alternative ways of linking a time function to musical objects. Attaching an linear ramp with its own independent duration (its third argument) to the whole sequence (identical to the output in ACF for the expression shown in Figure 20/ACF) (a), parametrizing the individual notes with a ramp independent of the duration of the object it is used for (it starts at 64 for every note but then has a fixed decline) (b), and attaching a ramp to the whole sequence, resulting in a glissando over the whole object starting at 64 and ending at 63 (c).
The general point here is, that the issue is not about deciding on the correct semantics, but to indicate the amount of flexibility that we need to express a multitude of musical viable situations. Furthermore, the examples above make use of very simple time functions -without mechanisms to compose new time functions from existing ones they will stay trivial examples. It is essential that we can abstract from them, building more musically realistic functions out of simpler ones that are well-understood. As an example, assume we want to define a time function that embodies glissandi with a little vibrato, a simplistic first step in the direction of expressing the musical knowledge used in singing (see Figure 22). We can compose a glissando with a vibrato by adding the results of a ramp that is linked to the whole musical object, and an oscillator time function that is linked to the individual components of the musical object (all this without having to refer to the internal structure of a-musical-object).
; GTF-specific
(defun example ()
(with-attached-gtfs ((glissando (ramp 64 63)))
(let* ((vibrato (oscillator 0 2 .5))
(pitch (time-fun-+ glissando vibrato)))
(a-musical-object pitch))))
(example) =>
 (a)
(a)
(stretch .5 (example)) =>
 (b)
(b)
Figure 22. Output of the user-defined function example that links a composite time function, constructed from a ramp starting at 64 and ending at 63 over the duration of the whole sequence, and an oscillator attached to each individual note (a). It displays the correct behavior when stretched as a whole: the glissando is compressed (but still starts at 64 and end at 63), while the vibrato component drops some periods dependent on the new durations of the individual notes (b).
In ACF, all behaviors and transformations are programs, the output is generated as a side-effect. Functions of time are also, in a sense, behaviors, that can inspect the transformation environment (In Arctic there is indeed no distinction between time functions and behaviors, all behaviors are in fact functions of time). This implicates that if one wants to add a MIDI play function or a graphical extension, all behaviors have to be modified: a tedious job in a full-size system (see Dannenberg, Fraley and Velikonja 1991). In GTF, all objects of the language (musical objects, transformations and time functions) are first-class objects, they deliver data structures and can be bound and passed as arguments. They can therefore be inspected by other programs or serve as input to other systems (for example, a graphical or sound generation system).
This data versus programs distinction also has an important influence on the expressiveness of the representation itself. For instance, in the case of a language with musical objects as procedures, there is no access to these objects after definition. This forces all communication from, for example, time functions to musical objects and vice versa to be realized at define time. Representation problems that can be characterized as based upon "bottom-up" or "lateral" communication, dependent on the accessibility of musical objects after definition, cannot be represented in such languages (see the "compressor problem" and "transition problem" in Desain and Honing 1993).
In this study two formalisms of functions of time were compared, using micro-version programs as a successful means to get an insight in their workings. Although both provide a solution to the vibrato problem, in that they acknowledge the need for more time information besides actual time, several important semantic differences were indicated. These differences were shown to be intrinsic to the design of the two systems and in the way they support of notions like abstraction, flexibility and extensibility.
The article was restricted to the vibrato problem. This problem, of course, reflects just a minor aspect of a representational system for music. Transformations and musical objects -their construction, structuring and use- were left undiscussed. Other, more pragmatic issues, like efficiency and real-time possibilities, were also left untouched. The aim, though, was to achieve a true understanding of what seemed to be irrelevant differences between two relatively simple formalisms. An understanding that is essential, for instance, in deciding for a particular formalism as a fundamental building block of a more elaborate representational system for music. Finally, the vibrato problem is a key example of the kind of expressive power that we need for the next generation of synthesizers that allow high-level, musical control (for example, synthesis methods based on physical models [Smith 1992] or revitalized additive synthesis [Serra and Smith 1990]).
Special thanks to Roger Dannenberg for his open and collaborative attitude, providing full access to his systems; the article benefited greatly from his comments made on earlier versions of this paper. Peter Desain is thanked for helping out at crucial stages of this research and for greatly improving its presentation. Also thanks to Huub van Thienen for his detailed comments on an earlier draft. None of them, of course, necessarily subscribes to any of my conclusions. Remko Scha and the Computational Linguistics Department of the University of Amsterdam should be thanked for providing the environment in which this research could evolve.
Part of this work benefited from a travel grant by Netherlands Organization for Scientific Research (NWO) while visiting CCRMA, Stanford University on kind invitation by Chris Chafe and John Chowning. The research of the author has been made possible by a fellowship of the Royal Netherlands Academy of Arts and Sciences (KNAW).
Abelson, H. and G. Sussman. 1985. Structure and Interpretation of Computer Programs. Cambridge, Massachusetts: MIT Press.
Dannenberg, R. B. (1991a) Fugue Reference Manual. Version 1.0. Pittsburgh: Carnegie Mellon University.
Dannenberg, R. B. (1991b) Review of Time functions function best as functions of multiple times. Unpublished.
Dannenberg, R. B. (1992) Contribution to the computer music composition systems questionnaire. Manuscript. Can be obtained from honing@mars.let.uva.nl.
Dannenberg, R. B. 1989. The Canon Score Language. Computer Music Journal 13(1).
Dannenberg, R. B. 1993. The Implementation of Nyquist, A Sound Synthesis Language. In Proceedings of the 1993 International Computer Music Conference. San Francisco: International Computer Music Association.
Dannenberg, R. B., C. L. Fraley, and P. Velikonja. 1991. Fugue: A Functional Language for Sound Synthesis. IEEE Computer 24(7).
Dannenberg, R. B., P. McAvinney and D. Rubine. 1986. Arctic: A Functional Language for Real-Time Systems. Computer Music Journal 10(4).
De Poli, G., A. Piccialli and C. Roads, eds. 1991. Representations of Musical Signals. Cambridge, Massachusetts: MIT Press.
Desain, P., and H. Honing. 1992a. Time Functions Function Best as Functions of Multiple Times. Computer Music Journal, 16(2). Reprinted in Desain and Honing 1992b.
Desain, P., and H. Honing. 1992b. Music, Mind and Machine, Studies in Computer Music, Music Cognition and Artificial Intelligence. Amsterdam: Thesis Publishers.
Desain, P., and H. Honing. 1993. On Continuous Musical Control of Discrete Musical Objects. In Proceedings of the 1993 International Computer Music Conference. San Francisco: International Computer Music Association.
Friedman, D. P., M. Wand and C. T. Haynes. 1992. Essentials of Programming Languages. Cambridge, Massachusetts: MIT Press.
Henderson, P. 1980. Functional Programming. Application and Implementation. London: Prentice-Hall.
Honing, H. 1993a. A Microworld Approach to the Formalization of Musical Knowledge. Computers and the Humanities, 27.
Honing, H. 1993b. Issues in the Representation of Time and Structure in Music. In Cross, I. and I. Deliège, eds. "Music and the Cognitive Sciences." Contemporary Music Review. London: Harwood Press. Pre-printed in Desain and Honing 1992b.
Michaelson, G. 1989. An Introduction to Functional Programming Through Lambda Calculus. Reading: Addison-Wesley.
Richie, G. D. and F. K. Hanna. 1990. AM: A Case Study in AI Methodology. In Partridge, D. and Y. Wilks, eds. The Foundations of Artificial Intelligence. A Source Book. Cambridge: Cambridge University Press.
Serra, X. and J. O. Smith. 1990. Spectral Modeling Synthesis: A Sound Analysis System Based on a Deterministic plus Stochastic Decomposition. Computer Music Journal 14(4)
Smith, J. O. 1992. Physical Modeling Using Digital Waveguides. Computer Music Journal 16(4)
Stoy, J. E. 1977. Denotational Semantics: The Scott-Strachey Approach to Programming Language Theory. Cambridge, Massachusetts: MIT Press.
The first task in this study was to get a precise understanding of the workings of the Arctic, Canon, and Fugue computer music composition systems. These systems are all well-documented and there are running versions of them available. However, since a full formal specification of these systems is not given, it is not a trivial task to get a grip on the essential mechanisms and objects of these languages.
There are different computer science techniques available that could be used for the analysis of such relatively large programs. A recent technique used in the evaluation of artificial intelligence systems is rational reconstruction (see for instance, Richie & Hanna, 1990). The idea, here, is to reproduce the essence of a program's significant behavior with another program, that is constructed from descriptions of the important aspects of the original program. This evaluation technique was used in studying the Arctic system, taking Dannenberg, McAvinney & Rubine (1986) and Dannenberg (1991b) as the main sources of information. However, the core of the observations in this study are based on a micro-version of the ACF transformation system, extracted from the original code.
The technique of micronization or extraction, making a micro-version program from a larger system, is an attractive alternative to rational reconstruction. Such a micro-version or microworld is a solid basis for further exploration. It consists of a relatively complete set of essential objects and mechanisms and is small at the same time, easy to comprehend, and changes can be made with little effort (Honing, 1993a). It has proven to be a useful technique in the understanding and evaluation of computational models of music cognition (Desain & Honing, 1992b). With respect to this study, micro-versions of Arctic, Canon and Fugue were made, that were tested on a set of characteristic examples of which the semantics were known (i.e., described in the documents mentioned above). These formed a sound basis for distinguishing between syntactic and possible semantic differences of these systems, using programming language transformation techniques (see, e.g., Friedman, Wand & Haynes, 1992). As a result, a micro-version of the ACF transformation system was derived that incorporates the characteristics of all three systems. This allowed to test the workings of the shared transformation system on a wider set of problems than the ones given in the literature and documentation.
The extraction is based on the original code of the Canon score language witten in Xlisp (Dannenberg (1989). It was almost literary used in the Fugue composition language (in Xlisp on the Next machine) and for the Nyquist system (both in Xlisp on the Next machine).
The central objective of making a micro-version of the original Canon code was to make a distinction between the essential representational constructs and implementation aspects, making the basic objects and mechanisms in that language as clear as possible. A similar path was followed for the Fugue code, guided by additional information in Dannenberg (1991a) and Dannenberg (1992). These versions then formed the basis for all kinds of comparisons and modifications (like changing the programming style, adding and removing abstractions, etc.). The resulting micro-version formed the basis for a "rationally reconstructed" Arctic program, that was adapted such that some aspects, unavailable in Canon or Fugue, could be tested and evaluated as well (for instance, functions as only data type, normalized durations, and function composition). These micro-versions were checked with a set of diagnose examples for desired output. The set of diagnose examples were taken from Dannenberg (1989) and Dannenberg (1991b). The latter describes all the examples given in Desain & Honing (1992a) in Arctic syntax. For each micro-version a reference output file was made that served in the testing of input/output equivalence between different versions. This automatic regression testing allowed to confirm whether the stripped version still supported the full example set and whether the changes that were made where just syntactic. In the end, these versions were merged into one ACF microworld using the Canon syntax (see Appendix B).
In the first phase the 450 lines of Canon code were converted to Common Lisp. All error checking code, global variables for pitch names and dynamic markings, and Adagio I/O (a music file format) were removed. Furthermore, the set of global variables used in the transformation environment, and their associated transformations, were reduced to a small set (i.e., leaving out the attribute variables channel and duty, time variables stop and start, and the extract and time warping transformations). The set of behaviors was reduced to note, pause, and ramp only. The oscillator time function was added. All the Adagio output in the behaviors was replaced by a simple output function writing printing text. Some naming was changed (i.e., time to start, dur to stretch, rest to pause). The resulting code (ca. 200 lines) was checked with the set of diagnose examples for desired output (the output of one diagnose example is given at the end of Appendix B) - the output of the micro-version was compared with the output of the original version and tested on equality .
As an example of this first phase, consider the original definition of a ramp behavior, as shown in Figure 23.
1. (defun ramp (type from to &optional channel step) 2. (prog (stop starttime stoptime slope (dur (eval dur))) 3. (setq stoptime (+ *time* (* dur 100))) 4. (setq starttime *time*) 5. (setq *time* (truncate (max *start* *time*))) 6. (setq stop (truncate (min *stop* (+ *time* (* dur 100))))) 7. (cond (step (setq step (truncate step))) 8. (t (setq step 5))) 9. (setq slope (/ (float (- to from)) (- stoptime starttime))) 10. loop 11. (cond ((> *time* stop) (go finish))) 12. (ctrl type (+ from (* slope (- *time* starttime))) channel) 13. (setq *time* (+ *time* step)) 14. (go loop) 15. finish 16. (setq *time* starttime) 17. (return stop)))
Figure 23. Original definition of ramp in Canon.
This procedure was converted from an imperative style to a more functional style, and was stripped from all non-essential aspects. Instead of iterating over a function that writes control information (see Figure 23, line 10-15), the stripped version of ramp (see Figure 24) uses an output function (taking start time, duration and a function of time as arguments). Furthermore, instead of using a procedural description of time functions, it makes time functions explicit (an anonymous function of time; see Figure 24, line 6-9; cf. Equation 3). Finally, the time functions are written in a form that allows easy comparison with the GTF time functions.
1. (defun ramp-behavior (from to &optional (duration 1)) 2. (let* ((start *start*) 3. (stretched-duration (* *stretch* duration))) 4. (output start 5. stretched-duration 6. #'(lambda(time) 7. (+ from 8. (* (/ (- time start) stretched-duration) 9. (- to from)))))) 10. (+ start stretched-duration)))
Figure 24. Stripped definition of ramp.
The second phase is about indicating which parts of the code contain the essential constructs and which parts can be considered just implementation. The task here is to make the central notions explicit and visible in the code. The original definition of the two transformations trans and trans-abs can serve as an example here (see Figure 25). In these procedures a lot of things happen at the same time - they were separated and made visible in the micro-version.
1. (defmacro trans (x s) 2. `(let ((transpose *transpose*)) 3. (prog2 4. (setq *transpose* (list '+ *transpose* ,x)) 5. ,s 6. (setq *transpose* transpose)))) 7. (defmacro trans-abs (x s) 8. `(let ((transpose *transpose*)) 9. (prog2 10. (setq *transpose* ,x) 11. ,s 12. (setq *transpose* transpose))))
Figure 25. Original definition of trans and trans-abs.
First of all, there are two different ways of making transformations (absolute and relative ones). They were added as abstractions (see Figure 26, line 1-4 and 5-6). In Figure 25, line 4 the list construction "delays" the value of transpose, the let and prog2 construct sets up a binding and resets it after evaluating the score-expression, and it finally returns the value of the score expression (i.e., its end time). In the micro-version the composition of expressions describing a time function associated with an attribute variable (see Figure 25, line 4) is replaced by explicit time functions that can used in simple function composition (time-fun-compose function; see Figure 26, line 3), and the dynamic binding (simulated with global variables) is hidden in a macro (In Common Lisp dynamic binding can be achieved with let and special variables). So, besides distinguishing between implementation aspects -simulating dynamic binding -, and more essential mechanisms (delayed evaluation and function composition), it makes addition of new transformations far easier.
1. (defmacro relative-transform (special-var combinator time-fun score) 2. `(let ((,special-var 3. (time-fun-compose ,combinator ,special-var ,time-fun))) 4. ,score)) 5. (defmacro absolute-transform (special-variable time-fun score) 6. `(let ((,special-variable ,time-fun) ,score))) 7. (defmacro trans (increment score) 8. `(relative-transform *transpose* '+ ,increment ,score)) 9. (defmacro trans-abs (increment score) 10. `(absolute-transform *transpose* ,increment ,score))
Figure 26. Making central notions visible.
Note that all transformations and time structuring primitives of the ACF systems have to be defined as macro's. They are syntactic sugar to hide implementation detail. Being a macro, though, they are not first-class objects in the language: they can not be bound or passed as arguments to other procedures.
Finally, the same I/O-system as the one used in the GTF article (Desain & Honing, 1992a) was attached to the ACF microworld, so that the result of an expression in both microworlds could be compared both numerically and graphically, as such forming the basis for the observations in the main part of this article.
The micro-version of the Generalized Time Functions system is comparable to the microworld published in the appendix to Desain & Honing, 1992a, except that the Canon syntax is used and some facilities have been removed. With regard to the full GTF system (Desain & Honing, 1993) the following aspects have been removed or simplified.
The set of time functions and their combinators were reduced to ramp, oscillator and time-fun-compose. The musical objects are hierarchically structured musical objects in the full microworld, but reduced here to an unstructured flat event-list representation for brevity. The time functions are normally curried - at elaboration time a time functions of three arguments (start, duration, and time) are converted to functions of time only, with start and duration derived from the musical object they are linked to. This optimization is left out in the micro-version. And finally, several constructs that support GTF-specific paths of communication were removed as well (e.g., with-attached-time-funs, with-attribute-time-funs, and so on).
ACF Miroworld in Common LISP:
GTF Miroworld in Common LISP: