Composition can be looked at as the making
of choices. Choices can be made by the composer or by the computer.
In the last case the composer (you!) will have to give the rules to
the computer. One of the possible rules is a random choice from a
fixed set of possibilities. We create such a program, by means of the
so called "choice system" ALEATORIC.
A SHOW module asks a color from ALEATORIC each
time the button is clicked. ALEATORIC, upon being requested some
output, asks the CONSTANT module for a list of possibilities. This
module always return the same list of words. ALEATORIC picks one
randomly and returns it to SHOW which displays the color.
![]()
Note that ALEATORIC does not know anything about colors, it just gives you a word as result.
Now we are going to use ALEATORIC to construct a musical example, creating a melody with pitches chosen randomly from a fixed set of possibilities.
Those of you who know about scales, and like to experiment with
them, can immediately start creating random melodies in major, minor,
or other scales, by selecting a suitable list of possibilities. It is
good to build and name modules that will be used more often.
We also can make random rhythms using a duration chosen by ALEATORIC:
Or combine both principles.
In the last example we combined the two mechanisms of choosing random pitches as well as durations. LOCO supports lots of ways of combining very simple mechanisms into complex ones. We encourage the free experimenting with these combinations. They are so manifold that it is impossible to describe them all, just like describing all possible programs is an infinite task.
In the next example we put a duration order of two elements against a melody line of three elements. Can you figure out what goes on when you listen to it?
We can use loudness to accentuate one of the patterns, if you select an instrument on your synthesiser which is sensitive for loudness.
Or the other:
By making our patch into a module it can be used more easily as a building block.
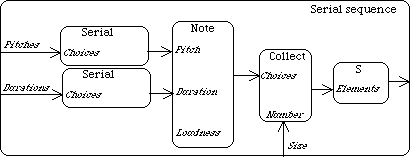
When we use a serial choice for making rhythms, as we did in the second part of the example above, a kind of feeling for measure is created. This happens because after each dotted 1/8 note (1/16 + 1/8 + dotted 1/8) we can be sure a note will start. This even becomes more apparent when a second layer of the same kind of notes is added. This second layer is transposed down by an octave by using the transpose module. This module is one of the general transform modules that can be defined by the user. They operate on any musical object (including compound ones). The definition of these modules is given elsewhere (in the 'composing is transforming musical material' microworld).
Adding a second layer makes the metric quality of the produced sequence even more clear.
Ordered will return the name of an input to select. SELECTED will use that name and asks for it results once (in this example it produces a pitch). NB. the sound example does start with the modules not reset to their starting state.
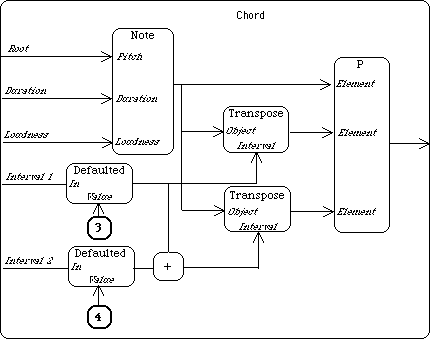
Note how defaults, that will be used when inputs are not connected, are passed to compound modules. A CHORD module is used in the next example, which alternates soft and loud notes with chords.
A whole tone scale has equal steps between every preceding note. You maybe want to compare the sound and making of this scale with the ones you made before with ALEATORIC. Of course, the arguments for SCALE can also be calculated by another choice system.
This example produces a constantly widening serial melody.
The next is an example using SCALE for fluctuating timing of a PRE
grace note attached to a regular beat.
Each pitch is repeated twice. Adding a second layer of double-duration notes, one octave below and without repeating pitches makes a nice combination. The two layers could also be called Balungan and Pekingan, respectively, if it was a first step in making a simulation of a Javanese gamelan styled composition.
The process of doubling musical material in this way would have been expressed more elegantly as a transformation module - but that will be described elsewhere.
Although this is not a very shocking example, CUMULATIVE is a strong principle. It, as its name suggests, cumulates all inputs, beginning with its starting value (c3 in the example above). The next values are determined by the increment. That can be a constant (as in the previous example), but also, and more interestingly, the output of another choice system, as is done the next example, which yields a melody with only thirds as pitch interval steps.
Brown melodies, like the one made here with CUMULATIVE, have a more flowing nature compared to aleatoric (or white) melodies.
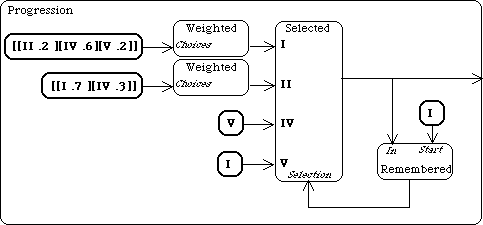
We use this to create a chord progression. Note the use of a textual representation of musical objects, this is not nessecary, but it is sometimes handy to use.
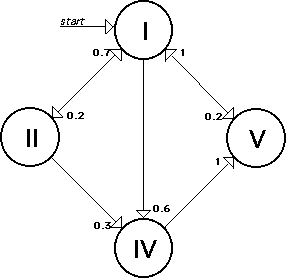
A graphical representation of the chord progression transition network.
COLLECT can be used to aggregate a certain
number of outcomes from a choice system into a list, which can then
be passed as an argument to another choice system. In the next
example 2 pitches are collected in a list which is used 4 times to
derive pitches in order. Thus a number of trills is made.