Make me a Match:
An Evaluation of Different Approaches
to Score-Performance Matching

[Heijink, H., Desain, P., Honing, H., & Windsor, L. (2000). Make me a match: An evaluation of different approaches to score-performance matching. Computer Music Journal, 24(1), 43–56.]

ABSTRACT — A matcher is an algorithm that links events in a musical performance to the corresponding events in a score. Matching is difficult because performers make errors, performers use expressive timing, and scores are frequently underspecified. In this article, two existing matchers are discussed. A general control structrure is described that is used to respecify these matchers, in order to be able to compare them. A new matcher is proposed that uses structural annotations in the score to deal better with the difficulties in matching.

1 Background

Composers of classical music traditionally create musical scores, which musicians translate into performances. A score specifies which notes should be played in what order, and gives information about tempo, loudness, articulation, and structure. The score also contains symbols indicating ornaments like trills, grace notes and glissandi. Whereas information about pitch, note onset, and note duration is unambiguous, information about tempo, loudness, phrasing, articulation, and ornaments is generally not.

Before we explore the relation between scores and performances, we must clarify some terminology. We have to distinguish between a score in musical notation (paper score) and a computational representation of that score (score representation). Similarly, the act of performing music (live performance) will be distinguished from a computationally represented performance (performance representation). In this paper, performances are restricted to MIDI recordings of piano music. In these kinds of performances, the pitch, onset, and duration of every note are clearly defined. We do not consider other aspects of notes, such as timbre or loudness.

Figure 1: The relation between paper scores, live performances, computer representations of scores and computer representations of performances.

The procedure that relates events in a performance to the corresponding events in a score is called matching. A person reading a paper score along with a live performance is matching, but usually the term is reserved for computer programs that are called matchers. Figure 1 summarizes the relation between the concepts mentioned above.

Matchers are used in different contexts for different tasks. One category of algorithms focuses on real-time matching, often called score following (Dannenberg, 1984; Puckette and Lippe, 1992). Another family of algorithms is concerned with non-real-time analyses (Large, 1993; Heijink, 1996; Hoshishiba, Horiguchi, & Fujinaga, 1996), where the quality of the match is more important than efficiency, and the matcher does not have to make decisions in real time.

Accurate matching algorithms are crucial for real-time composition and automatic accompaniment systems. In the context of music performance research, matching algorithms are necessary to be able to measure aspects of a performance like timing: it must be known which performance note relates to which score note to be able to, for example, extract expressive timing patterns and calculate local tempi.

Matching is a complex task for three reasons: performers make errors, performers make use of expressive timing, and scores are frequently underspecified. We will now discuss each of these aspects in turn.

1.1 Performance Errors

Errors are often introduced in the process of transforming the paper score into a live performance. Such errors arise from different sources: notes can be erroneously planned, or properly planned and erroneously executed (Palmer & Van de Sande, 1993). Moreover, if the performer is recorded via a MIDI keyboard, even lightly brushing a key can cause the computer to detect a note, even though the performer did not produce any sound.

A representation for a score and a performance must first be specified to give examples of the different types of errors a matcher encounters. Virtually every matcher uses an approach based on pitch and onset information; this generally yields good results (Hoshishiba et al., 1996; Heijink, Windsor, & Desain, 2000). We will therefore use only this information and see how far it gets us. A score note will be represented as a pair (P, i), where P is the pitch in uppercase letters, and i is the symbolic onset time, a rational number. The onset time is symbolic because a paper score never specifies onset times; it only specifies relative durations. A performance note is represented as a pair (p, t), where p is the pitch in lowercase letters and t is the onset time in seconds.

This notation is used in Figure 2, which shows three different performances of the same score. The performances are on the left, and the scores are on the right. Essentially, there are three kinds of errors: some notes are specified in the score that are omitted (deletion errors) as in Figure 2a, and some notes are played that are not in the score (insertion errors) as in Figure 2b.

Some combinations of insertion and deletion errors can be interpreted as substitution errors, as in Figure 2c, and one of the matchers we discuss in the next section (Large, 1993) is able to make this interpretation. This matcher was used in the context of research into performance errors made by pianists of different levels of expertise (Palmer & Van de Sande, 1993).

If we knew beforehand that there were no errors in the performance, the matching problem would be simplified. However, even expert performers make mistakes. When notes are omitted (deletion error) or added (insertion error), there are often many alternative interpretations of the relation between the performance and the score, especially when the score contains several repeated notes on the same pitch and the performer omits one of them. Extreme use of expressive timing and unexpected interpretations of ornaments may also cause a matcher to misinterpret correct performance events as errors.

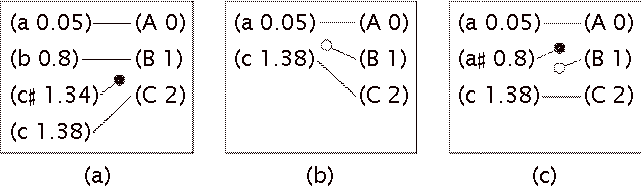
Figure 2: Examples of performance errors: (a) deletion error, (b) insertion error, and (c) substitution error, a combination of an insertion and a deletion error. The symbols used here are explained in the text.

1.2 Expressive Timing

The matchers we discuss in this article use two order constraints. First, notes that should sound simultaneously according to the score can occur in any order in the performance. If, for instance, a score specifies a chord C, E, G, the performance might be C, E, G, in that order, but the performance could also be E, C, G, or G, E, C, due to motor noise, expressive intentions, or recording artifacts. Second, notes in different chords should occur in the order specified in the score. It follows that notes within the same melody cannot be reversed.

Figure 3: An example of voice asynchrony. To distinguish the top voice from the bottom voice, the top voice is in bold face. dashed lines indicate matches that should be made, but are violating the score order.

Most matchers use a very simple concept of note order with regard to scores. A score is represented as a list of notes ordered by onset time and is consequently regarded as a sequence of chords; two notes are in the same chord if they have the same onset; they are in different chords if they have different onsets. However, most paper scores have a different structure, for instance, when there are multiple parallel voices. Some performance notes can occur in a different order than specified in a score representation, e.g., when voices are played out of phase from each other as a result of using extreme expressive timing.

As an example, consider the score and performance in Figure 3. The score specifies that notes (D5 2) and (A4 2) should be played at the same time, and both before note (A4 3). Note that two notes that should be played simultaneously according to the score can reverse order in the performance.

In this case, the performer apparently let the two voices go out of phase, such that note (d5 3.6) is actually played after note (a4 3.5). A matcher is now unable to match (d5 3.6) to (D5 2) without violating the order of the score. We will return to this problem in the section entitled The Structure Matcher.

1.3 Underspecification of Scores

There may be events in the score that are not written out completely, for example, certain kinds of ornaments that are often open to different interpretations. A trill, for instance, can start on the main note or on the note a second above that; moreover, the trill may or may not have a suffix. Therefore, it is unclear how many notes will be in the trill, or even what notes will be in the trill.

2 Existing Research

A very straightforward matcher is the strict matcher, part of the POCO environment (Honing, 1990). The name 'strict' is owing to the fact that the order of the notes, as notated in the score, is taken as a strict temporal constraint on the performance. Notes that have different score times are assumed to be performed in that order in the performance, while notes that have identical score times are allowed to occur in any temporal order. The strict matcher makes use of a window of fixed size that slides through the score, and successive notes from the performance are given a chance to match the score notes in this window. The size of the window, a parameter of the algorithm, is measured in number of score clusters. A cluster is either a single note or several notes expected to happen at the same time. For example, the strict matcher reduces the paper score in Figure 4a to a list of notes, ordered by onset time and grouped in clusters, as in Figure 4b.

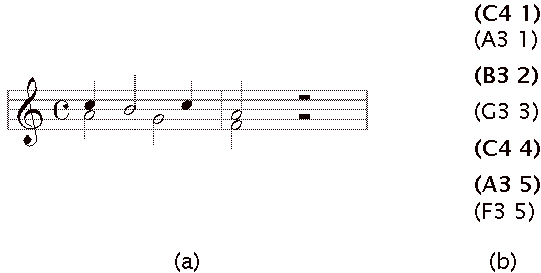
Figure 4: (a) A paper score and (b) the corresponding score representation.

The strict matcher can match two performance notes to two score notes that are in the same score cluster if the onsets of the performance notes differ less than the maximum inter-onset interval (maximum-ioi). It can match two performance notes to two score notes that are in different score clusters if the onsets of the performance notes differ more than the minimum inter-onset interval (minimum-ioi).

The window is advanced through the score when the first cluster in the window contains no more notes that can be matched. This occurs when all the notes in that cluster have been matched, or when a note in a later cluster has been matched, so the score order would be violated if another note in the first cluster would be matched.

The values of the window-size, maximum-ioi, and minimum-ioi parameters are important to the performance of the matcher, because they determine the decision about the type of an error. If the window is too small, the matching score note for a performance note might fall outside the window, causing the performance note to be mistakenly interpreted as an insertion error. On the other hand, if the window is too large, insertion errors might be interpreted as matches instead. Likewise, the minimum-ioi and maximum-ioi parameters can cause misinterpretations of score notes or performance notes.

The strict matcher considers only one possible interpretation of the relationship between score and performance at any point in time, and if an erroneous decision is made, it cannot be corrected later. The strict matcher performs well and efficiently with expert performances, i.e., performances where errors occur only occasionally. However, even in these cases the matcher fails when there is an error in the context of many repeated notes and when parallel voices go out of phase, and the order represented in the score is no longer respected.

Another approach to matching was pioneered by Dannenberg (1984), whose matcher considers many possible alternative matches at any point in time. As an example of this type of matcher, we will discuss a matcher proposed by Large (1993), to which we will refer as the Large matcher. The Large matcher calculates the globally optimal match between a score and performance based on a given 'goodness' function. It treats the score in the same way as the strict matcher, namely, as a sequence of clusters. In contrast to the strict matcher, however, it does not process the performance note by note, but divides the performance into clusters before trying to match it to the score. For this, the matcher uses a maximum-ioi parameter analogously to the strict matcher. The Large matcher interprets some combinations of insertion and deletion as substitution errors; it was used in the context of performance error research, where a classification of errors was important (Palmer & Van de Sande, 1993).

Suppose the score has n clusters and the performance has m clusters. To find the globally optimal match, the Large matcher constructs a table of n rows and m columns, where every cell in the table represents a particular combination of a score cluster and a performance cluster and the whole table represents all possible match alternatives (Large, 1993). The idea behind this procedure is that an optimal match will contain optimal partial matches. The rating at position (i, j) in the table reflects the total goodness of the optimal partial match between the score from cluster i + 1 and the performance from cluster j + 1, augmented with the goodness of the combination of score cluster i and performance cluster j. The goodness measure is determined empirically, and depends upon the character of the performances that are being matched (Large, 1998). After the table has been constructed, the globally optimal match can be read from it. The Large matcher is intrinsically non-real time, since the method uses complete knowledge of the performance and the score to find the globally optimal match. Contrary to the strict matcher, the Large matcher is guaranteed to find this globally optimal match.

When the performance contains few errors, much unnecessary information is calculated. The matcher could be made more efficient by calculating only a band around the diagonal from top-left to bottom-right in the table, instead of computing the entire table: If there were no errors in the performance, the whole match would fall on the diagonal. This approach is used in Dannenberg (1984), where a score window of fixed size was used to limit the size of the diagonal band in the table. When using a window of fixed size, however, it is possible to overlook the globally optimal match, because some information is never considered.

Hoshishiba, Horiguchi and Fujinaga (1996) proposed a matcher that assigns a cost to a transition from one combination of score and performance clusters to another combination. If that transition is made by matching the clusters, the cost is low; if the combination is interpreted as an error, the cost is high. In this way, their matcher constructs a table, where all the cells are connected to their neighboring cells. The best match is then represented as the shortest or cheapest path along the transitions in the table. Like the Large matcher, this matcher calculates too much information if there are few errors in the performance. A similar approach was advocated in Heijink (1996) and an improvement of this approach that solves the efficiency problem was proposed in Desain, Honing and Heijink (1997).

2.1 Summary of Existing Research

We have touched on several matchers briefly and discussed two matchers in detail. The strict matcher and the Large matcher deal in different ways with the three main problems of matching described in the introduction. Both matchers focus on the problem of performance errors, but the Large matcher tends to be more robust in this respect.

With regard to other issues, several authors (Desain & Honing, 1992; Puckette & Lippe, 1992) have acknowledged the problem of expressive timing and its consequences for the behavior of a matcher. So far, no solutions have been proposed.

Indeterminate ornaments are treated only in a matcher proposed by Dannenberg and Mukaino (1988). This matcher is able to handle certain types of trills and glissandi in a simple yet elegant way. However, we would advocate a more general and extendable mechanism to be able to deal with all kinds of ornaments.

Some authors report good results by matching algorithms (Large, 1993; Dannenberg, 1984; Dannenberg & Mukaino, 1988; Grubb & Dannenberg, 1997), but these algorithms are solving a different problem, or are only applicable in certain situations. However, even in evaluations by the authors themselves, some practical matching programs are largely unsuccesful; some researchers even abandon the whole idea of a successful matcher altogether (Puckette & Lippe, 1992).

Experienced human listeners have little or no problem in matching a live performance to a paper score in real time. This is still convincing evidence that robust score-performance matching is feasible, and it inspired us to yet another attempt, based on ideas on mental representation of temporal structure that were developed in the context of studies on expressive timing in music (Desain & Honing, 1992).

3 A Comparison of Different Matching Approaches

Authors of existing matchers describe the way in which their matchers solve a problem, rather than what the solution is. In other words, they describe the implementation of the matchers, rather than the specification (the logical constraints that must hold between score, performance, and matcher) that led to the implementation. Because existing matchers have been implemented in different ways, it is difficult to compare them. For this reason, we have designed a general control structure for matchers, and have specified the strict matcher and the Large matcher in terms of this control structure. We will show that these two matchers are in fact different instances of the same approach. Finally, we will introduce a new matcher that uses structural annotations in the score and show how it can be specified in the same way as the existing matchers.

3.1 A General Control Structure for Matchers

In matching, it is often difficult to decide which note in the score can be matched to a particular performance note. For instance, if the score specifies two consecutive notes with the same pitch, and the performer plays only one of them, that performance note could be matched to either one of the score notes, depending on the situation. An approach that attempts to make a correct decision quickly, like the strict matcher, needs much contextual information. A decision for a present situation may even depend on decisions to be taken later in the process.

The approach we took regarding this problem is similar to the one described in Large (1993). We will allow a matcher to interpret a situation in all possible ways, and postpone the decision about the correct interpretation until all of the alternative interpretations are fully considered.

To clarify this, we must introduce the concept of states. A state contains all the information the matcher needs to make an interpretation of the current situation. At any time during the matching process—that is, in any state—the matcher considers a combination of a particular score note and a particular performance note. Depending on the matcher, it could also consider several notes at the same time. In general, a state contains at least a score cluster and a performance cluster. Both clusters could consist of one or more notes, depending on the situation and the matcher. From a state, the matcher can make transitions to other states. After a transition, the matcher looks at a different place in the performance, at a different place in the score, or both.

All the information the matcher needs is, by definition, contained in a state to prevent the matcher from having to look back at earlier states or transitions. This means that if a matcher needs more information than just the current score and performance cluster—for instance, the strict matcher needs to know the last match made to be able to use the minimum-ioi and maximum-ioi parameters—that information needs to be in the state. We will return to this point after giving an example of the matching process.

Consider a hypothetical matcher that starts at the beginning of the score and the performance and can make three different state transitions at any point. First, it can interpret a state as an insertion error, in which case it skips a note in the performance. Second, it can interpret a state as a deletion error, in which case it skips a note in the score. Third, it can interpret a state as a match, in which case it proceeds by one note in both the score and the performance and stores the match. It can only interpret a state as a match if the pitch of the performance note is equal to the pitch of the score note. The hypothetical matcher tries to match the performance {(a3 1.2), (b3 2.7)} to the score {(A3 1), (B3 2), (B3 3)}.

The matcher interprets every state in three ways and can therefore make two or three transitions, depending on whether a match is possible, so the tree shown in Figure 5 is formed. A state is represented as a node in this tree and is denoted as a performance note followed by a score note in angular brackets. A transition is represented by an edge. The root node is defined as the node without any incoming edges, a terminal node is a node without outgoing edges and an end node is a node representing a state where both the end of the score and the end of the performance have been reached. This means that every end node is a terminal node, but not vice versa.

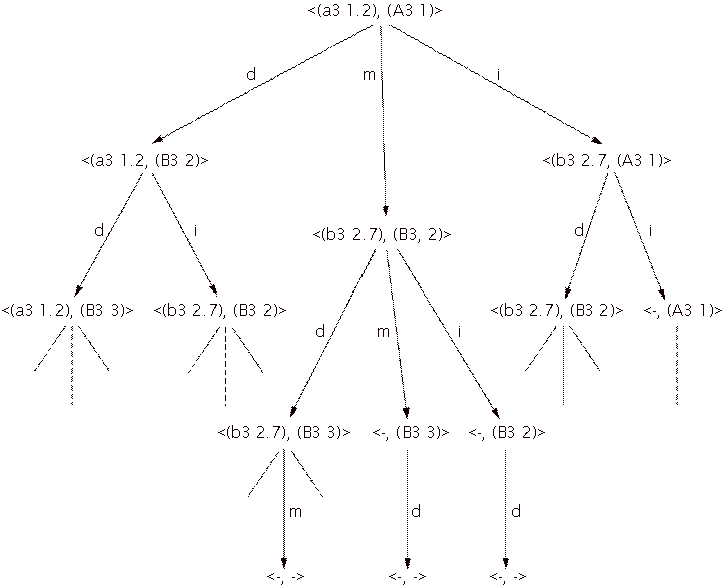
Figure 5: The tree resulting from a match between the performance (a3 1.2), (b3 2.7) and the score (A3 1), (B3 2), (B3 3). The characters next to the edges denote the transitions: m, d and i stand for match, deletion error and insertion error, respectively. A dash instead of a note in the cluster indicates the end of the score or performance is reached.

Every path through the tree from the root node to a terminal node represents a valid match alternative, from which the matcher must choose the best one. The best match alternative is the alternative that contains the most match transitions. The matcher in question determines how this alternative is selected.

Notice that there are some states that are represented more than once in the tree. This means that some alternatives are considered more than once. In the case of large scores and performances this approach is not adequate: the resulting combinatorial explosion must be harnessed before we can speak of a feasible solution. For this we use dynamic programming (Cormen, Leiserson, & Rivest, 1990), noting where two independently developed matching paths arrive again at a same state. Recall that any matcher is required to make its decision about what state transitions to allow on the basis of the information in the current state only. In this case, a state contains only a performance note and a score note. By definition, two different paths ending in the same state will develop in exactly the same way. We can therefore safely combine paths that have common states. The result of this joining of paths in the tree from Figure 5 is the graph in Figure 6. As in the tree of Figure 5, any path through the graph from the root node to a terminal node represents a valid match alternative, from which the matcher has to choose the best one.

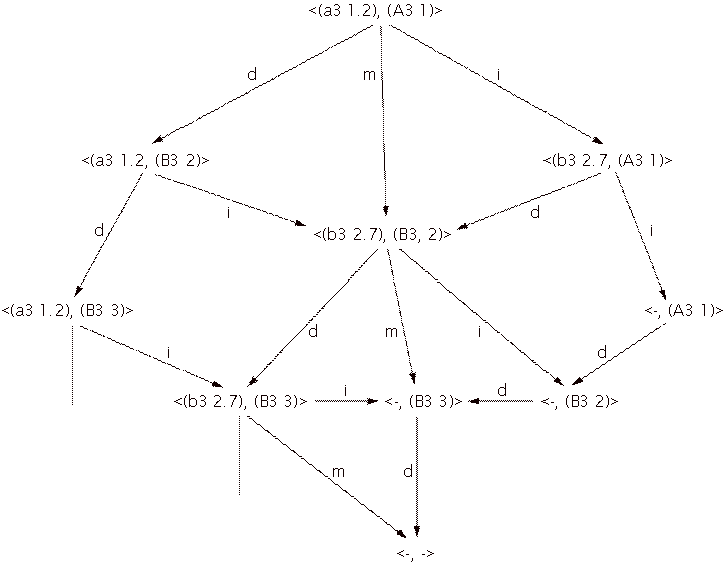
Figure 6: A graph representation of the tree in Figure 5 to prevent representing equal branches more than once.

Although a valuable solution, the use of dynamic programming still yields an enormous data structure for large pieces, and more optimization is required. Fortunately, because expansion of any node in the graph depends only on the contents of the state it represents, the order of expansion is not important, and it is possible to expand the most promising alternative first. For this, a definition of 'most promising alternative' is needed so that each edge or state transition is labeled with a cost; the most promising alternative is defined as the cheapest alternative. The exact cost of each state transition is determined by the rules of the matcher. By expanding nodes in order of their cost the search is structured to obtain a best-first order of path construction in the graph, which prevents the computation of unnecessary information.

The method we outline here is a variant on a standard algorithm for finding the shortest paths from one node to every other node in a directed graph (Dijkstra, 1959). The approach of building a partial graph and selecting the best path in it has already been used by Van der Helm and Leeuwenberg (1991) to account for regularity and symmetry in mental codes for visual perception, and for a model of piano fingering (Parncutt, Sloboda, Clarke, Raekallio, & Desain, 1997) that calculates an optimal fingering pattern among the millions of possible alternatives.

When one path has reached an end node, the cost of that path becomes an upper bound for the cost of other paths. This means that all partial paths with a cost higher than the cost of the first path need not be expanded any further, assuming the cost of a path cannot decrease. However, there could be partial paths with a cost lower than the cost of the first path. If, in expanding the cheaper partial paths, a new one reaches the end node with a lower cost than the first complete path, the upper bound is lowered to the cost of this path. If there are no more partial paths cheaper than this upper bound, all the best match paths have been found.

The mechanism of specifying an upper bound for the cost of a match path maintains its usefulness if more matches must be found than just best matches. If the upper bound is removed after the best paths have been found, the graph building process is resumed until the set of next-best alternatives has been calculated.

The process of building the graph is called phase one. When the relevant part of the graph has been built, generally more than one optimal path exists. Phase two consists of the selection of one path from a potentially large number of best paths. All the paths that are considered in phase two have an equal number of matches, so in the second phase the matcher must use other information such as timing to be able to distinguish the paths. A matcher can use much more information in this phase, because the number of alternatives to compare is much smaller. The strict matcher and the Large matcher do not use timing information, but rather choose a path in the second phase based on the order in which transitions occurred in the first phase. In their original specifications, the second phase was wholly or partly entwined with the first phase. By pulling the two phases apart, it became apparent that these matchers arbitrarily choose a path in the second phase.

3.2 Cost Functions

Cost functions assign costs to transitions. A cost function must satisfy two constraints: First, it should provide a definition of the best match path. We defined this to be the path containing the most matches or, equivalently, the fewest errors. Second, a cost function should assign only non-negative costs to transitions. If the cost of a path could decrease with length, the upper bound provided by the complete path would be meaningless, since a partial path more expensive than the upper bound could become cheaper again later.

An infinite number of cost functions satisfy the constraints, but the exact definition of a cost function has an enormous effect on the size of the graph generated in the first phase. A simple cost function satisfying the above constraints assigns a cost of zero to a match transition and a cost of one to both an insertion and a deletion transition. The cost of a path is then the total number of insertions and deletions in the path.

This simple cost function will assign the same cost to a very short partial match path and a complete match path if they have the same number of errors, which may lead to much unnecessary computation. Ordering the paths with the same number of errors according to their lengths helps in limiting this effect. Moreover, if the score contains more notes than the performance, one needs a minimum number of deletions in the interpretation to be able to reach the end state. A cost function that does not assign a high cost to a deletion in a state in which deletions are still needed is also beneficial for the efficiency of the search. These issues led us to the formulation of cost functions that greatly reduced computation time, but a more elaborate analysis is still needed. Since cost functions only affect the efficiency of the matcher and not the result, we will not discuss them in the rest of this article.

3.3 An Example

We will now give an example of how the hypothetical matcher from the previous section uses a best-first strategy. Going back to the example performance and score of Figure 5, suppose we use a simple cost function that assigns a cost of zero to a match and a cost of one to insertion and deletion errors. The matcher expands the nodes in the graph in a wavelike pattern, starting at the root node (see Figure 7). The waves reflect the order in which the graph is built.

In the following sections, the strict matcher and the Large matcher will be specified in terms of the general control structure. For each matcher, we need to specify a method to proceed through the score and the performance, the amount of information a state should contain, and the permissable state transitions. This determines the first phase of matching: building the graph. For the second phase, we must specify how one match path is selected from the potentially large number of match paths found in phase one.

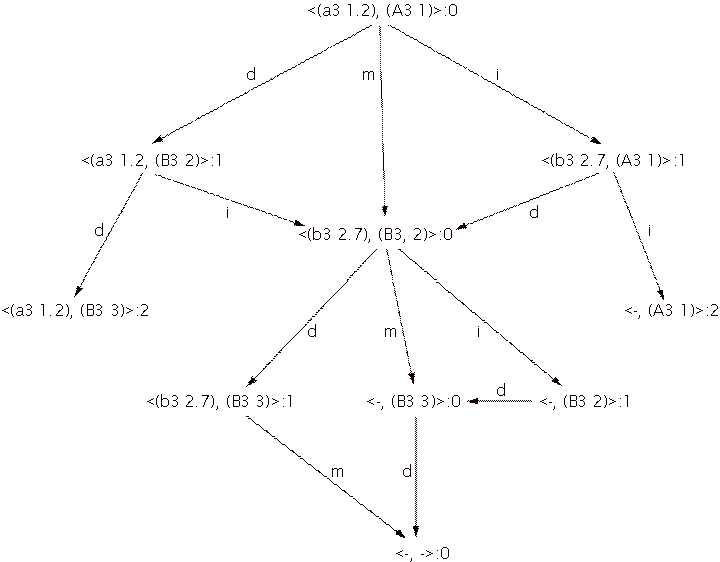
Figure 7: Best-first graph expansion: behind the state is the cost of the node; order of expansion is indicated by the numbered lines.

Because the strict matcher and the Large matcher use different parameters, it is difficult to compare them. For example, should the value of the maximum-ioi parameter be equal for both, or do the matchers react differently to the same value? For this reason, we have chosen to modify them in such a way that no parameters are necessary. We have called the resulting matchers the general strict matcher and the general Large matcher.

The original strict matcher decided whether a state where no notes could be matched was an insertion error or a deletion error, based on the maximum-ioi and minimum-ioi parameters. The general strict matcher does not attempt to decide on a single interpretation of a state, but allows all possible interpretations. It chooses the one containing the greatest number of matches after all the alternatives have been fully investigated, in phase two. Therefore, it does not need the maximum-ioi and minimum-ioi parameters.

The original Large matcher attempted to divide the performance into clusters before matching the performance and the score. The size of the clusters was based on the maximum-ioi parameter. The general Large matcher uses the general control structure to find the optimal clustering of the performance during the matching process itself.

In the original versions of the matchers, there was a distinction between possible paths (only one, in the case of the strict matcher) and impossible paths. The general versions of the strict and Large matchers represent the strength of the general control structure in combination with a cost function: there is no distinction between possible and impossible paths. Instead, every path is more likely or less likely to be the best one.

3.4 The General Strict Matcher

The general strict matcher reads the performance note-by-note and the score cluster-by-cluster. This means that a state contains one performance note and a set of score notes that all have the same onset time. The most important distinction between the original strict matcher and the general strict matcher is that the general strict matcher always considers multiple alternative matches, whereas the original strict matcher always considers exactly one match alternative. Moreover, the original strict matcher poses some constraints on the match that are side effects of the implementation, rather than design considerations. We have lifted these constraints in the general strict matcher.

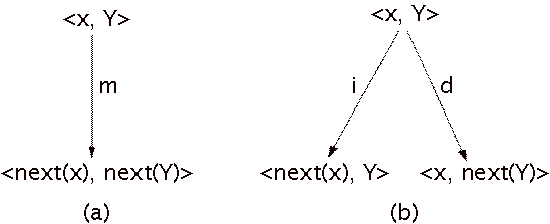
Figure 8: Expansion behavior of the general strict matcher: (a) note x matches (m) with a note in cluster Y, (b) note x does not match any note in the score cluster Y, so this situation is an insertion error (i) or a deletion error (d).

When in a particular state the performance note matches a note in the score cluster, a match is made. If the performance note does not match any note in the score cluster, both a deletion error and an insertion error are considered. This leads to the expansion behavior depicted in Figure 8.

When x matches a note in the score cluster, as in Figure 8a, the next state contains the next performance note and the score cluster without the matched note. If the score cluster contains only one note, the next score cluster is fetched. If there are no matching pitches, as in Figure 8b, both an insertion error and a deletion error are considered.

When the whole graph has been built, several match paths exist. Each of these represents a subset of all possible strict matches between score and performance. In the second phase, the general strict matcher must choose one path from this set: the path that the original strict matcher would choose.

The original strict matcher always matches a performance note when possible. Suppose the matcher is comparing match path A and match path B. It then searches for the first performance note, say p, that is matched in one alternative, but not in the other. If p is matched in A but not in B, the matcher chooses match path A over match path B, and vice versa. In this way the general strict matcher chooses the path the original strict matcher would have chosen from the set of all complete match paths.

3.5 The General Large Matcher

We also have respecified the Large Matcher on top of our general control structure. In the original Large matcher, both the score and the performance are read cluster-by-cluster. Thus, for the general Large matcher, every state contains a performance cluster and a score cluster. A score cluster is a group of notes with equal onset times; a performance cluster is a group of notes such that every consecutive pair of notes has an interonset interval smaller than the maximum-ioi.

In the general Large matcher, this parameter has been eliminated. Instead, we have introduced an extra transition, called cluster enlargement, that adds an extra note to the performance cluster. This transition is applicable in every state, so every score cluster is matched against a performance cluster that grows until it 'fits' the score cluster. The cluster-enlargement transition, in combination with the cost function, automatically finds the optimal clustering of the performance in the course of the matching process.

Another transition is the substitution-error transition. If both the score and the performance cluster contain exactly one note and their pitches are not equal, they are treated as a substitution error.

The expansion behavior is depicted in Figure 9. The Large matcher is always allowed to make an insertion-error or a deletion-error transition, even if two clusters match. If a match is made, the remaining nonmatching notes from the score cluster are considered to be deletion errors and the remaining notes of the performance cluster are considered to be insertion errors.

A cost function for the general Large matcher is more complicated than a cost function for the strict matcher, because the Large matcher has two extra transitions: substitution error and cluster enlargement. A substitution error should be more expensive than a match and less expensive than the combination of an insertion and a deletion error. The cost of a cluster enlargement should be low if the performance cluster contains less notes than the score cluster and high if the performance cluster contains more notes than the score cluster. In this way, a match path where performance clusters are the same size as the corresponding score clusters will be cheapest.

In the second phase, the general Large matcher chooses the best path in the graph in the same way as the general strict matcher. This is not always the same path as the Large matcher would have chosen, but because the choice is arbitrary in both cases, this choice is as good as the other and it makes the matchers easier to compare.

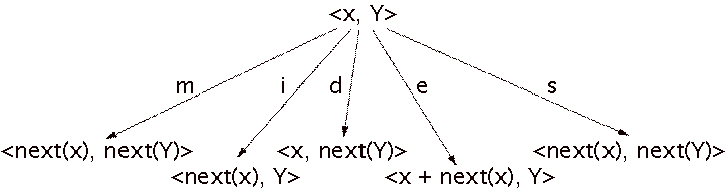
Figure 9: Expansion behavior of the general Large matcher: a match (m), an insertion error (i), a deletion error (d), a substitution error (s) or a performance cluster expansion (e).

3.6 Further Generalizations of the Strict Matcher and the Large Matcher

We have already concluded that there were some idiosyncratic characteristics of the existing matchers that were not apparent in their original specifications. These conclusions could only be drawn from the kind of analyses and respecifications we undertook and inspired us to develop the strict matcher into a general strict matcher and the Large matcher into a general Large matcher, in order to make their behavior more logical and comparable. From the specifications in the previous section, one sees that the general strict matcher and the general Large matcher are in fact very much alike. They have different expansion behaviors and different cost functions, but essentially, they use the same strategy.

If we allow the general strict matcher to interpret a situation where only a match would be possible as an insertion, deletion, or a substitution, the general strict matcher and the general Large matcher can use the same cost function. If the two matchers use the same cost function and the same expansion behavior, they only differ in the way they process the performance and both matchers will ultimately choose the same path. A test of the behavior of these matchers on two Chopin pieces shows that this is indeed the case. The two matchers make the same interpretation of an error in 93 percent of the cases and the differences in interpretation are explained by the substitution-error transition (Heijink, Windsor, & Desain, 2000).

3.7 A Structure Matcher

Neither the general strict matcher, nor the general Large matcher can cope with extreme expressive timing or with ornaments in a satisfactory way. In order to better deal with these problems, we propose another matcher. This matcher, called the structure matcher (Heijink, 1996; Desain, Honing, & Heijink, 1997) is based on the idea that temporal structure annotated in the computer score gives a matcher more clues regarding how to interpret the performance, analogously to structural annotations in a paper score giving a human listener more clues. This is also motivated by the observation that, while expressive timing may greatly upset the order of events as specified in the score, it will mainly do so in ways respecting the musical structure (Desain & Honing, 1992). For instance, notes in a melodic line are not likely to be played in a different order, while parallel voices can be timed independently of each other, so notes in two parallel voices may occur in any order.

If temporal structure (chords, voices, etc.) is annotated in the score, we can predict which order constraints will be observed. These annotations enable us to deal with expressive timing and handle the problem depicted in Figure 3. We will restrict the discussion here to two types of temporal structure, annotated as S (for sequential) and P (for parallel) in the score. A sequential object comprises a number of objects occurring one after the other, for instance, a melody. A parallel object comprises a number of objects occurring at the same time, for instance, a chord, or several voices played at the same time. The score is then a hierarchical structure where the lowest level contains notes and all higher levels contains structural units (S or P).

Most performances cannot easily be divided into clusters, and we therefore decided to have the structure matcher process the performance note-by-note. Processing the score is more difficult due to the structural annotations. For example, consider a case where the score contains several parallel voices. Instead of looking at one score cluster at a time, the structure matcher looks at several score clusters (one for each voice). The matcher can move forward in any voice independently of the others, because each voice can be independently timed.

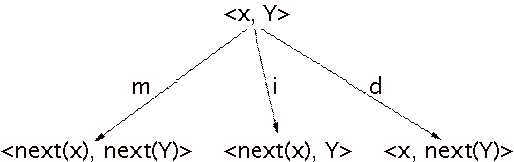
Figure 10: Expansion behavior of the structure matcher: a match (m), an insertion error (i), or a deletion error (d).

The information in a state is limited to a performance note and one score cluster for each voice. The matcher does not require any parameters, and the expansion behavior is kept simple, as Figure 10 shows. Essentially, this expansion behavior is the same as the general Large matcher, except that the performance is processed note-by-note, so the cluster-enlargement transition is not necessary. We decided not to interpret combinations of errors in the first phase, and to exclude the substitution-error transition.

If the score is annotated in such a way that it is a sequence of chords, the only difference between the general strict matcher and the structure matcher is their expansion behavior. (Compare Figures 8 and 10.) If the score is annotated in another way, the structure matcher behaves like an organized set of parallel strict matchers, thereby lifting the restrictions on score structure of the general strict matcher and the general Large matcher.

The behavior of the structure matcher has been compared to the behavior of the other two matchers in matching two Chopin pieces. The results show that the structure matcher performs much better than the other two matchers. When the structure matcher interprets a note as an error, the matcher is right in 85 percent of the cases, while the general strict matcher and the general Large matcher are correct in 42 percent and 46 percent of the cases, respectively (Heijink et al., 2000).

The structure matcher does not make the correct interpretation in all cases, because it only uses pitch and onset information. Moreover, the onset information is only used to establish the order of the notes: actual timing information is not used. In some cases, however, more information is needed to be able to make the correct decision (Heijink et al., 2000).

4 Conclusions

We have discussed several approaches to matching notes in a musical performance to the corresponding notes in the score. Although a simple problem at first sight and an easy task for experienced human listeners, matchers are sometimes not very successful. This is especially true when performance errors occur, when extreme expressive timing is used, or when there are underspecified ornaments in the score.

Such difficulties have led some researchers to abandon matching, or to overestimate the problems involved. Dynamic programming has proved an elegant solution to these difficulties. It allows exploration of multiple alternative matches while keeping the combinatorial explosion of possibilities at bay. This approach has already been proposed by previous authors, but we use it more extensively as a general control structure underneath reimplementations of two different matchers. We also implemented this approach in a new matcher that uses structural annotations in the score.

The general strict matcher, the general Large matcher, and the structure matcher turned out to be very similar. The matchers only differ in expansion behavior and in the use of order constraints, but they are all instances of the same approach. The use of structural information leads to a much better match, as is shown by Heijink et al. (2000).

We believe we have shown that there are insufficient grounds for pessimism with regard to the feasibility of robust score-performance matching. Although not all problems have been solved, robust score-performance matching is feasible if we can more fully exploit the link between the musical knowledge that is expressed or implied in paper scores, and its rendition in musical performances.

5 Future Work

A fundamental object of study is the nature of real performance mistakes (see, for example, Palmer & Van de Sande, 1993) and their interpretation by a matcher. Knowledge of categories of mistakes and how often mistakes in a particular category are made in various situations can be used in the computation, as is done in a simple form by the Large matcher.

The annotations used to indicate sequential or parallel structures for the structure matcher could also be used to specify ornaments, so specialized matchers could be invoked at the appropriate time to deal with these ornaments. The advantage of having specialized matchers is that knowledge of special and complex cases need not be centralized, thereby keeping the algorithm simpler.

The efficiency of the matchers is a problem that is closely related to the problem of finding a good cost function. We have seen that pitch information is often not adequate to distinguish several possible match paths. The use of other information, such as timing information, in the first phase (Vantomme, 1995), rather than in the second phase, would limit the size of the graph, but would also limit the generality of the general control structure.

A practical part of the work will be to make the matchers and related tools available in POCO, and to make POCO directly accessible over the World-Wide Web. Progress on this will be reported on www.nici.kun.nl/mmm.

6 References

Cormen, T. H., Leiserson, C. E., & Rivest, R. L. (1990). Introduction to Algorithms. Cambridge, MA: MIT Press.

Dannenberg, R. (1984). An On-Line Algorithm for Real-Time Accompaniment. In Proceedings of the 1984 International Computer Music Conference (pp. 193–198). San Francisco: ICMA.

Dannenberg, R., & Mukaino, H. (1988). New Techniques for Enhanced Quality of Computer Accompaniment. In Proceedings of the 1988 International Computer Music Conference (pp. 243–249). San Francisco: ICMA.

Desain, P., & Honing, H. (1992). Music, Mind and Machine: Studies in Computer Music, Music Cognition and Artificial Intelligence. Amsterdam: Thesis Publishers.

Desain, P., Honing, H., & Heijink, H. (1997). Robust Score-Performance Matching: Taking Advantage of Structural Information. In Proceedings of the 1997 International Computer Music Conference (pp. 337–340). San Francisco: ICMA.

Dijkstra, E. W. (1959). A Note on Two Problems in Connection with Graphs. Numerische Mathematik, 1, 269–271.

Grubb, L., & Dannenberg, R. (1997). A Stochastic Method of Tracking a Vocal Performer. In Proceedings of the 1997 International Computer Music Conference (pp. 301–308). San Francisco: ICMA.

Heijink, H. (1996). Matching Scores and Performances. Unpublished master's thesis, Nijmegen University, The Netherlands. Available on the World Wide Web at www.nici.kun.nl/mmm.

Heijink, H., Windsor, L., & Desain, P. (2000). Data Processing in Music Performance Research: Using Structural Information to Improve Score-Performance Matching. Behavior Research Methods, Instruments, & Computers, 32(4), 546–554.

Honing, H. (1990). POCO: an Environment for Analyzing, Modifying, and Generating Expression in Music. In Proceedings of the 1990 International Computer Music Conference (pp. 364–368). San Francisco: ICMA.

Hoshishiba, T., Horiguchi, S., & Fujinaga, I. (1996). Study of Expression and Individuality in Music Performance Using Normative Data Derived from MIDI Recordings of Piano Music. In Proceedings of the 4th International Conference on Music Perception and Cognition (pp. 465–470). Montreal: McGill University, Faculty of Music.

Large, E. W. (1993). Dynamic Programming for the Analysis of Serial Behaviors. Behavior Research Methods, Instruments, & Computers 25(2), 238–241.

Palmer, C. &, Van de Sande, C. (1993). Units of Knowledge in Music Performance. Journal of Experimental Psychology: Learning, Memory, & Cognition, 19(2), 457–470.

Parncutt, R., Sloboda, J. A., Clarke, E. F., Raekallio, M., & Desain, P. (1997). An Ergonomic Model of Keyboard Fingering for Melodic Fragments. Music Perception, 14(4), 341–382.

Puckette, M., & Lippe, C. (1992). Score Following in Practice. In Proceedings of the 1992 International Computer Music Conference (pp. 182–185). San Francisco: ICMA .

Van der Helm, P. A., & Leeuwenberg, E. L. J. (1991). Accessibility: a Criterion for Regularity and Hierarchy in Visual Pattern Codes. Journal of Mathematical Psychology, 35, 151–213.

Vantomme, J. D. (1995). Score Following by Temporal Pattern. Computer Music Journal, 19(3), 50–59.