[To be printed as: Timmers, R., Ashley, R., Desain, P., Honing, H., & Windsor, L. (in press). Timing of ornaments in the theme from Beethoven’s Paisiello Variations: Empirical Data and a Model. Music Perception]

Musicians have to make many interpretive decisions when performing a piece. For example, the grace note, a one-note musical ornament, has no precise duration written in the score; it has to steal its duration from either the preceding or following melody notes. There were several empirical questions this study sought to answer: What duration are grace notes given? Does this vary depending upon musical context or individual preferences? And, are their durations taken from the preceding or subsequent melody note, or is time added? In an experiment, 16 professional pianists performed 3 musical fragments (from a Beethoven Theme) ‘with’ and ‘without’ grace notes in 7 different tempi. The timing of the grace notes was found not to be proportional to changes in global tempo for most, but not all performers, which replicates earlier studies. In the majority of cases increases in bar duration were matched by relative increases in grace note duration that were smaller than predicted by a proportional tempo model, with a minority of subjects performing grace notes with fixed duration over tempo. In most cases, grace note duration was ‘stolen’ from the preceding melody note, with a small contribution from the following (main) note, and with minimal disturbance to local tempo. Conversely, where grace notes were played as appoggiatura, the main source of their duration was the main note. The type of grace note performed depended both on its musical context and on individual differences between performers. A model of grace note duration is proposed to account for these results.

Musical ornamentation is the process by which a notated or otherwise canonically specified piece of music is elaborated upon by a performer, largely through the addition of additional note events. Ornamentation not only changes the melodic structure of a piece, but also its rhythmic structure. Such rhythmic modifications may operate by the insertion of extra duration (as in an ornamented fermata) or by occupying some of the duration of neighboring notes without otherwise disturbing the flow of local tempo.
There are a host of questions that arise in connection with ornaments; foremost among these are the interpretation of the figures indicated by various notational conventions (for an overview, see Donington (1989)). Contemporary sources such as the eighteenth-century treatises of C.P.E. Bach (1780), J. Quantz (1752), and F. Geminiani (1749) show considerable disagreement. The same holds for modern scholars. Compare for example Donington (1989) with Neumann (1993). Moreover, all sources fail to offer precise instructions, noting the importance of local and global musical contexts. This is the case even if only one class of ornaments, such as those we now refer to as ‘grace notes’, is taken by itself. Especially in the area of rhythm, where both the time-placement of the ornament and the duration of the ornamental notes may be left largely up to the player’s judgement, a large uncertainty and ambiguity remains. The primary motivation for this study was to determine empirically how particular musical contexts affect the duration of grace notes, and whether such effects of context vary between performers.
A second motivation for this study was the controversial role that grace notes have played in the study of the relationship between expressive timing and global performance tempo. Repp (1994a) has argued that the relational invariance hypothesis (Schmidt, 1985) applies to music as well as it seems to do for many aspects of general motor behavior. He proposed that the duration of a musical event is characterized by its ratio to the duration of the whole, regardless of changes in global tempo. Thus, the durations of individual events scale proportionally: a faster performance will result in a shorter event, maintaining a fixed proportion between the two durations. Repp (1994a) found evidence in support of this: he instructed pianists to perform the same piece ("Traumerei" by Schumann) at different tempi and observed only minor deviations from relational invariance. He concluded that relational invariance holds approximately. However, Desain and Honing (1994) found evidence for non-proportional scaling of timing with tempo in performances of the theme and first variation of the Paisiello Variations by Beethoven. Similarly, the swing rhythm, a typical jazz figure, is not relationally invariant with tempo (Friberg & Sundström, 1999). Most importantly to this paper, and contrary to Repp (1994a), two studies have shown significant deviations from relational invariance in the timing of grace notes at different tempi (Desain & Honing, 1994; Windsor, Desain, Aarts, Heijink, & Timmers, 2001).
This study’s primary concern was to understand the duration and timing of the grace notes within their musical contexts and at different tempi. Secondly, we aimed to gather the necessary data to model the position of a grace note with respect to its surrounding notes and the changes in timing produced when a grace note is inserted. Both aims came with the caveat that different types of grace notes may exist and behave differently. A third aim was to identify these differences and the different musical contexts with which they are associated.
This study sought to improve upon three existing studies of grace note timing (Repp, 1994a; Desain & Honing, 1994; Windsor et al., 2001). Firstly, unlike these precursors, short musical fragments (see filled notes in Figure 1) were recorded in an attempt to minimize effects of tempo drift over the course of a performance (a problem encountered in Windsor et al., 2001). Each performance of the fragments was preceded by a computer-generated performance (see notes with crosses in Figure 1) in order to repeatedly indicate the tempo. This strict tempo control allowed for direct comparison of timing profiles without the need of normalization.


Figure 1. Score of fragments 1, 2 and 3. The annotation indicates boundaries between the introductory bar, the pre bar, target bar and the post bar, and the score times of the melody notes in eighth notes preceding and following the main note. The circled accompaniment note is used as reference note in the grace duration analysis.

Secondly, because each musical fragment was also played without its corresponding grace note, we were able to capture the timing and position of the grace note with respect to this reference. Lastly, the generality of the results across pianists was considered by taking 16 professional pianists as subjects.

Figure 2. The measured melody IOI’s of the ‘without’ (top) and ‘with’ (bottom) condition used in the analysis of grace note timing: ‘without’ previous IOI (a), ‘without’ main IOI (b), ‘with’ previous IOI (a’), ‘with’ main IOI (b’), grace note IOI (c’), ‘without’ bar duration (d), and ‘with’ bar duration (d’).

In the analyses of grace note timing, we made use of four inter-onset-intervals (IOI’s): the previous IOI (a), the main IOI (b), the grace note IOI (c), and the bar IOI (d) (see Figure 2). In reference to these intervals, we distinguished between durations measured in the performance without the grace note as lower case variables (a, b, and d), measured in the performance with the grace note as lower case variables with an accent (a’, b’, c’, and d’), and calculated durations from the score in a mechanical way as upper case variables (A, B, and D). A subscript to the variable indicated the instructed tempo. For example, c’₆₀ means the performed duration of the grace note at tempo 60. Furthermore, we used a non-grace note for reference in the grace duration analyses. For this, we took an eighth note of the accompaniment (see figure 1) and we referred to the duration of this eighth note as e, e’, or E.
Further, we presupposed three prototypical grace note types that are differentiated on the basis of the position of the grace note with respect to the previous note and the main note of the melody (see Figures 2 and 3). The first type is the pre-note grace (Figure 3), which refers to the instances of grace note timing in which the entire grace duration is taken (or stolen) from the previous note. So, local tempo and the duration of the subsequent note (to be called main note hereafter) remain unaffected. The second option is called the on-note grace (Figure 3): the grace note steals its entire duration from the main note. The third type considered is that of the insertion grace (Figure 3). This grace note inserts time: the durations of the previous and subsequent note are unaffected, but time is added, which causes a local slowing of tempo.

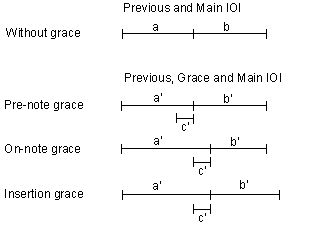
Figure 3. Three types of grace note interpretation: pre-note grace (grace note is performed in time of the previous note), on-note grace (grace note is performed in time of the main note), and insertion grace (grace note does not steal time, but shifts the main note ahead). a is previous IOI; b is main IOI; c’ is grace note IOI.

All stolen times only concern the melody notes. The accompaniment was not taken into consideration. Its position was assumed unaffected by the stealing of time from the previous and main melody note and to shift along with the inserted time.^[1]
We measured the stolen and inserted times by comparing the note durations in the performance with grace note to the note durations in the performance without grace note. Relating the time between the previous onset and the grace note onset to the previous IOI in the ‘without’ condition gave the time stolen from the previous note. Division of this stolen time by the grace note duration defines the proportion of the grace duration that is taken from the previous note (p). This makes comparisons between stolen proportions independent of grace duration that may vary with tempo, grace type and performer.

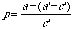
(1)

Note that the comparison is made between a and a’ – c’, since, in the ‘with’ condition, the previous note does not last till the onset of the main note, but till the onset of the grace note.
Direct comparison between the main IOI’s of two performance conditions – the conditions ‘with’ grace note and ‘without’ grace note – defines the proportion of grace duration stolen from the main note (m).

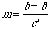
(2)

Finally, inserted time (i) is the time added by the grace note to the total duration between the onsets of the previous note and the next note expressed as proportion of grace duration.

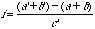
(3)

Note that the three measures p, m, and i are interdependent: they add up to 1. A p of 1 means that the time stolen from the previous note is equal to the grace duration. The other durations can both be zero, or one can be negative and the other positive. Similarly, when m is 1, the entire grace duration is stolen from the main note. And, when i is 1, the time inserted is equal to the grace note duration, or when it is 1/2, half of the grace duration is inserted. A negative p or m means that the notes are lengthened. A negative i means that time is lost: there is less time between the onset of the previous note and the onset of the next note in the ‘with’ condition than in the ‘without’ condition.
The three prototypical ways of grace note performance might be interpreted as referring to different strategies: the pianist prefers not to affect local tempo in a pre-note and on-note grace (i = 0), or prefers not to affect the durations of structural notes in an insertion grace (i = 1). When local tempo is not affected, the duration of the grace note is either stolen from the previous note (p = 1), affecting the previous note offset time (pre-note grace), or from the main note (m = 1), affecting the main note onset time (on-note grace).
The first two types are related to ornament categories as defined in performance practice literature. The on-note grace refers to the class of appoggiatura. The appoggiatura proper is a one note ornament that ‘leans’ on the following, so-called main note (Donington, 2001). It is performed on the beat (m = 1). It is accented and takes half or one third of the time of the main note in case of a long appoggiatura, or less than one third of the time of the main note in case of a short appoggiatura (Donington, 1989; Neumann, 1986).
The pre-note grace refers to a one-note ornament that is performed before the beat (p = 1). According to Neumann (1986), this is a sensible way of performing appoggiatura that precede dotted rhythms in fast tempi, that occur at the start of the piece, before notes of even value, before groups of three even notes, or before staccato notes. Neumann calls this sub-class grace notes. The generality of this last sub-class is debated. For example, according to Donington (1989), there exist only short and long appoggiaturas that occur on the beat. Performance of a grace note before the beat is not considered appropriate, with the only exception of a passing appoggiatura. This passing appoggiatura refers to the special case in which a one-note ornament ‘fills’ a descending third.
The third type (insertion grace) is not mentioned in the literature. Still, we included this as a possibility, since (at least some) time might be inserted when a grace note is added, just as it is possible to lengthen notes or to insert a micro-pause at certain structural positions (see, e.g., Sundberg, Friberg, & Frydén, 1991a).

The prediction was that the grace type interpretation depends on the musical context of the grace note and on the performer’s free or strict interpretation of the rule that appoggiatura are always performed on the beat and no other types of grace notes exist (except the passing appoggiatura that stepwise fills a descending third).
Grace 1 (the grace note of fragment 1) is a descending (but not a passing) appoggiatura: it is a tone above the main note (see top Figure 1) and is followed by three short notes of equal duration. C.P.E. Bach (1780) mentioned this as a context in which the main note cannot be deprived of any part of its value, which could mean that it should be performed as a pre-note grace (as recommended by Neumann 1986) or as an insertion grace, since in both cases no time is stolen from the main note. Donington (1989), in contrast, referred to this context as asking for a short, on the beat interpretation (as our on-note grace).
Grace 2 (the grace note of fragment 2) suspends the previous note and is separated by a melodic leap from the main note (see middle Figure 1). Neumann (1986) referred to this context as a downward leaping appoggiatura. It expresses a feeling of warmth or tenderness and is considered a long appoggiatura, which equals our on-note grace: shortening the main note.
Grace 3 (the grace note of fragment 3) suspends the previous note and is followed by a dotted rhythm (see bottom Figure 1). This dotted rhythm is another instance of a main note that cannot be deprived of any of its value (C.P.E. Bach, 1780). Donington (1989) however made special mention of the suspension, which can only be a true suspension when performed as a long appoggiatura. It is therefore unclear whether one should chose an on-note interpretation to stress the suspension, or an insertion or pre-note grace interpretation in order not to deprive the main note of any of its value.

We also proposed some hypotheses regarding the way in which grace notes are performed at different tempi. On the one hand, one might expect relational invariance, as discussed above. On the other hand, there is some evidence to suggest some considerable deviations from relational invariance in musical performance. For example, it has been suggested that local, small-scale features may keep their characteristic absolute duration, rather than maintaining proportional duration (Repp, 1994a; Desain & Honing, 1994). We inferred from these findings that long appoggiatura that take up half or two third of the main note most probably behave as “normal” notes and keep a constant proportion with the duration of the context. Short grace notes are more likely to maintain absolute, rather than proportional duration. This might be especially likely if an ornament relies upon the insertion of a micro-pause. A finding in language that is in line with this prediction is that the time interval between syllables remains relational invariant with tempo changes, while phonemes keep their duration regardless of tempo (Gentner, 1987).
A different prediction stemming from the performance literature was that grace notes may end up in different categories when performed in different tempi. For example, a long appoggiatura might be most appropriate in a slow and lyrical movement, while short appoggiatura are more natural before rapid notes or in a rapid and playful movement (see Neumann, 1986). Such a change in category might disturb the relational invariance of long grace notes and the constant duration of short grace notes.
To test relational invariance vs. constant duration, we combined the results of two regression analyses. The first provides the slope β and the intercept h of the linear relation between grace note duration c’ and bar duration D (see figure 2). The bar duration was taken as the tempo indicator, since the metrical structure is known as an important contributor in the perception of tempo (e.g., Parncutt, 1994; Clarke 1999).

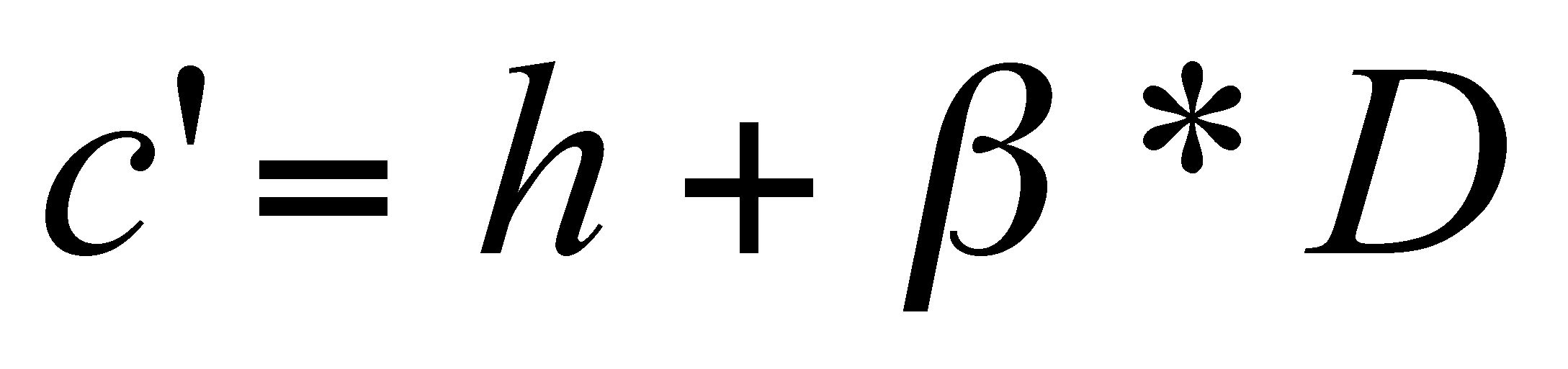
(4)

If the slope (β) is not significantly different from 0, the grace duration does not change with tempo. If it is greater than 0, the grace duration varies positively with tempo.
Following the test of relational invariance in Gentner (1987), the second analysis tests the slope β_prop and the intercept h_prop of the linear relation between grace note proportion and bar duration, where grace note proportion is the ratio between grace duration and bar duration. This analysis tests whether the proportion between grace duration and bar duration remains constant or varies with changes in bar duration. Note that the value at which β indicates proportional scaling is different for different durations of the grace note and therefore this additional test is needed that analyzes the variation in grace note proportion. For conceptual and modeling reasons, it may be more intuitive to speak in terms of a slope s that is 0 for a grace note with a duration that is independent of tempo and 1 for a grace note that scales proportionally with tempo. The slope s can be derived from β using equation 5 (for a further explanation of this derivation see the section “Model”). For statistical purposes, the use of β and β_prop will do.

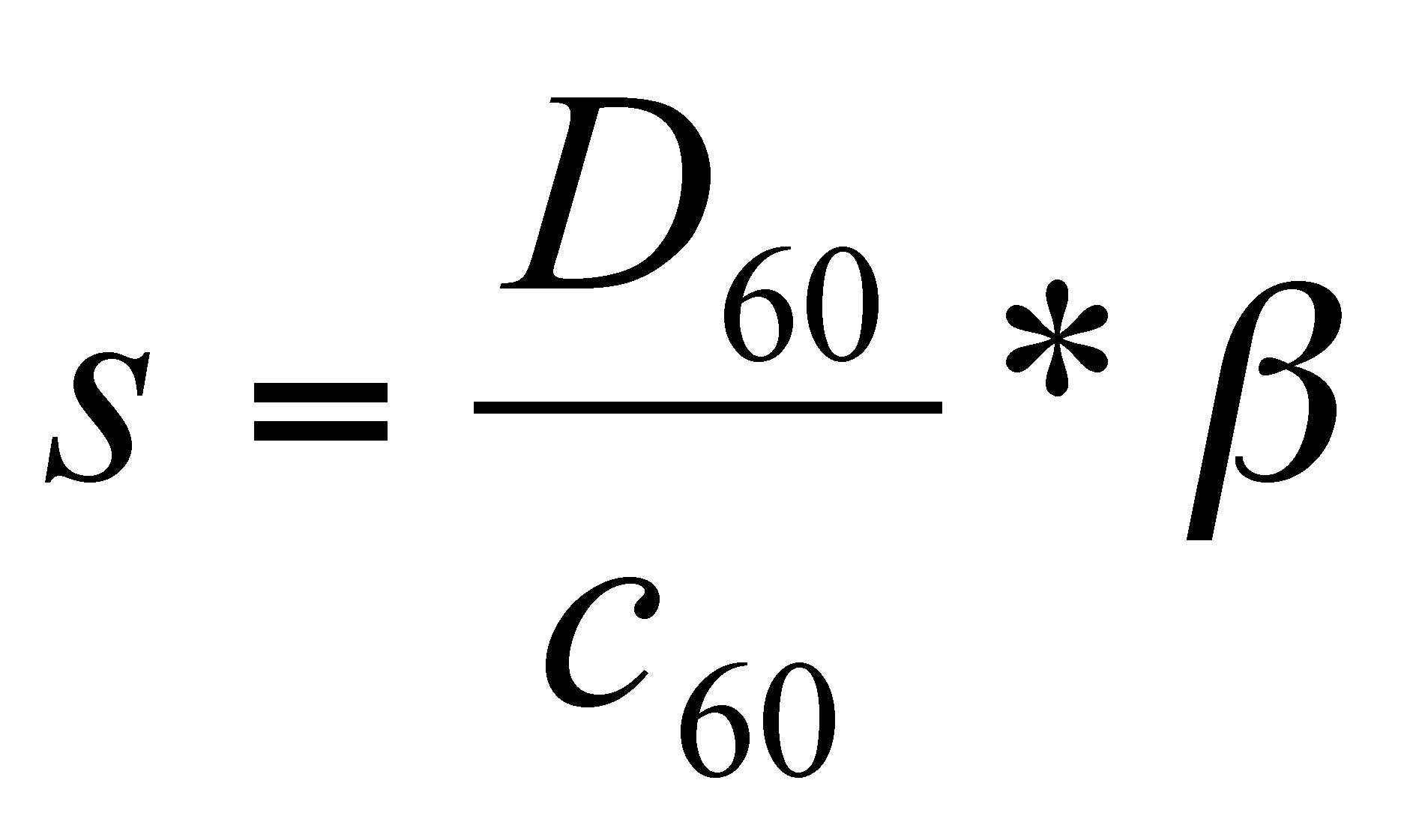
(5)

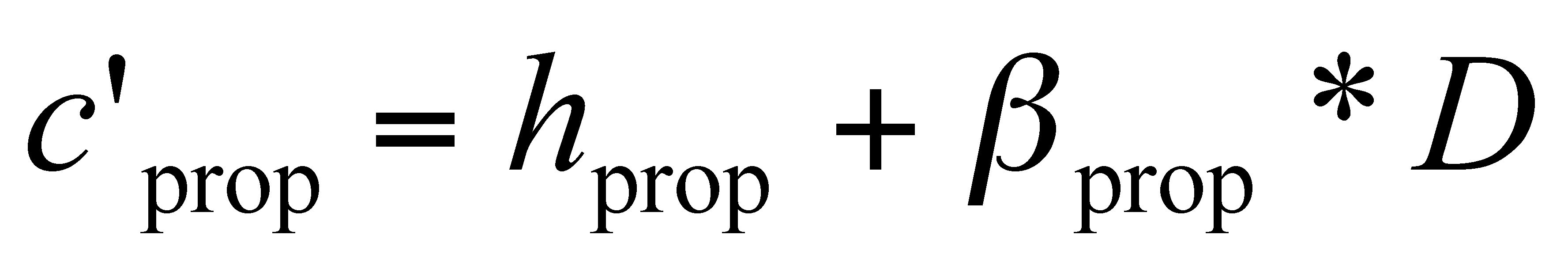
(6)

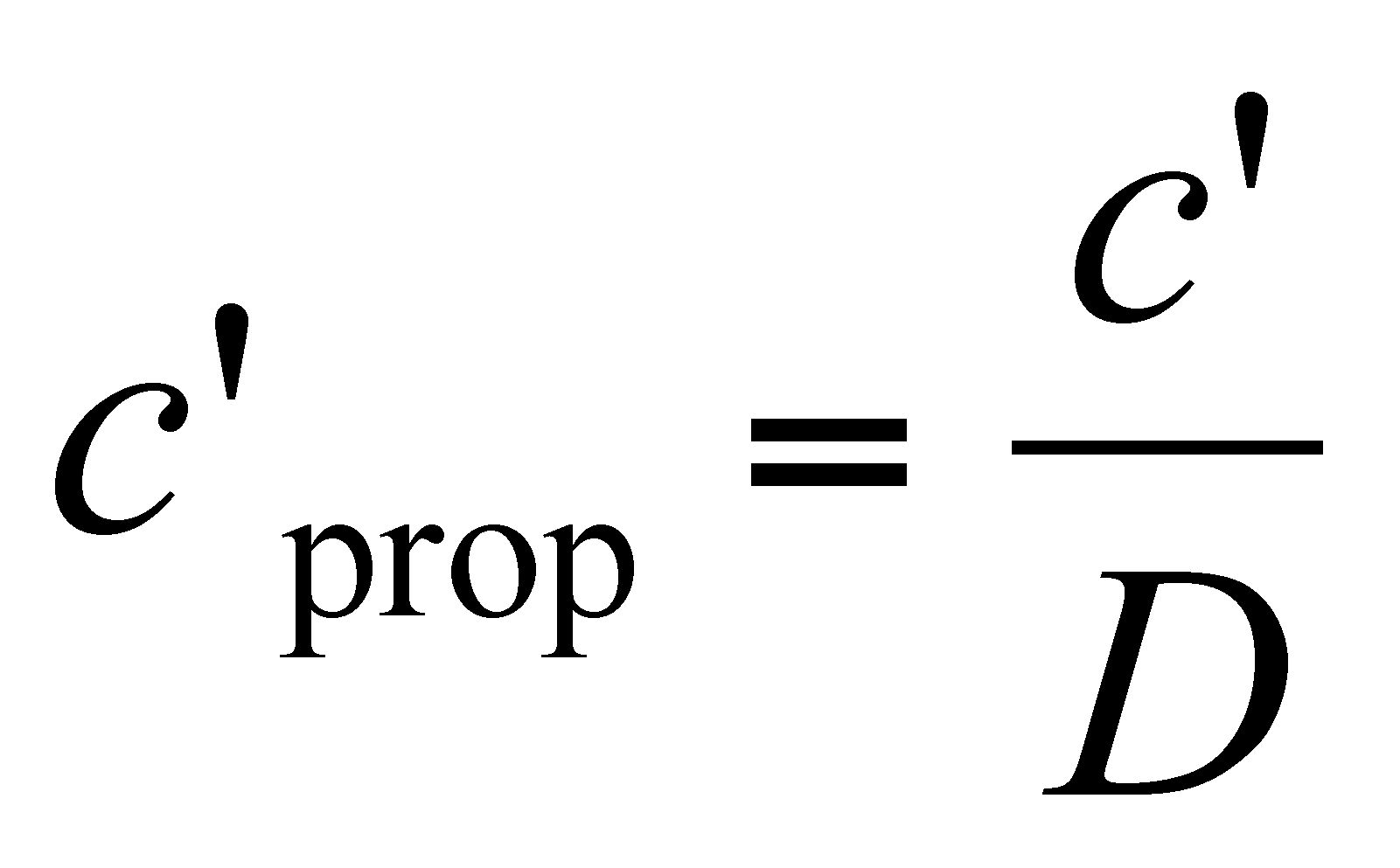
(7)

If the slope (β_prop) of Equation 6 is not significantly different from 0 and β is, the grace note proportion remains constant with varying bar duration, which means that the grace note scales relationally invariant with tempo. If the slope is smaller than 0, the grace note scales less than proportionally with bar duration (the grace note proportion decreases with increasing bar duration). If β_prop is larger than 0, the grace note scales more than proportionally with bar duration (grace proportion increases). As a special case, relational invariance will hold when β is significantly larger than 0, and β_prop is not significantly different from 0. The reason for using two regression analyses is to differentiate between linear and non-linear variations of grace duration with bar duration. If both regression analyses show a slope that is not significantly different from 0, the grace duration does not vary linearly with bar duration.

Three musical fragments were used from the theme of Ludwig von Beethoven's six variations in G-major WoO 70 (1795) on the duet "Nel cor più non mi sento" from the opera "La Molinara" by Giovanni Paisiello.^[2] All fragments contained one measure of introduction, three and a half measures of natural performance and a pause of a length randomly varying between 1/2 and 1 1/2 measures (see Figure 1). The grace note occurs after one and a half measures of the natural performance (see small notes in scores). A metronome indicating the tempo of the 8^th note beats and the half bar precedes each fragment. The endings of fragments 1a and 1c were composed for the purposes of this study by adding the last chord.
These fragments were chosen, because they contain three grace notes that are expected to be timed differently (see section on the predictions concerning grace type and stolen and inserted times). In addition, in a prior study of Windsor et al., (2001), Grace 1 and 3 were played with relatively short IOI’s that varied relationally invariant with context duration, while Grace 2 was performed with significantly longer duration that varied more than relationally invariant with context duration.^[3]

The experiment had three variables: tempo, presence and musical fragment. The tempo variable had seven levels (45, 50, 55, 60, 65, 70, and 75 beats per minute (BPM) with dotted eighth note as beat level). The presence variable had two levels (‘with’ and ‘without’ grace note). And the fragment variable had three levels (the three fragments shown in Figure 1). In addition, each subject repeated each performance in each condition eight times. These repetitions were not considered as a factor in the analyses. Instead, data averaged over repetitions were used.
The order of the tempi was randomized for each subject. The order of the presence conditions was counter-balanced between subjects (see procedure). The order of the three musical fragments was fixed and followed the order of presentation of the original theme.

Sixteen professional pianists participated in the experiment. They were all highly trained pianists with considerable experience in performance and teaching. The Beethoven piece was very familiar to all of them. They used the piece for teaching purposes and had studied it as a student. The pianists were paid for their participation.

The score of the Beethoven theme was sent to the pianists two weeks before the experimental session. The pianists were asked to practice the piece at home in seven different tempi (ranging from 45-75 BPM), both ‘with’ and ‘without’ grace notes.
In the experiment, the pianists did not perform the original Beethoven theme, but were given the six musical stimuli, and asked to play them eight times at each of the seven tempi. Group 1 (subjects 1-8) first performed the fragments 1-3 ‘with’ grace note and then ‘without’ grace note in a certain tempo. The tempo was changed (different order for each subject) and the pianist performed fragments 1-3 again first ‘with’ and then ‘without’ grace note. This continued until all tempi were done. The procedure for group 2 (subjects 9-16) was the same, except that within each tempo block, they performed the fragments ‘without’ grace note before the fragments ‘with’ grace note.
The pianists were instructed to continue to play in the tempo indicated by the metronome and the mechanical introduction, to perform the fragment as musically and expressively as possible, to perform each repeat of a fragment with the same expression and interpretation, not to use any pedaling, and to continue even if they made an error. The recording session was then started and lasted around one and a half hours, including two or three short breaks.
During the recording session, the experimenter kept track of ‘good’ and ‘bad’ repetitions. A repetition was considered ‘bad’ when it contained an obvious mistake (such as forgetting to start performing after the introduction had sounded).

The pianists performed on a Yamaha MIDI grand piano from which MIDI information was sent to a Macintosh G4 running Opcode VISION DSP 4.2.2c. The metronome sound and synthetic piano sound were presented using a Yamaha MU90 synthesizer, while the grand piano MIDI information was recorded. The metronome and intro bar were constructed in POCO (Honing, 1990) as MIDI files. The MIDI recordings were preprocessed in POCO to remove everything except note information. They were then matched to a score allowing for analysis of expressive timing (Heijink, Desain, Honing, & Windsor, 2000).
The resolution of the timing measures was restricted mainly by the MIDI transmission speed (ca. 1 ms), since both the Yamaha MIDI Disklavier and recording software have a resolution finer than this. This means that for the recordings of the Beethoven fragments the timing resolution was between 1-3 ms, because up to 3 notes were performed simultaneously.
Repetitions containing obvious mistakes were left out of the analysis (as mentioned above). Repetitions were also omitted when the grace note, the main note of the melody and the accompaniment or the previous and the next note of the melody were missing.
This process led to the elimination of 1.6% of the total of repetitions across all subjects. Generally, this eliminated one or two of the eight repetitions of each tempo, fragment and grace-note presence condition, with one exception: all performances of fragment 3 by S14 were eliminated for analyses, since in her interpretation, the grace note of fragment 3 substituted the main note. In other words, S14 performed the ‘with’ grace note condition of fragment 3 without a main note. This was seen as too exceptional an interpretation to incorporate in the analyses.

Two checks of tempo adherence were made to ascertain the reliability of the results of the analyses of stolen times and scaling behavior. The first check concerned the consistency of tempo between the ‘with’ and ‘without’ grace note conditions. For this check, we took the pre bar IOI (the first bar performed by the pianists, see Figure 1) as dependent variable, since the start of each fragment must have similar duration in the ‘with’ and ‘without’ conditions. In a repeated measures ANOVA, the effect was tested of tempo category (the computer performed intro bar IOI taken as nominal variable with seven levels), fragment, presence (‘with’ or ‘without’ grace note) and all interactions between them on the pre bar IOI. The effects of tempo category, fragment and the interaction between fragment and tempo category were significant (p < 0.0001). The effects of interest - the effect of presence and the interactions with presence – did not reach significance (p > 0.1), which means that within each instructed tempo category the mean tempo of the pre bar was the same for the ‘with’ and the ‘without’ conditions.
The second check concerned the relation between the intro bar IOI (which equals the duration of a bar in mechanical tempo) and the realized pre bar IOI as plotted in Figure 4. An ideal realization of instructed tempo would predict a perfect proportional relationship (a slope of 1). Instead the relation between realized and intro bar IOI shows a slope of 0.87, which is significantly smaller than 1 (p < 0.0001); there was a tendency for the pianists to perform the higher tempi a bit slower than instructed and the lower tempi a bit faster than instructed.^[4] In other words, the intro bar IOI is not representative for the absolute value of the realized bar IOI. This would be especially harmful in an analysis in which grace duration is related to the intro bar IOI, since it would bias the analysis towards less than relational invariant scaling.

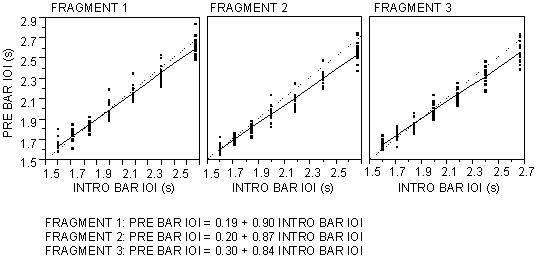
Figure 4. The realized pre bar IOI (the actual duration of the first bar) in relation to instructed bar duration (indicating the tempo at which the pianists were asked to perform). Individual values are shown and the regression line (black). If the pianists were following the instructed bar duration, the black line should be close to the gray line, which indicates a perfect proportional relationship between pre bar IOI and intro bar IOI. Instead, the slope of the black lines for all three fragments is flatter than proportional (smaller than 1).

A solution to this problem was provided by using a measure of realized tempo as independent variable, i.e., a regrouping of the performances into tempo-categories that are in closer agreement with the realized tempi. In this way, the tempo category 45 BPM (reference bar IOI of 2.67 s) only contained performances with a pre bar tempo between 42.5 and 47.5 BPM (pre bar IOI between 2.82 and 2.53 s). The tempo category of 50 BPM only contained performances with pre bar tempi between 47.5 and 52.5 BPM, etc. In other words, the performances were organized in groups of performances with similar pre bar tempi. This organization caused a regrouping of 33%, 39%, and 37% of the performances of fragments 1, 2, and 3, respectively, and .3% to .6% of the performances of the fragments was dropped, since they fell outside of any category. Figure 5 shows that, after this reorganization, the reference bar IOI represents the distribution of realized (pre bar) tempi well – the slope is close to 1 (for fragments 2 and 3, the slope is not significantly different from 1).

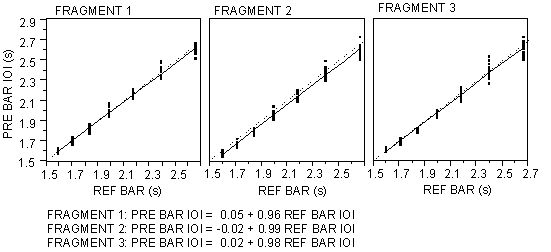
Figure 5. Same as figure 4, only the pre bar IOI’s are presented against their reference bar IOI, which is the instructed category closest to the realized pre bar IOI. The slopes of the line fits are close to 1, which means that the reference bar IOI gives a good indication of the realized tempo.

The question we consider here is how local the effect of the addition of the grace note was: Was the timing of other notes only locally adapted or did more global changes in timing occur as well?
Figure 6 shows that consistent differences between the local tempo patterns of the melody of the ‘with’ and ‘without’ condition only occurred around the grace note, within the target bar, which is indicated by vertical dashed lines. In this figure, the grace note is located between score time –1 (previous note) and 0 (main note, see Figure 1). For Grace 1 and 2, the only difference between the conditions concerned the local tempo of the previous and the main note. For Grace 3, there was hardly any change in local tempo at all.^[5]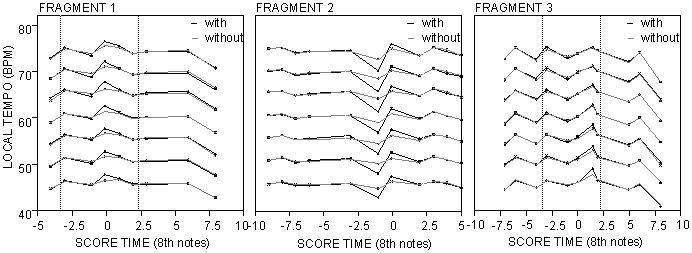

Figure 6. Local tempo per melody note for the three fragments. Separate lines indicate local tempo of ‘with’ (black) and ‘without’ (gray) condition. The melody notes are indicated by score times. Score time 0 refers to the onset of the main note; negative score times indicate the position of a note in eighth notes preceding the main note onset; positive score times indicate the position of a note in eighth notes following the main note onset. The target bar is indicated by vertical dashed lines.

The lack of significant effects of and interactions with grace note presence on the pre bar IOI of the accompaniment as we reported earlier is in agreement with this lack of global effect. However, the same ANOVA with target bar IOI as dependent variable showed a significant interaction between fragments and presence, but no significant main effect of presence. The interaction indicated a generally faster target bar in the ‘with’ condition than in the ‘without’ condition for fragments 1 and 3, but an equally fast target bar in the ‘with’ and ‘without’ condition for fragment 2. Similarly, a repeated measures ANOVA with the post bar IOI of the accompaniment as dependent variable and fragment, tempo category, and presence as independent variables showed no significant main effect of presence, no significant interaction between tempo and presence or between tempo, fragment and presence, but a significant interaction between fragment and presence (p < 0.02). This significant interaction related to a faster post bar in the ‘with’ condition for fragment 2, and to a lesser degree for fragment 1.
We concluded that consistent changes in the onset timing of notes as an effect of the addition of a grace note primarily occurred within the target bar.

The measurements of stolen times and inserted times should provide insight into the position of the grace note and into the adaptation of the duration of surrounding notes to fit in the ornament. To examine the effect of fragment and tempo category on the position of the grace note and the adaptation of the timing of surrounding notes, three repeated measures ANOVA’s were conducted that tested the effect of fragment, tempo category and the interaction between fragment and tempo category on previous stolen proportion, main stolen proportion and insertion proportion, respectively. We conducted separate analyses for each fragment that tested the hypotheses that different grace notes are characterized by either a previous stolen proportion of 1 (pre-note grace), a main stolen proportion of 1 (on-note grace), or an insertion proportion of 1 (insertion grace) with the other proportions being equal to 0.

Relating the time between the previous onset and the grace note onset in the ‘with’ condition to the previous IOI in the ‘without’ condition gives the time stolen from the previous note. Division of the stolen time by the grace note duration gives the proportion of the grace duration (p) that is taken from the previous note (see Equation 1).
The repeated measures ANOVA with p as dependent variable and fragment, tempo category and the interaction between fragment and tempo category as independent variable showed significant main effects of fragment (F (2, 26) =8.73, p < 0.001) and tempo category (F (6, 78) = 3.09, p < 0.01). There was no significant interaction between fragment and tempo category (F (12, 156) = 1.21, p > 0.1). The effect of fragment was such that on average p was larger for Grace 1 and 3 than for Grace 2.
Moreover p did not differ from 1 for Grace 1 and 3 (t (15) = -0.45, p > 0.5 and t (14) = -1.93, p > 0.5 respectively) and was greater than 0 but smaller than 1 for Grace 2 (t (15) = 6.32, p < 0.0001 and t (15) = - 3.03, p < 0.01 respectively).
The effect of tempo category was such that p tended to be smaller for higher tempi (see Figure 7).

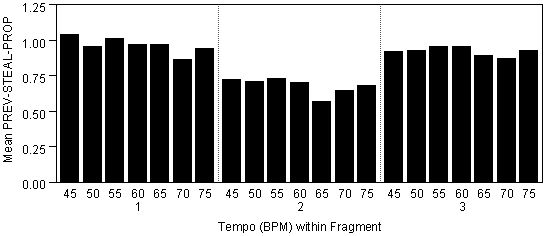
Figure 7. Mean proportion of the grace note duration stolen from the previous note per fragment and per tempo category.

The time stolen from the main IOI is the difference in duration between the main IOI of the ‘without’ and ‘with’ condition. The proportion stolen from the main note (m) is the time stolen from the main note divided by the grace note duration (see Equation 2).
The repeated measures ANOVA with fragment and tempo category as independent variable and m as dependent variable showed no significant main effects of fragment (F (2,26) = 1.39, p > 0.1), tempo category (F (6,78) = 1.74, p > 0.1) and no significant interaction between fragment and tempo category (F (12,156) = 1.35, p > 0.1).
On average, the m was significantly larger than 0 and smaller than 1 (t (15) = 2.94, p < 0.05 and t (15) = -11.55, p < 0.001 respectively). It had a mean of 0.20.

The time inserted is the difference in onset time of the next note with respect to the onset of the previous note between the ‘with’ and the ‘without’ condition. The insertion proportion (i) is the time inserted divided by the grace note duration (see Equation 3).
The repeated measures ANOVA with fragment and tempo category as independent variable and i as dependent variable showed significant main effects of fragment (F (2,26) = 6.85, p < 0.005) and tempo category (F (6,78) =7.95, p < 0.0001) and a significant interaction between these factors (F (12,156) = 6.85, p < 0.005).
The separate analyses for each fragment showed that, for fragment 1, i was significantly smaller than zero (t (15)= -3.49, p < 0.005). For fragments 2 and 3, i was not significantly different from zero (t (15) = 0.065, p > 0.1 and t (14) = 0.27, p > 0.1, respectively).
The interaction with tempo was that for fragment 1, i was negative and approached 0 at faster tempi and, for fragment 2 and 3, i was zero at slower tempi, and positive, though small, at faster tempi (see Figure 8). An explanation for the relative high i at faster tempi is that there is not enough time to insert the grace note.

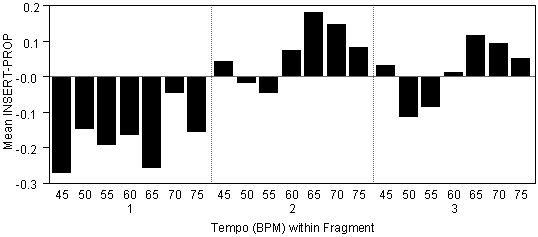
Figure 8. Mean proportion of the grace note duration inserted per fragment and per tempo category.

The next concern was how much the pianists agreed or disagreed in their interpretation of the grace notes.
Table 1 shows for each fragment the number of subjects who timed the grace notes such that no (rows 1 and 2), some (rows 3, 4 and 5) or all time (row 6) is stolen from the main and all (rows 1 and 3), some (rows 2 and 5), or no (rows 5 and 6) time is stolen from the previous note. Mean values for m and p are given per subject group of each fragment. The insertion proportions are not reported, since they are apparent from the other two stolen proportions. The grouping of performances in categories was done on the basis of t-tests that tested the difference of stolen proportions from 0 and from 1.
It can be seen from the data that there were more and different combinations than the three theoretically predicted grace note types. The first category with the most cases agrees fully with the pre-note grace (m = 0 and p =1). The second and third categories partly agree with the definition of the pre-note grace. The fourth category contains instances that lay in between a pre-note and an on-note interpretation (though the instances of this category in Fragment 2 more closely agree with the definition of a pre-note grace than an on-note grace). And the last two categories agree or partly agree with the definition of an on-note grace. The option of the insertion grace is not present in the Table (p = 0 and m = 0): there were no subjects who showed such interpretation. Instead, generally, only a little time was inserted, and the insertion proportion was always much smaller than 1.
It is noteworthy that S14, who interpreted Grace 3 as a substitution of the main note, interpreted both Graces 1 and 2 as an on-note grace. Two other pianists (S1 and S5) changed the interpretation of the graces from a pre-note grace (for Graces 1 and 3) to an on-note grace (for Grace 2).

Table 1. Number of subjects (N) and mean stolen proportions from the previous note (p) and main note (m) for six types of grace note timing and for the three fragments

It is questionable whether the differences between the first four categories and between the last two categories of Table 1 are clearly audible. Most differences in onset times between these categories vary around 15 ms in case of a grace note duration of 60 ms and around 25 ms in case of a grace note duration of 100 ms. The only exceptions to this are the fourth category of fragment 1 and the second category of fragment 2. Those categories show relatively large deviations from the other pre-note interpretations.
The differences between the pre-note (first three categories) and on-note interpretations (last two categories) are undoubtedly perceivable, since the differences in onset timing between the two categories are as large as the grace note duration (which varies between 30 and 160 ms as we will see later). The perturbations also cut at two sides; the difference between a pre-note and an on-note interpretation is that the grace and main note are delayed and the main note is shortened.
Therefore, we interpreted Table 1 as indicating that, generally, all three fragments primarily showed the following pre-note grace interpretation: most to all time stolen from the previous note, little to no time stolen from the main note and no time or negative time inserted. Grace 1 deviated from the prototypical description by showing a negative i and positive m. Both can be attributed to the faster tempo of the target bar in the ‘with’ condition. Both Grace 1 and Grace 2 deviated from the prototypical description by showing “in between” cases. Grace 1 and 2 further showed instances of on-note grace interpretation.
Thus the performance of the grace notes appeared to be only partly determined by the musical context. Specific interpretation by the performer was of equal importance, such as demonstrated by the on-note and the “in between” interpretations of graces 1 and 2.
It is noteworthy to mention that most pianists were aware of the their way of performing the grace note. S14 mentioned that she was performing the appoggiatura as she new it from different editions such as the original Paisiello aria: on the beat (Graces 1 and 2), or substituting the main note (Grace 3). Others mentioned pre-beat or on-beat performance. Not all pianists talked in these terms and some mentioned a different interpretation than was actually the case.

In the following analyses, grace duration was defined as the time interval between the onset of the grace note and the main note. We assumed a linear relationship between grace and bar duration. Figure 9 shows that this is a reasonable assumption. The slope β of this relation (as given by Equation 4) shows whether the grace note keeps a constant duration (β is not significantly different from 0), or whether it increases with bar duration (β is significantly larger than 0). The slope β_prop of the relation between grace proportion, which is defined as grace note IOI divided by the reference bar IOI, and bar duration (see Equations 6 and 7) shows whether the grace duration remains relationally invariant with bar duration (β_prop is not significantly different from 0), or whether the proportion increases or decreases with bar duration (β_prop is significantly larger or smaller than 0). If both relations do not show a significant fit, then the grace note duration does not vary with bar duration in a linear way.

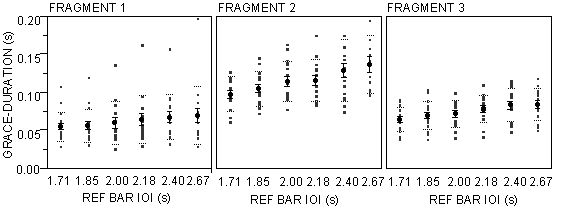
Figure 9. Individual values and average values of grace note duration per reference bar IOI category. The average values increase systematically and roughly linearly with reference bar IOI.

The reference bar IOI that corresponded to the duration category of the pre bar IOI was taken as bar duration measure (see section on Instructed vs. realized tempo). The fastest duration-category of 1.6 s had to be omitted from the analyses, since too few data points fell within its duration range.
In this analysis, the durations of the grace notes were compared with the duration of selected eighth notes from each fragment, over tempi. The comparison notes were the first accompaniment note (g of the G major chord) of the third measure of the first fragment (Figure 1a), and the fourth accompaniment note of the third measure of the second and third fragments (c of the a minor chord and d of the D7 chord, Figure 1b and 1c, respectively). These accompaniment notes were chosen on the grounds that they have a short duration (like a grace note), they do not fall within the pre bar (which would bias them to scale proportionally with tempo), and they are neither in the direct neighborhood of the grace note or part of the final ritard.
A repeated measures ANCOVA tested the effect of note type (grace note or eighth note), fragment (three levels), bar duration (continuous variable), and their interactions on the (grace or eighth) duration. A second repeated measures ANCOVA tested the same effects on (grace or eighth) proportion. Eighth proportion is defined as the eighth note IOI divided by the reference bar IOI.
The results showed significant main effects of note type, fragment and bar duration and significant interactions between note type and bar duration, and between note type and fragment on both note duration and note proportion (p < 0.005 for all effects). There was further a significant interaction between the effects of note type, fragment and bar duration on note duration (F (2,28) = 3.99, p < 0.05), but not on note proportion (F (2,28) = 1.87, p > 0.1).
Table 2 shows the details of these effects. It summarizes the mean grace note IOI (c’) and eighth note IOI (e’), mean grace note proportion (c’_prop) and eighth note proportion (e’_prop) and mean slope (β) of the relation between note IOI and reference bar IOI (D), and mean slope (β_prop) between note proportion and reference bar IOI (D). Averages are split per fragment when a significant effect of fragment was found in the ANCOVA. All reported means and mean slopes (β and β_prop) are significantly different from 0 (p < 0.01).
It can be seen that eighth notes were much longer than grace notes (effect of note type), that eighth notes scaled more than proportional with tempo, while grace notes scaled less than proportional (interaction between note type and bar duration). The duration of Grace 2 was larger than the duration of Grace 3 and Grace 1, while the eighth notes of the three fragments only differed slightly in duration (interaction between note type and fragment). Grace 2 varied more with bar duration than Grace 3 and Grace 1, though there was no significant difference in the proportional scaling between the grace notes. This means that when corrected for the mean grace duration, the duration of all three graces varied in the same way. There was no significant difference between the scaling of the three eighth notes (threefold interaction between note type, fragment and bar duration on note duration, but not on note proportion).

Table 2. Average duration of the grace (c’) and eighth note (e’) in seconds, their proportion of the bar duration (c'_prop and e'_prop) and their scaling behavior (β and β_prop)

When we turned to individual subjects, it became clear that the duration of grace notes and the scaling of the duration with tempo differed considerably between subjects. Table 3 shows that, for each fragment, there were subjects who performed the grace note with constant duration (first row), with less than relationally invariant duration (second row), with relationally invariant duration (third row), and sometimes even with more than relationally invariant duration (fourth row). There was an interesting preference for Grace 1 to be performed with constant duration (56% of the subjects) in contrast to the other two graces that mainly showed less than proportional scaling. There was also a small number of subjects who consistently performed the grace notes with relationally invariant (S3 and S9) or with constant duration (S2 and S4). S14 performed the grace notes with more than relational invariant scaling as in the case of the eighth notes. The duration of the grace notes in her performances was considerably longer than in any other performance. There was no clear relation between average grace duration and scaling behavior: graces that scaled proportionally were as short as graces that keep a constant duration and graces that scaled less than relationally invariant had longer duration.


Table 3. Number of subjects (N) and mean grace IOI (c’) in seconds for four types of
scaling behavior and for the three fragments.

To summarize, the durations of ornamental notes were different from durations of eighth notes in two respects: first, they were significantly shorter than eighth notes (the grace notes were less than a sixteenth note) and secondly, they showed different scaling behavior. All three grace notes scaled less than would be expected given relational invariance with bar duration, whilst the three eighth notes were found to scale more than would be expected given relational invariance.
In confirmation of Windsor et al., (2001), Grace 2 was performed on average almost twice as long as grace notes 1 and almost 1.5 times as long as Grace 3, though individual subjects showed marked differences in grace note duration.
The scaling behavior of the grace notes differed considerably between subjects. Instances were found of both constant as well as relational invariant grace note duration. The scaling behavior of grace notes was not bound to fragments, nor was it clearly bound to ornament categories. The subjects that were shown in the stolen time analyses to interpret the ornaments as grace notes showed constant duration, relationally invariant or less than relationally invariant scaling. The subjects that were shown to interpret Grace 2 as an on-note grace were not the only ones that performed Grace 2 with relationally invariant duration.
The pianists did not have correct intuitions on the scaling of duration with tempo changes. They did have a clear sense of the average duration of the grace notes and mentioned to perform the graces short, light, heavy, calm, melodic or pungent. These descriptions differed considerably between pianists, which might explain the diversity in performances found in the analyses. We say might, since, at this moment, it seems to involve too much speculation to make a sensible explanation of the grace note differences on these grounds. More qualitative research is needed at this point.

The success of the previous analyses provided the motivation for a model of grace note timing. Its characteristics are as follows: (a) The duration of a grace note scales linearly with tempo. (b) The insertion of a grace note only affects the timing of the preceding and following melody notes. (c) The timing of these notes is affected by stealing time from them. (d) The time stolen is a proportion of the grace note duration, irrespective of tempo.
The model consists of two parts. Its first part predicts the duration of the grace note and the second part determines how it is inserted and how it affects its direct context (see Figure 10). The model comprises four parameters: two for the grace duration and two for the grace position. These parameters depend on the type of grace note and the interpretation in the context of a musical fragment by the performer.
Instructed bar duration (D) is the tempo input to the first component of the model. The parameters are the grace duration at tempo 60 (c₆₀) and the slope of the linear relation between bar duration and grace note duration (β). The output is the predicted grace note duration (c’). This duration follows from Equations 8, which is the same as Equation 4 with the only difference that in the model the grace duration at tempo 60 is taken as parameter instead of the less meaningful intercept h. Similarly a difference in bar duration between the instructed bar IOI (D) and bar IOI at tempo 60 (D₆₀) is taken as tempo measure, instead of an absolute duration.^[6]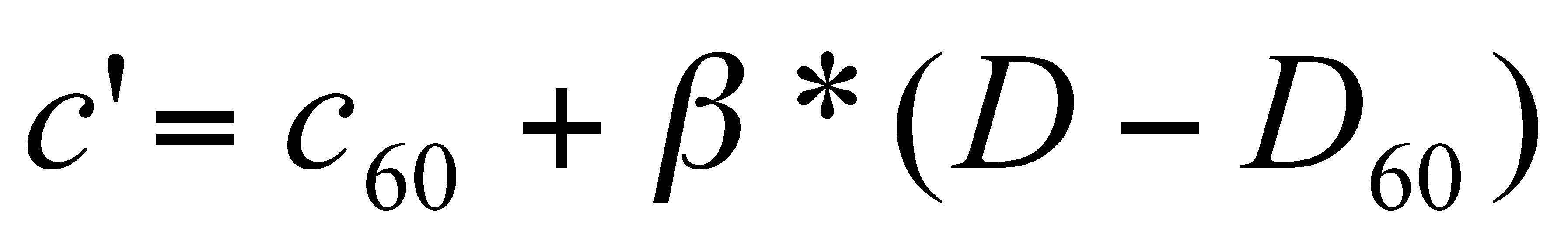

(8)

Equation 8 can be rewritten using s instead of the slope β. The use of s is more intuitive than the slope β, because it is 0 for grace notes with a duration that is constant with variations in bar duration and 1 for grace notes with a duration that varies proportional. Then Equation 8 becomes:

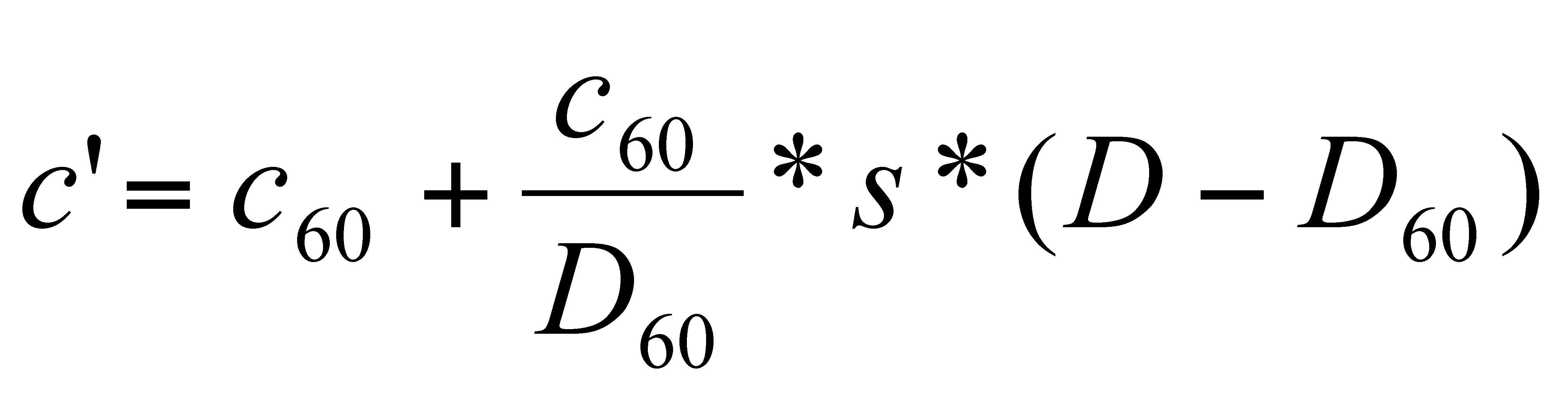
(9)

If we take tempo 60 as a reference, then this equation shows that the amount that the grace note increases with increments of the bar duration is a proportion (s) of the relative increase of D.
The input to the second component of the model consists of the grace duration (given by the first component of the model), and the duration of the previous and main note of the performance ‘without’ the grace note (a and b). The parameters of this component are previous stolen proportion (p) and main stolen proportion (m). The output is the predicted duration of the previous and main note of a performance ‘with’ grace note (a’ and b’). These durations follow from the Equations 10 and 11, which were derived from Equations 1 and 2:

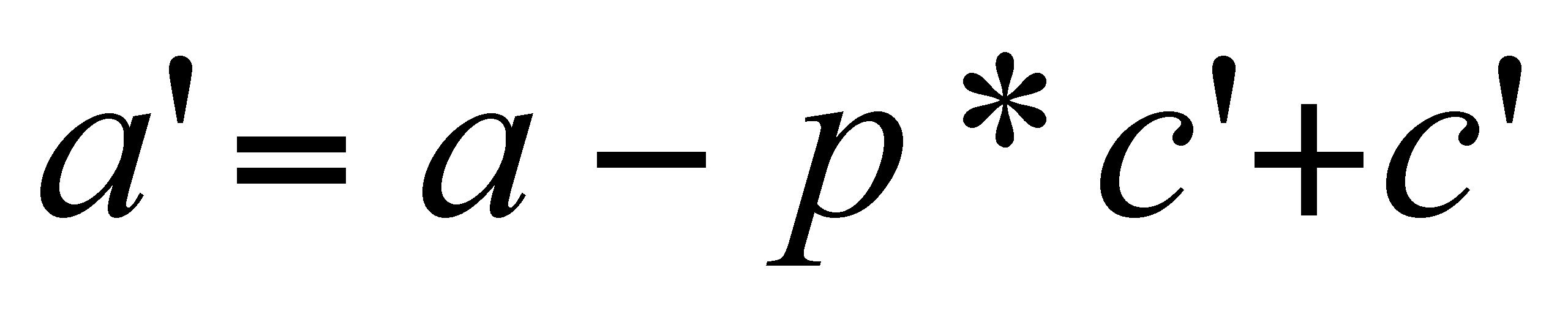
(10)

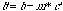
(11)

The model is simpler than the analyses in the sense that the p and m values do not depend on tempo, but are fixed per fragment and subject.


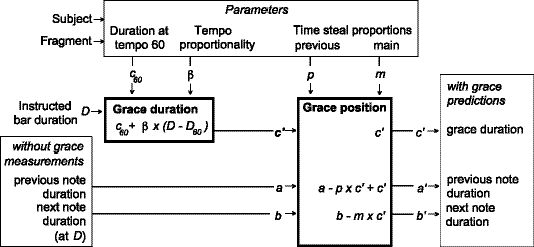
Figure 10. Grace note model. Overview of input, output and transformations (bold): c₆₀ is the duration of the grace note at tempo 60; β is the slope of linear relation between grace
note IOI and intro bar IOI; D is the intro bar IOI; p is the proportion stolen from the previous note; m is the proportion stolen from the main note; a is the previous IOI; b is the main IOI; c’ is the predicted grace note IOI; a’ is the predicted previous IOI; b’ is the predicted main IOI.

To validate the model, it was applied to the Beethoven data. Because the subjects were shown to interpret some grace notes differently, we choose to evaluate the model on a per-subject basis. The mean p, m, c’ at tempo 60, and β were calculated per fragment and per subject, which resulted in 48 measures of p, m, c’₆₀ and β. The resulting parameter values per subject and per fragment are as reported in the analyses, so for calculation of β, the slope of the relation between the grace note duration and the reference bar IOI, tempo 75 was excluded (see Tables 1 and 3 for a summary). These values were then used to predict the grace note duration (c’) and to adapt the duration of the previous IOI (a) and main IOI (b) to give room for the grace note.
Correlations between observed and predicted values were calculated per tempo and per fragment and were taken as a first indication for the goodness of fit of the prediction with the data. Table 4 reports the average correlations per fragment (averaged over tempi). The correlations were calculated per tempo condition and not over tempi, since the prediction of increasing durations of a’, b’ and c’ over tempi was seen as too easy a test for the model. Instead, these correlations indicate the goodness of the model to predict the relative differences between subjects. The correlations were all very high. For a’ and b’, it never came below 0.988 and for c’, it did not came below 0.847.

Table 4. Mean association and standard deviation over subjects between predicted and observed values of the previous IOI (a’), main IOI (b’), and grace IOI (c’) expressed with correlation (r) and relative prediction quality (q) for the three fragments.

This suggests a good fit, though we are not entirely satisfied with the use of correlations as the measure of fit. We aimed at accurate absolute predictions of time intervals, rather than accurate relative associations. We therefore tested the agreement between the predicted and observed data with a second measure. The relative prediction quality (q) of the model compares the variance of the error of the predicted (û) values with the variance of the observed values (see Equation 12).^[7]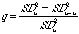

(12)

The measure q approaches 1 when the variance of the error between the predicted and observed measure is much smaller than the between subject variance of the observed data. This is the case when the error variance approaches 0 or is infinitely small with respect to the between subject variance. The prediction quality becomes 0 or negative when the variance of the difference between observed and predicted is equally large or larger than the between subject variance.
The q values were calculated per tempo of each fragment. Table 4 reports the average values for each predicted time interval and per fragment. The values show the same trend as the correlations, though they are more sensitive for differences between observed and predicted data. There is a very high q for the predicted main and previous duration for all tempi (all above 0.97) and a slightly lower error for the predicted values of the grace duration (though all still above 0.7). The lower q for the grace duration indicates that the grace duration is less strictly related to the instructed tempo than suggested by the model.
As a further validation, we compared the performance of the position component of the model with two simpler definitions. The first alternative is to take a and b as predictors of a’ and b’, which is a kind of base-line model that expects the duration of the previous and main note to be the same in the ‘with’ and ‘without’ grace note condition. The average values of q are given in Table 5. It can be seen that this base-line model predicts the two durations much less well than the position model proposed above.
A second alternative is to predict a’ and b’ to be a constant fraction of a and b, which suggests that the adaptation of the surrounding notes does not depend on the grace note duration, but depends on the duration of the notes themselves.
For the grace duration component, a similar alternative definition is possible: the grace note may primarily depend on the duration of the main note, and be a fixed proportion of the main note in the without condition.
Average values of the constant fractions were calculated separately per fragment of each subject and from these averages the durations of a’, b’ and c’ were predicted. The prediction quality was calculated per tempo and fragment condition. The average values of these are given in Table 5 (see alternative model).

Table 5. Relative prediction quality (q) for the different model definitions for the previous IOI (a’), main IOI (b’) and grace IOI (c’), and for the three fragments.

It can be seen that this simpler model predicts the durations less well than the full grace note timing model. So, the durations of the main and previous note in the ‘with’ condition do depend on the grace note duration and the grace note duration is better explained by two parameters, one providing an average and the other a scaling with tempo.
The last alternative model does, however, suggest an improvement of the full model, which is to make the grace note duration a function of the main note duration, not as a fixed proportion, but as a linear relation with default duration and a scaling factor.

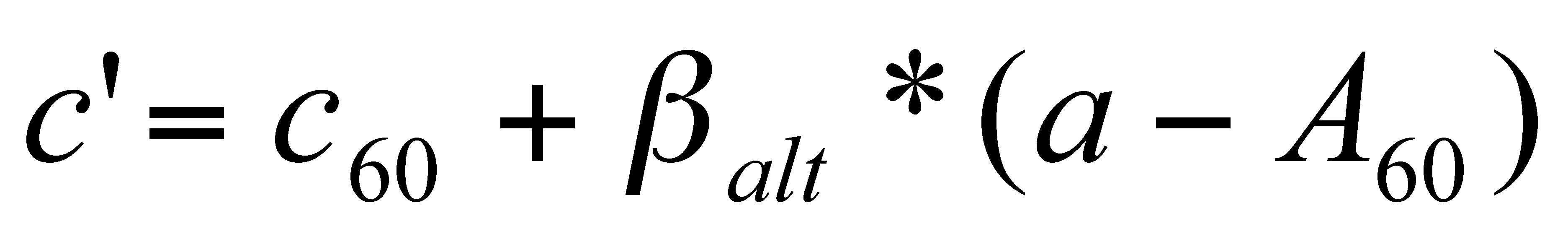
(13)

This adaptation of the grace note timing model improves q up to an average of 0.886 (see Table 5, last column). We may conclude that the grace note timing model predicts the grace duration and the previous and main duration well, especially when the grace note duration is taken as a function of the main note duration of the without condition, since predicted values closely approach the observed values.

The hypothesis was that the timing of a grace note depends on its type. It could be an on-note grace with all time stolen from the main note, a pre-note grace with all time stolen from the previous note, or an insertion grace with all duration of the grace note inserted. Grace 1 was predicted to be performed as either one of the three grace note types, depending on the taste of the performer. In any case, it would be a short grace note. Grace 2 was predicted to be performed as a long on-note grace. Grace 3 again could be performed as either one of the three case, most probably short, but it might also be performed as a long on-note grace, because of its suspension function.
The results showed significant differences between the grace notes of the three fragments, but these differences were less categorical than assumed in the predictions. The general trend was to perform all three grace notes (including Grace 2) as pre-note graces: most or all time was stolen from the previous note and little to no time was stolen from the main note.
Grace 2 differed from Grace 1 and 3, because on average less time was stolen from the previous note. It also differed from the other graces, because two subjects clearly changed their interpretation of the ornaments in fragment 2 with respect to fragments 1 and 3 from a pre-note interpretation to an on-note interpretation of the grace note.
Surprisingly, Grace 1 differed from the other graces by having a negative insertion proportion. This was related to a faster target bar in the ‘with’ condition than the ‘without’ condition. This might be due to a difference in phrasing between the ‘with’ and ‘without’ conditions, which was suggested by some of the pianists. While in the ‘without’ condition the melodic movement of fragment 1 gradually leads towards the high e of the post bar, in the ‘with’ condition, the movement is towards the grace note and the following main note. If the melodic movement is accompanied by an accelerando, this acceleration occurs earlier in the ‘with’ condition than in the ‘without’ condition.
The prediction for the scaling of grace note duration with tempo was that longer grace notes would scale in a relationally invariant manner with context duration similar to the ‘normal’ behavior of structural notes. Short grace notes would, however, scale less than relationally invariant or would even have invariant duration.
The results on this matter showed that, on average, all three graces scaled less than relationally invariant with tempo, irrespective of its average duration. The duration of the longer Grace 2 varied more with tempo than the shorter Graces 1 and 3, but the proportional scaling did not differ between the three graces.
Individual subjects showed instances of no scaling, relationally invariant scaling, and less or more than relationally invariant scaling for all three graces. There was no consistent relation between the average duration of the grace note and the proportionality of its scaling.
The differences between the subjects could well have been due to different ideas of the pianist regarding the grace notes. An explanation of this kind of the between subject differences fell outside the scope of this paper, but seems worthwhile for a qualitative follow-up study.
We proposed a grace note timing model, which states that the grace duration depends linearly on global bar duration, and that the addition of a grace note affects the timing of a musical piece only locally by shortening the notes preceding and following the grace note. The amount of shortening and the slope of the linear relation are parameters, the value of which depends on the performer and the fragment. The performance of this model was tested on the Beethoven data and showed a very high predictive power. This means that the subjects were very consistent (over tempi) in positioning the grace note with respect to the onset of the main note and scaling the duration of the grace note with tempo.
It is clear that this paper has contributed to our understanding of the grace note timing in this specific Beethoven piece, but some important issues have not been addressed. First of all, the question remains whether the subtle differences in grace note timing such as reported in the analyses of grace position and grace duration are perceivable. We used the grace note model to generate performances of the Beethoven fragments with grace notes timed in different ways. A web-demo was constructed to allow for easy exploration.^[8] It is possible to combine the timing data of structural notes of one pianist with the parameter settings for the grace note timing of another pianist. Exploration of different settings suggested a remarkable audibility of even small differences in grace note duration to the authors, such as between a grace note duration of 30 ms sounding very short and of 40 ms sounding just short. Two further clear observations were that an insertion grace is an unfamiliar way of executing grace notes, since the main note sounds too long in this interpretation, and the differences between on-note and pre-note interpretation as found in this paper are distinctive. These observations seem worthwhile to investigate further.
Secondly, there are certain relevant measures for grace note timing that have not been addressed. To give some further information: the articulation of the grace notes was generally legato with a small overlap between the grace note and the main note. On average, the grace note overlapped 10.2% of the main note IOI (SD 9.6%). The overlap between grace note and main note was always less than 50% of the main note duration, which indicates a legato performance of the grace note, but not an accaciatura interpretation in which the main note and grace note are intentionally performed together. The subject who performed the grace note with longest relative overlap also performed the rest of the fragment very legato. There were no systematic differences between the articulation of the pre-note graces and the on-note graces.
The asynchrony between the grace note and the accompaniment “main” note was in all cases positive with the grace note leading the accompaniment note. For the pre-note interpretations, the accompaniment note was performed more closely to the main note (average asynchrony was less than 1 ms) than to the grace note (average asynchrony 79 ms), while for the on-note interpretations the reverse was true: the accompaniment note was timed more closely to the grace note (average asynchrony 9.4 ms) than to the main note (average asynchrony -135 ms).
Finally, it is worth to pay attention to the dynamics of the grace and main notes as measured by the key-velocity. For Grace 1 and 3 the pattern is very clear: all subjects except S14 (who consistently interpreted the graces as an on-note grace) performed the grace notes with lower velocity than the main notes (the grace note had on average 90% of the main note velocity). For Grace 2, the differences in loudness are less pronounced and five subjects performed the grace note with higher velocity than the main note. Among these five subjects are the three subjects that interpreted Grace 2 as an on-note grace.
These short discussions of other aspects of grace note performance are certainly not conclusive. Exploration of the web-demo suggested that indeed there are important interdependencies between grace note duration, timing, and velocity that are related to the categorical differences indicated above, but are also more subtle than that. Further investigation seems worthwhile.

We conclude that we have confirmed the existence of two ornament categories that have distinct timing characteristics: the pre-note grace and the on-note grace, which are known as grace notes or appoggiatura performed before or on the beat in performance practice literature. We however also found consistent differences in the timing of a single ornament category, the pre-note grace as we call it. These differences could partly be related to the musical context in which the grace notes occurred and partly to the subject specific interpretation.
We further conclude that the grace notes in this study were timed differently from their structural counterparts. Stolen time was a consistent aspect of the grace notes, as well as less than relationally invariant scaling. It seems no coincidence that the duration of a grace note is not specified in the musical score, while other notes receive a written notation that is related to their idealized proportional duration.

Bach, C. P. E. (1780, 1978). Versuch über die wahre Art das Clavier zu spielen. Leipzig: Breitkopf & Haertel Musikverlag.

Clarke, E. (1999). Rhythm and Timing in Music. In D. Deutsch (Ed.), Psychology of Music (pp. 473-500). New York: Academic Press.

Desain, P., & Honing, H. (1994). Does expressive timing in music performance scale proportionally with tempo? Psychological Research, 56, 285-292.

Donington , R. (1963, 1989). The interpretation of early music. New rev. ed. London: Faber and Faber.

Donington, R. (2001). Ornaments. In S. Sadie & J. Tyrell (ed.) The New Grove: dictionary of music and musicians. London: Grove.

Friberg, A., & Sundström, J. (1999). Jazz Drummers' Swing Ratio in Relation to Tempo. Published online as Acoustical Society of America ASA/EAA/DAGA '99 Meeting Lay Language Papers.

Geminiani, F. (1749, 1969). A treatise of good taste in the art of music. New York : Da Capo Press.

Gentner, D. R. (1987). Timing of Skilled Motor Performance: Tests of the Proportional Duration Model. Psychological Review, 94 (2), 255-276.

Heijink, H., Desain, P., Honing, H., & Windsor, L. (2000) Make me a match: An evaluation of different approaches to score-performance matching. Computer Music Journal. 24 (1), 43-56.

Honing, H. (1990). POCO: an environment for analysing, modifying, and generating expression in music. In Proceedings of the 1990 International Computer Music Conference (pp. 364-368). San Francisco: Computer Music Association.

Neumann, F. (1986). Ornamentation and Improvisation in Mozart. Princeton & Oxford: Princeton University Press.

Neumann, F. (1993). Performance practices of the seventeenth and eighteenth centuries. New York: Schirmer Books.

Parncutt, R. (1994). A perceptual Model of Pulse Salience and Metrical Accent in Musical Rhythms. Music Perception, 11 (4), 409-464.

Quantz, J. (1752, 1992). Versuch einer Anweisung, die Flöte traversiere zu spielen. München: Deutscher Taschenbuch Verlag; Kassel: Baerenreiter

Repp, B. H. (1994). Relational invariance of expressive microstructure across global tempo changes in music performance: An exploratory study. Psychological Research, 56, 269-284.

Schmidt, R. A. (1985). The search for invariance in skilled movement behavior. Research Quarterly for Exercise and Sport, 56 (2), 188-200.

Sundberg, J., A. Friberg & Frydén, L. (1991). Common Secrets of Musicians and Listeners: An analysis-by-synthesis Study of Musical Performance. In P. Howell, R. West, & I. Cross (Eds.), Representing Musical Structure (pp. 161-197). London: Academic Press.

Windsor, W. L., Desain, P., Aarts, R., Heijink, H., & Timmers, R. (2001). The timing of grace notes in skilled musical performance at different tempi: a case study. Psychology of Music, 29, 149-169.

This work was undertaken as part of the ‘Music, Mind Machine’ project at the Nijmegen Institute for Cognition and Information (NICI) which is funded through a Pionier grant from the Netherlands Organization for Scientific Research. The authors would like to express thanks to Paul Trilsbeek for doing the studio work, Yvonne Schouten (Mathematical Psychology, NICI) for her assistance with collecting the experimental data and to Dick Willems and Eric Maris (Mathematical Psychology, NICI) for their assistance with some of the statistical issues in this study. Especial thanks to all pianists who participated in this study for their excellent playing and to Caroline Palmer, Richard Parncutt and an anonymous reviewer for their helpful comments.

^[1] We will return to this issue in the discussion and provide some evidence in favor of the assumption.
^[2] This Beethoven theme was also used in Desain & Honing (1994) and Windsor et al., (2001).

^[3] Grace 1, 2 and 3 are grace note 1, 2 and 5 in Windsor et al., (2001).

^[4] The average deviation of the pre bar duration from the instructed bar duration is maximally – 4.3%, which is the mean deviation for Grace 2, instructed bar of 2.67 S, which shows the largest discrepancy. Largest individual deviations that occur do not exceed 12%.
^[5] The faster tempo of the next note is enlarged, since it concerns the local tempo of a sixteenth note. This means that the absolute difference between “with” and “without” does not need to be large to give a considerable difference in local tempo.
^[6] Equation 8 can be rewritten as Equation 4 if one substitutes d + β * 2 for c₆₀.
^[7] This measure of relative prediction quality was suggested by Eric Maris, mathematical psychology, NICI, University of Nijmegen.
^[8] See <https://www.nici.kun.nl/mmm/> under the header “Demo’s”